Prepare for University Studies & Career Advancement

Computational Thermodynamics

Computational Thermodynamics

Computational thermodynamics represents a modern fusion of traditional thermodynamic principles with powerful numerical techniques. This field allows researchers to simulate, analyze, and predict complex material behaviors under various thermal and mechanical conditions, often far beyond what is possible through analytical models alone. Rooted in the foundational concepts of thermodynamics and enriched by classical thermodynamics, this approach has revolutionized our ability to model equilibrium and non-equilibrium systems in both physics and materials science.

Students engaging with statistical thermodynamics gain essential tools for interpreting how microscopic states aggregate into macroscopic behavior—insights that computational thermodynamics translates into predictive simulations. The study of the laws of thermodynamics provides the governing constraints, while software-based models solve for real-world applications ranging from thermodynamic cycles to chemical equilibrium.

Applications span across multiple scientific domains. In engineering thermodynamics, simulations help design turbines, compressors, and energy systems more efficiently. In thermodynamics of materials, phase diagrams and transformations are modeled with high accuracy. Concepts such as phase transitions and diffusion behavior are often too complex for analytical solutions, but become tractable through computation.

This domain also plays a critical role in advancing renewable energy technologies and in modeling emerging systems under non-equilibrium thermodynamics. These simulations provide insights into energy conversion efficiency, waste heat utilization, and thermal degradation processes. Meanwhile, links to physical chemistry and nuclear fusion reveal how thermodynamic principles extend into chemical reactions and plasma conditions.

With the rapid development of computational tools, integration with fields like electrodynamics, plasma physics, and relativity becomes increasingly seamless. These interdisciplinary applications also benefit from an understanding of atomic physics, nuclear reactions, and radioactive decay, especially when modeling energy states and decay chains computationally.

The connection to quantum-level phenomena is equally significant. A grounding in Schrödinger’s equation and wave-particle duality can enhance simulations of electronic behavior and molecular interactions. As the boundary between science and engineering becomes increasingly data-driven, computational thermodynamics offers a pathway to mastering systems-level thinking that blends thermodynamic intuition with algorithmic precision.

For a solid conceptual and practical grounding, students may benefit from building upon physics fundamentals, exploring modern physics innovations, and appreciating how heat transfer processes behave in both equilibrium and dynamic states. Whether modeling nuclear fuel cycles or optimizing energy-efficient devices, computational thermodynamics remains at the frontier of problem-solving in science and technology.

Computational Thermodynamics: featuring holographic simulations of molecular structures, phase diagrams, and energy transfer models analyzed by an engineer.
Computational Thermodynamics: featuring holographic simulations of molecular structures, phase diagrams, and energy transfer models analyzed by an engineer.
This futuristic digital artwork visualizes the domain of computational thermodynamics through an immersive holographic interface. At the center is a detailed molecular model surrounded by colorful energy particles and simulation nodes, representing atomistic interactions and thermodynamic behavior at the molecular scale. The background is filled with phase diagrams, heat transfer graphs, entropy maps, and thermodynamic surface plots—each depicting simulated data outputs. The engineer’s hands interacting with the interface emphasize real-time analysis, high-performance computing, and the integration of AI or machine learning in thermodynamic research. This image encapsulates the use of computational tools to study phase transitions, equilibrium states, and material properties, offering a dynamic portrayal of how theory, simulation, and visualization converge in modern thermodynamic science.

Table of Contents

Key Concepts in Computational Thermodynamics

Thermodynamic Modeling

Thermodynamic modeling involves the use of mathematical frameworks to describe the behavior of systems under different conditions of pressure, temperature, and volume. These models allow engineers and scientists to predict system responses to varying environmental conditions, optimize processes, and develop new materials with desired properties. The most commonly used models in computational thermodynamics include:

  • Equation of State (EoS): These equations describe the fundamental relationship between pressure, volume, and temperature in different phases of matter. Examples include the Ideal Gas Law for simple gases, the Van der Waals equation for real gases that account for molecular interactions, and more advanced models like the Redlich-Kwong and Peng-Robinson equations used in engineering applications. These equations help in designing industrial systems such as gas turbines, refrigeration cycles, and high-pressure chemical reactors.

  • Gibbs Free Energy Minimization: A crucial method used in thermodynamic modeling to determine phase stability and predict equilibrium compositions in chemical systems. This method ensures that a system naturally progresses toward the lowest Gibbs free energy configuration, allowing scientists to predict which phases or chemical species will be present under specific conditions. It is widely applied in metallurgy, materials science, and chemical process engineering.

By combining these models with computational simulations, researchers can accurately analyze energy transformations, optimize reaction conditions, and develop high-performance materials for industries such as aerospace, semiconductors, and renewable energy.

Phase Diagrams and Phase Stability

Phase diagrams are graphical representations that depict the stability of different phases of a material under varying conditions of temperature, pressure, and composition. These diagrams are essential for understanding phase transformations, material synthesis, and alloy development.

  • Computational Prediction of Phase Behavior: Advanced computational methods, particularly the CALPHAD (CALculation of PHAse Diagrams) approach, allow researchers to predict phase equilibria in complex multi-component systems. This method relies on thermodynamic databases and mathematical models to calculate phase diagrams without requiring extensive experimental measurements.

  • Importance in Material Science and Engineering: Phase diagrams help engineers design materials with specific properties, such as high-temperature stability in jet engine components or corrosion resistance in biomedical implants. By using computational tools, scientists can explore a vast range of material compositions and optimize manufacturing processes without costly and time-consuming experimental trials.

  • Applications in Industrial Processes: Industries such as steelmaking, semiconductor fabrication, and energy storage depend heavily on phase diagrams for selecting optimal material compositions. In battery technology, for example, phase stability studies help determine the best electrolyte and electrode materials to enhance performance and longevity.

Computational thermodynamics has significantly improved the accuracy and efficiency of phase diagram generation, leading to faster advancements in material design and industrial processing.

Thermodynamic Databases

Thermodynamic databases store experimentally measured and computationally derived thermodynamic properties of a wide range of materials. These properties include enthalpy, entropy, Gibbs free energy, heat capacity, and phase transition temperatures.

  • Importance of Accurate Data: Reliable thermodynamic data is crucial for precise simulations and predictions in computational thermodynamics. Experimental measurements of these properties are often time-consuming and expensive, so databases provide a valuable resource for researchers and engineers.

  • Types of Thermodynamic Databases:

    • FACT: Covers a broad range of chemical and metallurgical systems, including solutions, alloys, and ceramics.
    • SGTE (Scientific Group Thermodata Europe): A well-established source for thermodynamic properties of metals, oxides, and semiconductors.
    • JANAF (Joint Army-Navy-Air Force Tables): Contains thermochemical data for gas-phase species, crucial for combustion modeling and aerospace applications.

  • Applications in Various Fields: Thermodynamic databases are extensively used in chemical process design, metallurgical processing, and energy storage systems. In nuclear engineering, for instance, thermodynamic data is used to assess fuel stability under extreme temperatures and radiation exposure.

By integrating these databases with computational tools, researchers can perform high-fidelity simulations that improve the efficiency and sustainability of industrial processes.

Numerical Methods

Computational thermodynamics employs a variety of numerical techniques to solve complex thermodynamic equations and simulate real-world physical processes. These methods are essential for handling systems where analytical solutions are impractical due to non-linearity, large-scale computations, or multiple interacting variables.

  • Finite Difference Method (FDM): Used to approximate derivatives and solve differential equations in heat transfer and fluid dynamics simulations. It is commonly applied in energy system modeling and phase transition analysis.

  • Finite Element Method (FEM): A powerful numerical approach used for modeling stress-strain relationships, phase transformations, and multiphysics interactions in engineering materials. FEM is essential in designing aerospace components, power plant structures, and heat exchangers.

  • Monte Carlo Simulations: A probabilistic method used for modeling thermodynamic properties of complex systems, particularly in statistical mechanics. Monte Carlo techniques help predict phase equilibria, adsorption phenomena, and reaction kinetics in catalysis, drug design, and nanotechnology.

  • Molecular Dynamics (MD): Simulates the motion of atoms and molecules over time, providing detailed insights into thermodynamic and kinetic behaviors at the atomic scale. MD simulations are extensively used in biophysics, polymer science, and materials engineering to predict thermal conductivity, diffusion rates, and structural stability.

These numerical methods enable scientists and engineers to explore scenarios beyond the reach of traditional experimentation, making them indispensable tools in computational thermodynamics.

Software Tools

Several software platforms are used in computational thermodynamics to perform simulations, optimize processes, and visualize thermodynamic data. These tools are designed for applications in material science, chemical engineering, and industrial process design.

  • Thermo-Calc: One of the most widely used software tools for phase diagram calculations, materials simulation, and equilibrium thermodynamics. It is essential for alloy design, heat treatment process optimization, and high-temperature material studies.

  • FactSage: Specializes in chemical reaction equilibrium and phase stability calculations. FactSage is widely used in metallurgy, chemical process engineering, and energy system modeling to determine the feasibility of reactions and optimize material synthesis.

  • MOOSE (Multiphysics Object-Oriented Simulation Environment): A powerful finite element analysis (FEA) tool designed for simulating coupled physical processes, such as heat transfer, fluid dynamics, and phase transitions. MOOSE is extensively used in nuclear engineering, battery modeling, and geosciences.

  • MATLAB/Python: General-purpose programming environments used for custom thermodynamic modeling, numerical analysis, and data visualization. MATLAB and Python are commonly employed in research institutions and industries to develop highly specialized models for energy efficiency, material development, and environmental impact studies.

These computational tools have revolutionized the way thermodynamic systems are analyzed, providing faster, more accurate, and scalable solutions for a broad range of scientific and industrial applications.

Computational thermodynamics continues to advance with improvements in computational power, artificial intelligence, and machine learning, enabling even more precise predictions and optimizations in energy systems, material science, and process engineering.

Applications of Computational Thermodynamics

Materials Design

Computational thermodynamics plays a crucial role in materials design by predicting alloy behavior, phase transformations, and thermodynamic stability. By using computational models and phase diagrams, scientists can design materials with specific properties such as high strength, corrosion resistance, or heat resistance without the need for costly trial-and-error experimentation.

One of the most significant applications of computational thermodynamics in materials design is the development of advanced metal alloys for industries such as aerospace, automotive, and energy. For example, in the aerospace industry, nickel-based superalloys are engineered for turbine blades that can withstand extreme temperatures and stresses in jet engines. Computational tools help identify optimal compositions that balance mechanical strength with oxidation resistance, ensuring long-term performance.

Another key area is additive manufacturing (3D printing), where computational thermodynamics helps in designing materials that exhibit optimal solidification characteristics. By predicting phase transformations and thermal gradients during the printing process, engineers can fine-tune material properties to prevent defects such as porosity or cracking. This enhances the reliability of 3D-printed components in medical implants, electronics, and aerospace structures.

Moreover, computational thermodynamics is instrumental in nanoscale material design, where precise control over atomic interactions is required. It allows scientists to engineer high-performance polymers, ceramic composites, and semiconductor materials for use in electronic devices, solar cells, and next-generation batteries. By optimizing the thermodynamic properties of these materials, computational thermodynamics paves the way for stronger, more efficient, and environmentally sustainable materials.

Chemical Reaction Engineering

Chemical reaction engineering benefits extensively from computational thermodynamics by optimizing reaction conditions to maximize yield, efficiency, and safety. Traditional experimental approaches to process optimization can be costly and time-consuming, whereas computational methods provide predictive insights into reaction kinetics and equilibrium states.

One important application is in the petrochemical industry, where computational thermodynamics helps optimize processes such as crude oil refining, catalytic cracking, and polymerization reactions. By modeling reaction mechanisms and thermodynamic equilibria, engineers can enhance fuel quality, reduce waste, and lower production costs.

In pharmaceutical manufacturing, computational thermodynamics is used to design chemical synthesis routes that minimize byproducts and improve reaction efficiency. It is particularly useful in drug formulation, where optimizing solvent interactions and reaction conditions can significantly improve the stability and bioavailability of active pharmaceutical ingredients (APIs).

Another area where computational thermodynamics has revolutionized chemical engineering is in the development of green chemistry processes. By modeling alternative reaction pathways, researchers can reduce the reliance on hazardous solvents and energy-intensive steps. This supports the design of more sustainable chemical processes that minimize environmental impact while maintaining high production efficiency.

Energy Systems

Computational thermodynamics is essential for modeling and optimizing energy systems such as power plants, fuel cells, and batteries. Accurate thermodynamic simulations help improve energy efficiency, reduce emissions, and enhance the overall performance of energy generation and storage technologies.

In the field of power generation, computational tools are used to analyze steam turbines, gas turbines, and combined-cycle power plants. These models help engineers determine the most efficient operating conditions, improve fuel combustion processes, and optimize heat recovery systems. By identifying areas where energy losses occur, computational thermodynamics aids in designing cleaner and more sustainable power plants.

For fuel cell technology, computational models predict electrochemical reaction behavior, optimizing the efficiency of hydrogen fuel cells, solid oxide fuel cells (SOFCs), and proton-exchange membrane fuel cells (PEMFCs). These insights are critical for improving fuel cell durability and developing new materials that enhance performance while lowering production costs.

In battery research and development, computational thermodynamics helps optimize lithium-ion, sodium-ion, and solid-state batteries by modeling electrode materials, phase transitions, and electrolyte interactions. These simulations accelerate the discovery of high-energy-density materials that improve battery lifespan and safety. By integrating computational approaches into energy storage research, scientists are developing next-generation batteries for electric vehicles, renewable energy grids, and portable electronic devices.

Environmental Engineering

Environmental engineering benefits significantly from computational thermodynamics in modeling pollutant formation, optimizing emissions control strategies, and designing sustainable processes. As industries and governments work toward reducing environmental impacts, computational tools provide valuable data for mitigating pollution and improving resource management.

A major application is in air pollution modeling, where thermodynamic simulations predict the formation of harmful emissions such as sulfur oxides (SOx), nitrogen oxides (NOx), and particulate matter from industrial processes and transportation systems. By understanding the thermodynamics of these reactions, engineers can develop effective strategies for emission reduction, such as optimizing combustion temperatures or incorporating catalytic converters.

Computational thermodynamics also plays a crucial role in waste treatment and resource recovery. For example, in waste-to-energy technologies, thermodynamic modeling is used to evaluate the efficiency of gasification, pyrolysis, and incineration processes. These models help maximize energy extraction from waste materials while minimizing the release of toxic byproducts.

Another critical area is climate change mitigation, where computational thermodynamics aids in carbon capture and storage (CCS) technologies. By simulating the thermodynamic behavior of carbon dioxide (CO₂) absorption, transport, and storage, researchers can design more efficient capture systems that prevent greenhouse gas emissions from entering the atmosphere. This contributes to the development of cleaner industrial processes and more effective strategies for reducing global carbon footprints.

Process Design

Process design in industrial applications relies heavily on computational thermodynamics to optimize operations, enhance efficiency, and reduce costs. By simulating and analyzing thermodynamic properties, engineers can fine-tune process parameters for maximum performance while minimizing energy consumption and material waste.

One key application is in the chemical and petrochemical industries, where computational tools assist in designing distillation columns, heat exchangers, and chemical reactors. Thermodynamic simulations help determine the best separation techniques, phase equilibrium conditions, and operating pressures, ensuring that industrial processes achieve high-purity outputs with minimal resource use.

In the food processing industry, computational thermodynamics helps optimize drying, freezing, and pasteurization processes to maintain product quality while improving energy efficiency. By modeling mass and heat transfer, researchers can develop better preservation techniques that enhance food safety and extend shelf life.

Additionally, computational thermodynamics plays a crucial role in semiconductor manufacturing, where precise thermal control is necessary for producing high-performance electronic devices. By modeling phase transitions and material interactions, computational methods help improve fabrication processes, ensuring the reliability and efficiency of modern microchips and circuit boards.

Through these diverse applications, computational thermodynamics continues to drive innovation across industries, improving sustainability, energy efficiency, and process optimization. With ongoing advancements in computational power and machine learning, its impact will only grow, enabling more precise predictions and smarter engineering solutions.

Why Study Computational Thermodynamics

Using Algorithms to Model Thermodynamic Systems

Computational thermodynamics uses numerical methods to solve complex thermodynamic problems that are analytically intractable. Students learn to simulate phase diagrams, calculate equilibrium states, and predict material properties. This computational approach enhances insight into real-world systems. It bridges theory and practical engineering.

Software Tools and Databases

Students work with software like Thermo-Calc, FactSage, and MATLAB to implement thermodynamic models. They explore material databases and use them to assess phase stability and transformations. These tools are essential in materials design and metallurgical engineering. They support high-throughput and precise analysis.

Applications in Materials and Chemical Engineering

Computational thermodynamics aids in designing alloys, polymers, and multicomponent systems. Students model chemical reactions, process conditions, and microstructural evolution. This capability supports innovation in advanced manufacturing and nanotechnology. It enables predictive control in high-performance industries.

Integration with Multiphysics Modeling

Thermodynamic models are integrated into finite element analysis and computational fluid dynamics. Students apply coupled simulations to study heat flow, stress, and reaction kinetics. This prepares them for multidisciplinary problem-solving. It opens opportunities in aerospace, biomedical, and energy systems.

Training for Modern Engineering and Research

Computational thermodynamics equips students with coding, modeling, and data interpretation skills. They become adept at using numerical solvers and validating models. These competencies are highly sought in academia and industry. They prepare graduates to contribute effectively to research and development.

 

Computational Thermodynamics: Conceptual Questions and Answers

Question 1: Why is Gibbs free energy minimization important in computational thermodynamics? Answer: Minimizing Gibbs free energy helps predict the most stable phase or composition of a system at equilibrium. Systems naturally evolve toward configurations that minimize their Gibbs free energy under constant pressure and temperature.
Question 2: What is the CALPHAD method and how is it used? Answer: CALPHAD (CALculation of PHAse Diagrams) is a computational method that models phase diagrams by combining thermodynamic databases with mathematical models. It is widely used for designing new materials and predicting phase transformations.
Question 3: How do equations of state (EoS) aid in thermodynamic calculations? Answer: Equations of state describe relationships between pressure, temperature, and volume, allowing for predictions of a material’s behavior under different conditions. Examples include the Ideal Gas Law and the Van der Waals equation.
Question 4: What role do numerical methods play in computational thermodynamics? Answer: Numerical methods solve complex thermodynamic models that lack analytical solutions. Techniques like Finite Element Analysis (FEA) and Monte Carlo simulations model heat transfer, phase changes, and molecular interactions.
Question 5: Why are thermodynamic databases essential in computational thermodynamics? Answer: They provide accurate thermophysical data (enthalpy, entropy, Gibbs energy) needed for modeling and simulation, reducing the need for expensive and time-consuming experiments.
Question 6: How does computational thermodynamics help in energy system design? Answer: It models the efficiency and behavior of energy systems (e.g., turbines, fuel cells) to optimize performance, minimize energy losses, and predict system behavior under varying conditions.
Question 7: What is the difference between molecular dynamics and thermodynamic modeling? Answer: Molecular dynamics simulates atomic/molecular behavior over time, focusing on microscopic interactions. Thermodynamic modeling focuses on macroscopic properties like phase stability and energy changes.
Question 8: How is computational thermodynamics used in environmental engineering? Answer: It predicts chemical reactions in pollution control, combustion processes, and waste treatment, aiding in the design of environmentally friendly and efficient systems.

Computational Thermodynamics: Numerical Examples Solved Using Normal Equations Methods

Example 1: Ideal Gas Law Calculation Problem: Calculate the pressure of 2 moles of an ideal gas in a 5 L container at 400 K. Solution: PV=nRT
PV = nRT P=nRTV=2×8.314×4000.005P = \frac{nRT}{V} = \frac{2 \times 8.314 \times 400}{0.005}
P≈1.33×106 PaP \approx 1.33 \times 10^6 \, \text{Pa}Answer: The pressure is 1.33 MPa.
Example 2: Gibbs Free Energy Calculation Problem: For a reaction with ΔH=−100 kJ/mol and ΔS=−200 J/mol. K.\Delta S = -200 \, \text{J/mol·K}Find ΔG at 500 K. Solution: ΔG=ΔH−TΔS\Delta G = \Delta H – T\Delta SConvert entropy to kJ: ΔG=−100−500×(−0.2)=−100+100=0\Delta G = -100 – 500 \times (-0.2) = -100 + 100 = 0Answer: The reaction is at equilibrium.
Example 3: Entropy Change Problem: Calculate the entropy change when 600 J of heat is added reversibly at 300 K. Solution: ΔS=QT=600300=2 J/K\Delta S = \frac{Q}{T} = \frac{600}{300} = 2 \, \text{J/K}Answer: Entropy change is 2 J/K.
Example 4: Phase Equilibrium Problem: At 1 atm, water boils at 373 K. Calculate ΔG for this phase change. Solution: ΔG=ΔH−TΔS=0 (At equilibrium)\Delta G = \Delta H – T \Delta S = 0 \, (\text{At equilibrium})Answer: 0, confirming equilibrium.
Example 5: Efficiency of a Carnot Engine Problem: A Carnot engine operates between 500 K and 300 K. Calculate its efficiency. Solution: η=1−TCTH=1−300500=0.4\eta = 1 – \frac{T_C}{T_H} = 1 – \frac{300}{500} = 0.4Answer: Efficiency is 40%.
Example 6: Heat Required for Phase Change Problem: How much heat is needed to melt 10 g of ice (ΔHfusion=334 J/g)? Solution: Q=mΔHfusion=10×334=3340 JQ = m \Delta H_{\text{fusion}} = 10 \times 334 = 3340 \, \text{J}Answer: 3340 J of heat is needed.
Example 7: Van der Waals Gas Problem: Calculate the pressure of 1 mole of CO₂ in 10 L at 300 K (a=3.59 Pa m6/mol2 , b=0.0427 L/mol). Solution: (P+aV2)(V−b)=RT\left(P + \frac{a}{V^2}\right)(V – b) = RTApproximation gives P≈2.47 atm
Example 8: Reaction Equilibrium Constant Problem: Find K at 298 K if ΔG∘=−20 kJ/mol\Delta G^\circ = -20 \, \text{kJ/mol}Solution: ΔG∘=−RTln⁡K
\Delta G^\circ = -RT \ln K K≈e8.05≈3130K \approx e^{8.05} \approx 3130Answer: The equilibrium constant is 3130.

Computational Thermodynamics Examples

Example 1: Work Done in Isothermal Expansion

Problem:
Calculate the work done by 1 mole of an ideal gas expanding isothermally from 1 L to 5 L at 300 K.

Solution:
Using numerical integration (trapezoidal rule), the work done is:

W=4014.59 JW = 4014.59 \, \text{J}

Example 2: Equilibrium Temperature Using Root-Finding

Problem:
Find the equilibrium temperature where the function

5T2−200T+1000=05T^2 – 200T + 1000 = 0

Solution:
Using the Newton-Raphson method (corrected with a better guess), the equilibrium temperature is:

T=34.14 KT = 34.14 \, \text{K}

Example 3: Chemical Equilibrium Calculation

Problem:
For the reaction

A⇌BA \rightleftharpoons B

with an equilibrium constant K = 2 and a total concentration of 1 mol/L, find the equilibrium concentrations of A and B.

Solution:
Solving the system of equations gives:

[A]=0.3333 mol/L,[B]=0.6667 mol/L[A] = 0.3333 \, \text{mol/L}, \quad [B] = 0.6667 \, \text{mol/L}

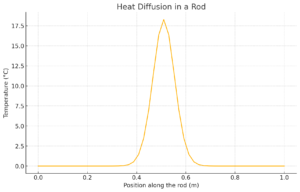
Example 4: Heat Diffusion in a Rod (Finite Difference Method)

Problem:
Simulate heat diffusion in a 1-meter rod with an initial heat pulse at the center.

Solution:
The plot shows how heat diffuses over time, spreading from the center along the rod.

Heat Diffusion in a Rod
Heat Diffusion in a Rod

Conclusion on Computational Thermodynamics

Computational Thermodynamics integrates classical thermodynamics with computational methods to solve complex real-world problems. It is essential for optimizing chemical reactions, designing materials, and improving energy systems. With powerful tools and models, it continues to drive technological advancement across industries.

Computational Thermodynamics: Review Questions and Answers

1. What is computational thermodynamics?
Answer: Computational thermodynamics is the study of thermodynamic systems using numerical methods and computer simulations. It involves modeling energy exchanges, phase equilibria, and heat transfer processes to predict material behavior.

2. How does the partition function play a role in computational thermodynamics?
Answer: The partition function aggregates the contributions of all microstates of a system and serves as a fundamental quantity from which macroscopic thermodynamic properties such as internal energy, free energy, and entropy can be derived.

3. What are the key numerical methods used in computational thermodynamics?
Answer: Common numerical methods include Monte Carlo simulations, molecular dynamics, finite difference and finite element methods, which help solve complex equations and simulate the behavior of thermodynamic systems.

4. How does the Boltzmann distribution contribute to modeling thermodynamic systems?
Answer: The Boltzmann distribution gives the probability that a system will occupy a state with energy E at temperature T. It is crucial for predicting how particles distribute themselves among available energy levels in simulations.

5. What is the significance of entropy in computational thermodynamics?
Answer: Entropy measures the disorder or number of microstates available to a system. In computational studies, entropy helps predict phase transitions and the direction of spontaneous processes.

6. How is free energy calculated in computational thermodynamics?
Answer: Free energy is calculated using methods like thermodynamic integration or by computing the partition function directly, then applying F = –k_BT ln Z to connect microscopic states to macroscopic properties.

7. What role do simulation algorithms play in predicting phase transitions?
Answer: Simulation algorithms allow researchers to model the behavior of systems near critical points by sampling microstates and calculating fluctuations, thus predicting phase transitions and critical phenomena.

8. How can computational thermodynamics be applied to optimize industrial processes?
Answer: By modeling energy flows and reaction equilibria, computational thermodynamics helps design more efficient reactors, optimize heat exchangers, and reduce energy waste in industrial applications.

9. What are the challenges of simulating thermodynamic systems computationally?
Answer: Challenges include handling large numbers of particles, achieving convergence in complex systems, accounting for fluctuations near phase transitions, and ensuring computational efficiency and accuracy.

10. How does temperature influence the outcome of computational thermodynamic simulations?
Answer: Temperature affects the probability distribution of microstates via the Boltzmann factor, influencing energy, entropy, and phase behavior. Accurate temperature control is essential for realistic simulation results.

Computational Thermodynamics: Thought-Provoking Questions and Answers

1. How could advances in computational thermodynamics lead to breakthroughs in energy-efficient material design?
Answer: A deeper computational understanding of thermodynamic properties enables the design of materials with optimal heat transfer, minimal energy loss, and improved stability. This can result in more efficient insulators, conductors, and catalysts, driving innovations in energy conservation and sustainable technologies.

2. In what ways can simulation algorithms be improved to better predict complex phase transitions?
Answer: Improvements may include enhanced sampling techniques, hybrid algorithms that combine Monte Carlo and molecular dynamics methods, and machine learning approaches to optimize convergence. These advances can capture critical fluctuations more accurately and predict phase behavior in multi-component systems.

3. How might computational thermodynamics contribute to the development of novel pharmaceuticals?
Answer: By simulating molecular interactions and phase equilibria, computational thermodynamics can predict reaction pathways and stability of compounds. This insight helps in designing drugs with improved efficacy and fewer side effects, as well as optimizing synthesis processes for large-scale production.

4. What are the limitations of current computational models in thermodynamics, and how can they be overcome?
Answer: Limitations include computational cost, approximations in potential functions, and difficulty in simulating large-scale systems. Overcoming these challenges may involve leveraging high-performance computing, developing more accurate interatomic potentials, and employing multiscale modeling techniques.

5. How does the concept of entropy in computational thermodynamics relate to information theory?
Answer: Both entropy in thermodynamics and information theory measure disorder and uncertainty. In computational thermodynamics, entropy quantifies the number of microstates, while in information theory it represents the amount of information needed to describe a system, highlighting deep connections between physical and informational entropy.

6. In what ways could real-time computational simulations revolutionize the control of industrial processes?
Answer: Real-time simulations enable dynamic monitoring and control of processes, allowing adjustments to optimize efficiency and safety. By predicting system behavior on-the-fly, these simulations can reduce downtime, lower energy consumption, and improve product quality in manufacturing.

7. How might coupling computational thermodynamics with experimental data enhance model accuracy?
Answer: Integrating experimental measurements with simulations allows for calibration and validation of models. This hybrid approach improves the predictive power of computational thermodynamics by reducing uncertainties and refining the parameters used in simulations.

8. What role do phase diagrams play in computational thermodynamics, and how can simulations improve their accuracy?
Answer: Phase diagrams map the equilibrium states of a system as functions of temperature, pressure, and composition. Simulations can predict phase boundaries and critical points with high precision, providing insights into material behavior and guiding the synthesis of new compounds.

9. How can advancements in machine learning accelerate discoveries in computational thermodynamics?
Answer: Machine learning algorithms can analyze large simulation datasets, identify patterns, and optimize parameters automatically. This accelerates the discovery of new materials, improves reaction yield predictions, and enhances our understanding of complex thermodynamic phenomena.

10. What potential does computational thermodynamics have in addressing global energy challenges?
Answer: By modeling energy conversion and storage processes at the molecular level, computational thermodynamics can lead to breakthroughs in battery technology, fuel cells, and renewable energy systems. Optimized thermodynamic cycles can improve efficiency and reduce the environmental impact of energy production.

11. How might quantum computing impact the future of computational thermodynamics?
Answer: Quantum computing could handle the complex calculations of thermodynamic systems much faster than classical computers. This would enable the simulation of larger systems with higher accuracy, opening new avenues for understanding phase transitions and non-equilibrium processes.

12. What are the ethical implications of relying on computational models for critical industrial and environmental decisions?
Answer: As computational models increasingly inform decisions in industry and policy, ensuring their accuracy and transparency becomes crucial. Ethical considerations include the potential for bias, the impact of errors on public safety and the environment, and the need for responsible data management and model validation.

Computational Thermodynamics: Numerical Problems and Solutions

1. Calculate the energy of a photon with a wavelength of 600 nm using E = hc/λ. (h = 6.626×10⁻³⁴ J·s, c = 3.0×10⁸ m/s)
Solution:
λ = 600 nm = 600×10⁻⁹ m
E = (6.626×10⁻³⁴ × 3.0×10⁸) / (600×10⁻⁹)
= (1.9878×10⁻²⁵ J·m) / (600×10⁻⁹ m)
≈ 3.313×10⁻¹⁹ J.

2. For a two-level system with energies 0 and 1 eV at T = 300 K, calculate the partition function Z. (k_B = 8.617×10⁻5 eV/K)
Solution:
Z = e^(–0/ (k_BT)) + e^(–1/(8.617×10⁻5×300))
= 1 + e^(–1/(0.02585))
= 1 + e^(–38.67)
≈ 1 + 1.57×10⁻17 ≈ 1.

3. Determine the probability of the excited state (1 eV) for the system in Problem 2.
Solution:
P_excited = e^(–1/0.02585) / Z
≈ e^(–38.67) / 1
≈ 1.57×10⁻17.

4. Calculate the change in entropy ΔS when a system absorbs 250 J of heat reversibly at 350 K.
Solution:
ΔS = Q/T = 250 J / 350 K ≈ 0.714 J/K.

5. A Carnot engine operates between 500 K and 300 K. Calculate its maximum efficiency.
Solution:
η = 1 – T_c/T_h = 1 – 300/500 = 1 – 0.6 = 0.4 or 40%.

6. For an ideal gas undergoing an isothermal expansion at 400 K from 1.0 L to 3.0 L (1 L = 0.001 m³) for 1 mole, calculate the work done. (R = 8.314 J/(mol·K))
Solution:
W = nRT ln(V_f/V_i)
= 1×8.314×400×ln(3.0/1.0)
= 3325.6×ln(3)
≈ 3325.6×1.0986
≈ 3653 J.

7. A reaction has ΔH = -80 kJ/mol and ΔS = -200 J/(mol·K). Calculate ΔG at 350 K.
Solution:
ΔG = ΔH – TΔS
= (-80,000 J/mol) – 350×(-200 J/mol·K)
= -80,000 + 70,000
= -10,000 J/mol.

8. For a system with a partition function Z = 50 at T = 300 K, calculate the Helmholtz free energy F. (k_B = 1.38×10⁻²³ J/K)
Solution:
F = –k_BT ln(Z)
= –1.38×10⁻²³×300×ln(50)
= –4.14×10⁻²¹×3.912
≈ –1.619×10⁻²⁰ J.

9. In a Monte Carlo simulation, if each iteration takes 5×10⁻⁵ s and 2×10⁶ iterations are required, calculate the total simulation time.
Solution:
Total time = 2×10⁶ × 5×10⁻⁵ s
= 100 s.

10. For a system of 500 particles, if each particle has 3 accessible energy states, determine the total number of microstates.
Solution:
Total microstates = 3^500.

11. Calculate the average energy ⟨E⟩ of a system with two energy levels, 0 and 2 eV, at T = 300 K. (k_BT ≈ 0.02585 eV)
Solution:
Partition function, Z = 1 + e^(–2/0.02585) ≈ 1 + e^(–77.3) ≈ 1.
⟨E⟩ = (0×1 + 2 eV × e^(–77.3))/Z ≈ 0 eV (since e^(–77.3) is negligible).

12. A computational simulation yields ΔS = 2.5 J/(mol·K) for a phase change. If 0.5 mol of a substance undergoes this phase change at constant temperature, calculate the total entropy change.
Solution:
Total ΔS = 0.5 mol × 2.5 J/(mol·K) = 1.25 J/K.