At the heart of quantum mechanics lies a principle that challenges our classical intuitions: Heisenberg’s Uncertainty Principle. This foundational concept asserts that certain pairs of physical properties, such as position and momentum, cannot both be precisely known at the same time. The more accurately we know one, the less precisely we can know the other. This relationship is not a flaw in instrumentation but a fundamental property of nature itself.
The uncertainty principle marks a significant departure from classical physics, forming a cornerstone of modern physics. It has reshaped our understanding of matter, causality, and determinism at microscopic scales. Before students begin to fully appreciate this profound shift, it is crucial to build a solid foundation in atomic physics, including core ideas such as quantum numbers and electron configuration and the structure of the atom.
Heisenberg’s Uncertainty Principle is not a theoretical curiosity; it has practical consequences across many branches of quantum theory. In condensed matter physics, it explains the delocalized behavior of electrons in solids, contributing to the formation of band structures in semiconductors. It is also a guiding principle in nuclear physics, influencing key processes such as nuclear fission, nuclear fusion, and nuclear reactions. Even the understanding of radioactivity and isotopes hinges on the probabilistic nature of quantum decay—a direct implication of uncertainty.
For students studying particle physics, the uncertainty principle is critical to interpreting how bosons and fermions interact via the fundamental forces. The fleeting existence of virtual particles in force mediation is also permitted by temporary violations of energy conservation allowed under the time-energy uncertainty principle. A good overview of these quantum interactions can be found in Scientific American’s guide to quantum reality.
To appreciate the deeper formalism of the uncertainty principle, students should explore quantum field theory, where particles emerge as excitations in quantum fields. The principle also ties into phenomena such as quantum entanglement and quantum superposition, which both defy classical notions of separability and determinism. These concepts are no longer fringe; they form the basis for technologies like quantum computing, which harness quantum uncertainty for unprecedented computational power.
In quantum tunneling, particles pass through potential barriers they would classically be unable to cross—an outcome made possible because their position and energy are not simultaneously well-defined. Such behavior is modeled through the wave function and Schrödinger’s Equation, which offer a statistical interpretation of a particle’s possible states rather than a deterministic trajectory.
Students also gain deeper insight by understanding wave-particle duality. This principle, validated through experiments such as electron diffraction and the double-slit experiment, shows that matter exhibits both wave and particle characteristics depending on how it is measured. The uncertainty principle naturally emerges from this duality and highlights why classical intuitions fail in quantum domains.
Finally, to formalize these probabilistic patterns, students are encouraged to study statistical mechanics, which connects microscopic uncertainty to macroscopic thermodynamic behavior. This helps contextualize the broader implications of Heisenberg’s Uncertainty Principle, revealing how it not only governs atomic systems but also informs models in cosmology, thermodynamics, and quantum information theory.
In sum, understanding Heisenberg’s Uncertainty Principle is not merely a theoretical exercise—it is a gateway to interpreting the quantum fabric of the universe. It compels us to revise long-held assumptions about measurement, determinism, and reality itself.

Table of Contents
Formal Statement of the Principle
\[
\Delta x \cdot \Delta p \geq \frac{\hbar}{2}
\]
\[
\begin{align*}
\text{Where:} \\
\Delta x & = \text{Uncertainty in the position of the particle} \\
\Delta p & = \text{Uncertainty in the momentum of the particle} \\
\hbar & = \frac{h}{2\pi} \approx 1.0545718 \times 10^{-34} \, \text{J} \cdot \text{s} \quad \text{(Reduced Planck’s constant)}
\end{align*}
\]
This inequality expresses a fundamental limitation: the product of the uncertainties in a particle’s position and momentum can never be smaller than ℏ/2. This minimum threshold has far-reaching implications. If a particle’s position is known with high precision (Δx is small), then its momentum must be highly uncertain (Δp is large). Conversely, knowing a particle’s momentum very precisely necessitates a large uncertainty in its position.

This image depicts a mathematical representation of Heisenberg’s Uncertainty Principle, showing how decreasing the uncertainty in a particle’s position (Δx) inevitably increases the uncertainty in its momentum (Δp), and vice versa. The curve follows a hyperbolic shape indicating the lower bound defined by ℏ⁄2. Any values below this curve fall into the shaded red region labeled “Forbidden Region,” symbolizing that such simultaneous precision in position and momentum is not physically attainable. This graph is widely used to visualize the fundamental quantum constraint imposed by the uncertainty principle.
Momentum is defined as the product of mass and velocity, p = mv. Therefore, when discussing uncertainty in momentum, we are actually dealing with three interrelated variables: mass, velocity, and position. For a given uncertainty in position, a larger mass corresponds to a smaller uncertainty in velocity, which aligns with our intuitive sense—heavier objects tend to behave more predictably than lighter ones under the same conditions. This also explains why quantum uncertainty becomes significant primarily for very small particles like electrons.
One might wonder why physicists often express the uncertainty principle in terms of momentum rather than velocity. The reason is both mathematical and conceptual: momentum is a conserved quantity in physics, making it more fundamental in many physical laws and formulations. In quantum mechanics, momentum is the variable that directly appears in wavefunctions and operator equations. Unlike velocity, which depends on the choice of coordinate system and reference frame, momentum has clearer transformation properties under relativity and symmetry operations, making it the preferred quantity in both theoretical and experimental physics.
Digging Deeper: Mathematical Insights and Classical Comparisons
Understanding the Role of Momentum: Mass, Velocity, and Position
In classical mechanics, momentum is defined as:
\( p = mv \)
where \( p \) is momentum, \( m \) is mass, and \( v \) is velocity.
When applying the Heisenberg Uncertainty Principle,
\( \Delta x \cdot \Delta p \geq \frac{\hbar}{2} \)
we see that uncertainty in momentum (Δp) includes contributions from both mass and velocity. For particles with a large mass, even if Δx is small, Δv can be correspondingly smaller—suggesting more “predictable” behavior. This is why macroscopic objects don’t show obvious quantum behavior.
Scientists prefer to work with momentum rather than velocity because momentum is conserved in isolated systems and appears naturally in the mathematical formulations of quantum mechanics. Momentum is the conjugate variable to position in quantum theory, and the momentum operator
\( \hat{p} = -i\hbar \frac{d}{dx} \)
plays a fundamental role in defining a particle’s wavefunction and energy.
Classical vs Quantum Intuitions
| Aspect | Classical View | Quantum View |
|---|---|---|
| Momentum | Product of mass and velocity; well-defined | Operator with probabilistic outcomes; part of wavefunction |
| Velocity | Directly measurable and always known | Uncertain if position is precisely known |
| Measurement | No limit to precision; improves with better tools | Bounded by fundamental quantum uncertainty |
| Object Behavior | Deterministic and continuous | Probabilistic and discrete at small scales |
This table highlights the shift in worldview that quantum mechanics imposes. While classical physics offers a deterministic framework, quantum mechanics forces us to deal with probabilities and limits imposed by the nature of reality itself.
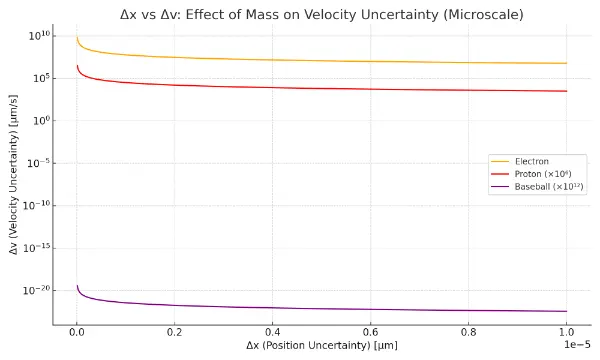
This graph illustrates how mass affects the uncertainty in velocity (Δv) for a given uncertainty in position (Δx), using micrometer-scale units. According to the Heisenberg Uncertainty Principle, Δx and Δp (momentum uncertainty) are inversely related. Since momentum p = mv, the velocity uncertainty Δv = ℏ / (2·m·Δx). The graph shows that:
The electron, being very light, has a large Δv for small Δx.
The proton, with more mass, shows lower Δv under the same Δx.
The baseball, with macroscopic mass, has such low Δv that it appears almost flat—approaching classical predictability.
This illustrates how quantum uncertainty dominates at small mass scales, while classical behavior emerges at larger masses.
This principle reveals a profound truth about the quantum world—it is inherently probabilistic. Unlike classical physics, where quantities like position and velocity can be known exactly and simultaneously, quantum physics introduces a natural boundary to such determinism. This is not due to technological limitations but arises from the mathematical and physical framework of quantum theory itself.
Importantly, this relationship does not imply that a particle does not have position and momentum, but rather that these properties cannot be precisely defined or simultaneously known within the framework of nature. The effect becomes more pronounced as particle mass decreases, which is why it dominates at the atomic and subatomic scale. In macroscopic systems, the value of ℏ is so small that quantum uncertainties are negligible, which is why classical physics works well in everyday life.
To see how this works mathematically, one can derive the uncertainty principle using principles from wave mechanics and operator algebra in quantum theory. In operator form, position and momentum are non-commuting observables, and this non-commutativity leads directly to the uncertainty relation through Robertson’s inequality. Non-commutable observables are pairs of physical quantities in quantum mechanics—like position and momentum—whose measurement order affects the outcome. They cannot be precisely known at the same time due to their operators not commuting (i.e., AB ≠ BA). For further background on this derivation, see Stanford Encyclopedia of Philosophy on Quantum Uncertainty.
The uncertainty principle also provides the rationale behind many modern experimental techniques. For example, in scanning tunneling microscopy (STM), the finite uncertainty in energy allows electrons to tunnel through classically forbidden barriers. In quantum optics and atomic clocks, the principle limits the precision of frequency and time measurements. This is why new technologies often aim to approach—but never violate—this fundamental limit.
As quantum technologies advance, including developments in quantum metrology, engineers and physicists work to reduce uncertainties in one variable (e.g., position) while tolerating increased uncertainty in the conjugate variable (e.g., momentum). This tradeoff is at the heart of squeezed states of light used in gravitational wave detection (e.g., LIGO) and in ultra-precise sensors.

This abstract digital artwork symbolically represents the concept of squeezed states in quantum physics. Radiating concentric waves indicate a squeezed uncertainty ellipse—narrow in one dimension and elongated in the other—visually capturing the tradeoff dictated by Heisenberg’s Uncertainty Principle. The glowing central beam hints at high-precision laser applications in quantum metrology, while the surrounding interference patterns evoke gravitational wave detection as performed by observatories such as LIGO. The color gradient from blue to orange alludes to the shift in uncertainty domains, reflecting how experimental physicists manipulate quantum states to enhance measurement sensitivity in cutting-edge technologies.
Thus, the formal statement of Heisenberg’s Uncertainty Principle is not just a compact inequality—it encapsulates the departure of quantum physics from deterministic classical laws and sets the limits on what can be known about the physical world. It serves as a gateway to understanding the mathematical structure and philosophical implications of quantum mechanics.
Physical Meaning and Interpretation
The principle is not merely a statement about measurement limitations but reveals the fundamental wave-particle duality of matter. In quantum mechanics, particles like electrons and photons exhibit both wave-like and particle-like behavior. The wavefunction (ψ) describes the probability distribution of a particle’s position and momentum.
Position and Momentum Relationship:
A particle described by a sharply peaked wavefunction (well-defined position) must consist of many waves with a wide range of wavelengths (implying uncertain momentum).
Conversely, a wavefunction with a well-defined wavelength (and therefore momentum) is spread out in space, leading to a poorly defined position.
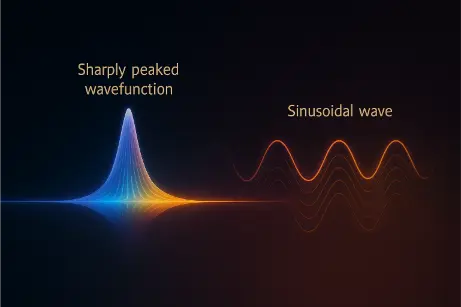
This scientific digital artwork represents the fundamental trade-off between position and momentum uncertainties as described by Heisenberg’s Uncertainty Principle. On the left, a sharply peaked wave packet indicates a precise position, created by overlapping many waves of different wavelengths—signifying high momentum uncertainty. On the right, a single, smooth sinusoidal wave shows clear momentum (via defined wavelength) but is spread across space, reflecting an imprecise position. This duality is central to quantum mechanics and underpins phenomena like diffraction and quantum tunneling.
Inherent Uncertainty:
No matter how advanced our measuring devices become, we cannot bypass this fundamental uncertainty.
Attempting to measure the position of an electron more accurately would disturb its momentum due to the interaction (such as scattering photons off the electron).
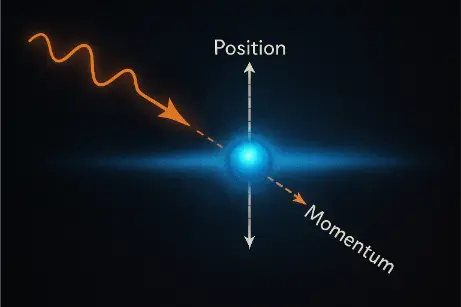
This conceptual artwork illustrates the fundamental limit of measurement in quantum mechanics. A lone electron is shown amidst a dark quantum field, surrounded by directed beams of light representing probing photons. Upon striking the electron, the photons scatter in different directions, visually symbolizing the disturbance in the particle’s momentum. The interaction evokes the principle that increasing the precision of a position measurement inherently disrupts momentum due to quantum interactions. This phenomenon is not a flaw of our instruments but a built-in characteristic of reality governed by Heisenberg’s Uncertainty Principle.
Derivation (Qualitative Overview)
The uncertainty principle can be qualitatively derived from the properties of Fourier transforms, which relate a wave’s spatial distribution to its momentum distribution. This mathematical tool helps translate between the position-space and momentum-space representations of a particle’s state.
In wave mechanics, a particle’s position is described by a wave packet, a combination of many waves with different wavelengths.
A narrow wave packet (precise position) requires a broad range of wavelengths (uncertain momentum).
A broad wave packet (uncertain position) can consist of waves with nearly the same wavelength (precise momentum).
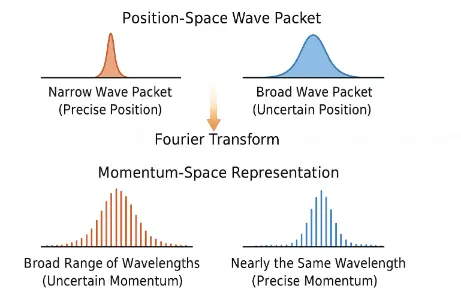
This wave-based description naturally leads to the uncertainty relationship between position and momentum. Fourier analysis shows that a localized function in one domain corresponds to a spread-out function in the conjugate domain. Thus, the uncertainty principle is deeply embedded in the mathematical language of waves and signals—a principle that extends well beyond physics into fields like signal processing, acoustics, and electrical engineering.
The above digital vector illustration offers a profound visual metaphor for the heart of Heisenberg’s uncertainty principle. On the left, a tightly localized wave packet in position space reflects a high degree of spatial precision. Yet, beneath it lies a wide and chaotic distribution of momenta, implying that clarity of position dissolves our grasp on momentum. On the right, the opposite unfolds: a smooth, extended wave packet signifying positional ambiguity but paired with a sharply focused frequency distribution, denoting momentum precision. This symmetry—made visible through the Fourier transform—mirrors the universe’s quiet refusal to grant total knowledge. It is not a flaw in our methods, but a whisper from nature itself: to know fully is to disturb balance.
Implications of the Uncertainty Principle
Measurement Limits
The uncertainty principle imposes a fundamental limit on how precisely we can measure quantum systems. It reveals that certain pairs of physical properties, known as complementary variables (like position and momentum, or energy and time), cannot both be known to arbitrary precision. This is not a flaw in our instruments, but a profound truth about the structure of nature. Even the most ideal measuring device cannot simultaneously determine these properties beyond the limit set by ℏ/2.
Quantum Behavior vs. Classical Intuition
In classical mechanics, it is assumed that both position and momentum can be measured exactly at any instant. The uncertainty principle breaks this classical assumption, highlighting the stark difference between classical and quantum physics. For microscopic particles, this uncertainty significantly influences behavior, such as electron clouds in atoms or the spread of a photon beam. In contrast, for macroscopic objects like tennis balls or planets, the uncertainty is negligible due to their much larger mass.
Zero-Point Energy
Particles confined in a finite space, such as electrons in atoms, cannot have zero kinetic energy because that would require both position and momentum to be precisely known. This explains why electrons do not collapse into the nucleus and why atoms have zero-point energy—the lowest possible energy a quantum system can have. This concept plays a crucial role in understanding atomic stability, molecular vibrations, and phenomena like the Casimir effect.
The uncertainty in energy and position allows particles to “tunnel” through potential energy barriers that they classically shouldn’t be able to cross. This phenomenon is essential in many natural and technological processes. It explains how nuclear fusion occurs in stars, even when particles lack the classical energy needed to overcome electrostatic repulsion. It also underpins the operation of tunnel diodes and quantum dots, and has become foundational to the rapidly growing field of quantum electronics. Watch the Quantum Tunneling video.
Stability of Matter
Without the uncertainty principle, electrons would spiral into the nucleus, making atoms unstable. The principle ensures that confining an electron too tightly increases its momentum (and kinetic energy), which acts against collapse. This mechanism prevents matter from degenerating under its own electromagnetic forces, and provides the foundation for the structure of all matter, from simple hydrogen atoms to complex molecules and crystalline solids.
Extensions to Other Conjugate Variables
- Energy-Time Uncertainty Relation:
\[
\Delta E \cdot \Delta t \geq \frac{\hbar}{2}
\]
This relation implies that the energy of a system can fluctuate if the observation time is very short. These fluctuations are not artifacts of measurement but reflect real transient processes, enabling the temporary appearance of virtual particles in quantum field theory. These effects underpin many modern theories of particle interactions and vacuum fluctuations. See this Scientific American article on virtual particles for a clear overview. - Angular Position and Angular Momentum:
\[
\Delta \theta \cdot \Delta L \geq \frac{\hbar}{2}
\]
In rotational systems, if a particle’s angular position (θ) is known with great precision, its angular momentum (L) becomes uncertain. This is important in systems like ring-shaped molecules, superconducting loops, and rotating quantum fluids. The quantization of angular momentum also arises from this conjugate relationship, governing the behavior of atomic orbitals and the fine structure of energy levels.
Experimental Evidence
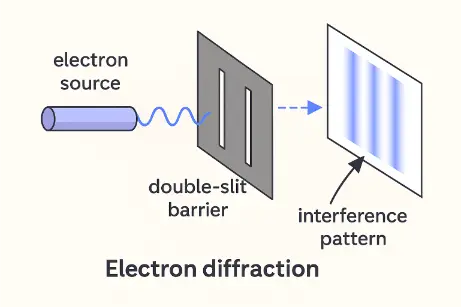
- Electron Diffraction:
When electrons pass through a narrow slit, their wave-like nature causes diffraction patterns. Narrowing the slit (reducing Δx) increases the spread of the diffraction pattern (increasing Δp). This is direct visual evidence of the uncertainty principle at work. It was first demonstrated in the 1927 Davisson–Germer experiment and continues to be a foundational result in quantum mechanics.
- Scanning Tunneling Microscope (STM):
The operation of the STM relies on quantum tunneling, a direct consequence of the uncertainty in energy and position. This enables imaging of individual atoms on a surface with unprecedented resolution.

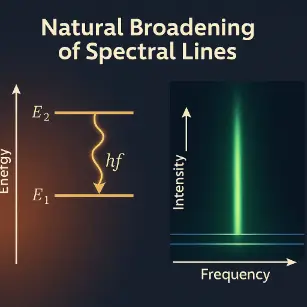
- Spectral Line Broadening:
The energy-time uncertainty relation explains the natural broadening of spectral lines in atomic emissions. Excited atomic states that decay quickly have less well-defined energies, leading to broader spectral lines. This phenomenon is crucial for interpreting spectroscopic data in fields ranging from astrophysics to laser physics.
Applications of Heisenberg’s Uncertainty Principle in Modern Society
High-Resolution Imaging and Electron Microscopy
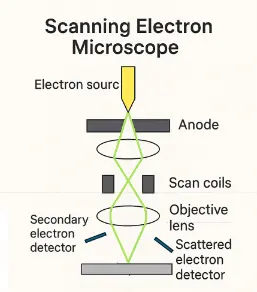
This simplified scientific illustration displays the essential working components of a Scanning Electron Microscope (SEM). The diagram includes the electron source at the top, which emits a focused beam accelerated past the anode. The beam is condensed by magnetic condenser lenses and directed by scan coils across the sample surface via the objective lens. Interactions between the electron beam and the sample produce various signals: secondary electrons, emitted from near the surface, are captured by the secondary electron detector to form high-resolution topographic images; backscattered (elastically scattered) electrons, indicative of atomic number contrast, are detected by the scattered electron detector. The interplay of precision electron control and probabilistic quantum interactions governed by the Heisenberg Uncertainty Principle makes SEM a cornerstone technology in nanoscience and materials research.
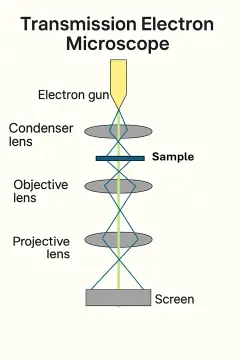
This simplified 2D digital diagram presents the basic structure of a Transmission Electron Microscope (TEM), a powerful instrument used to study the internal structure of materials at the atomic level. At the top, the electron gun emits a focused beam of electrons that is condensed by the condenser lens and directed onto a thin sample. Electrons that pass through the sample carry information about its internal composition. These transmitted electrons are then refined by the objective lens to form an initial image and further magnified by the projector lens, ultimately forming a detailed projection on the viewing screen. Unlike scanning electron microscopes, which gather surface details, TEM provides insight into the inner morphology of nanoscale structures. The clarity and resolution of the image are limited by quantum effects, including those described by the Heisenberg Uncertainty Principle, which constrains how precisely one can simultaneously know the electron’s position and momentum during high-energy imaging.

This image displays three sophisticated electron microscopes placed side-by-side in a research laboratory: a Scanning Electron Microscope (SEM) with its characteristic cylindrical column and multiple detectors; a Transmission Electron Microscope (TEM) with a tall vertical vacuum column for imaging ultra-thin samples; and an Environmental Scanning Electron Microscope (ESEM), equipped to analyze specimens in low vacuum or humid environments without prior coating. These devices are critical in modern science for resolving features at the atomic and molecular scale, enabling research in fields such as materials science, biomedical engineering, and quantum nanostructures.
Quantum Computing and Cryptography

This digital illustration visualizes the inner workings of a quantum computer, featuring glowing qubits suspended in superposition and entangled via energy threads, symbolizing non-classical correlations. The ethereal blue and grid-like background evokes a futuristic data environment, highlighting the contrast between classical binary logic and the probabilistic, multidimensional logic of quantum information. Inspired by the Heisenberg Uncertainty Principle, this depiction reflects how quantum systems exploit uncertainty as a computational asset, allowing simultaneous exploration of numerous states. The image serves to bridge abstract quantum theory with real-world innovation in quantum engineering and information science.

This digital illustration captures the essence of quantum cryptography. At the center, a glowing entangled particle is connected to three luminous quantum keys, representing the distribution of encryption keys. A bright padlock symbolizes secure communication, while the background features cascading binary code to reflect the digital context. The image emphasizes how Heisenberg’s Uncertainty Principle is harnessed in quantum key distribution to ensure message integrity and prevent undetected interception.
Semiconductor Physics and Miniaturization Limits
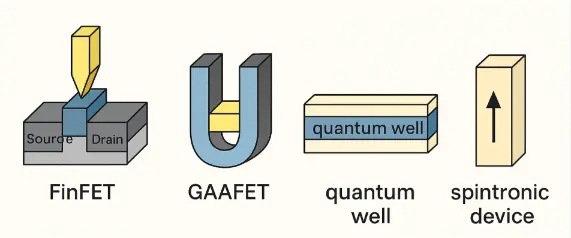
This digital illustration presents four cutting-edge semiconductor device architectures that exemplify the fusion of quantum mechanics and engineering innovation. FinFETs (Fin Field-Effect Transistors) and GAAFETs (Gate-All-Around FETs) represent the evolution of traditional transistors into 3D architectures, allowing better electrostatic control and reduced leakage. Quantum wells confine charge carriers within ultra-thin layers, enabling quantum tunneling and enhanced mobility. Spintronic devices exploit electron spin in addition to charge, opening new frontiers in logic and memory. These structures symbolize a shift in electronics where quantum uncertainty is not just tolerated but embraced as a design principle, turning probabilistic phenomena into computational advantage.
Emerging and Future Technologies

Quantum Metrology Devices – Atomic Clock, Gravimeter, and Interferometer
Description: This digital illustration showcases three advanced tools used in quantum metrology: an atomic clock for ultra-precise timekeeping, a gravimeter for detecting tiny variations in gravitational fields, and an interferometer for measuring minuscule distances or wave interference. These devices leverage the principles of the Heisenberg Uncertainty Principle, optimizing measurement accuracy by balancing trade-offs between precision and disturbance in quantum systems. The sleek, glowing depiction emphasizes their role in pushing the frontiers of detectability in physics and engineering.

This digital illustration artistically captures the function of the Laser Interferometer Gravitational-Wave Observatory (LIGO), which measures cosmic ripples in spacetime using long interferometric arms and finely tuned mirrors. The beams of coherent laser light split and travel down orthogonal arms, where even the slightest perturbation caused by a passing gravitational wave alters the interference pattern upon recombination. LIGO’s extreme sensitivity is made possible by quantum optics and techniques such as squeezed light states, which reduce measurement noise dictated by the Heisenberg Uncertainty Principle. In this illustration, visual cues such as tremors in the laser paths and stylized wavefronts convey how the observatory listens not just to the universe’s cataclysms but also to the delicate whispers of quantum indeterminacy.

This digital illustration explores the speculative yet increasingly intriguing field of quantum biology, where the Heisenberg Uncertainty Principle is hypothesized to influence biological processes. A bird in mid-flight symbolizes magnetoreception guided by quantum entanglement, while molecular structures represent enzymatic reactions that may leverage quantum tunneling. Glowing quantum paths and wave-like overlays suggest the presence of uncertainty at the core of life’s decision-making processes. The image bridges quantum physics and the life sciences, visually posing the provocative question: Could evolution itself have harnessed quantum indeterminacy?
Conclusion on The Application of Heisenberg Uncertainty Principle on Modern Society
Why Study Heisenberg’s Uncertainty Principle
Limits of Measurement in Quantum Systems
Mathematical Expression and Physical Interpretation
Impacts on Experimental Physics
Conceptual Foundations and Misconceptions
Relevance to Quantum Information and Cryptography
Influence on Emerging Technologies
Gateway to Philosophical and Scientific Inquiry
Preparation for Advanced Study and Research
Frequently Asked Questions About Heisenberg’s Uncertainty Principle
1. What exactly is the Heisenberg Uncertainty Principle (HUP)?
Heisenberg’s Uncertainty Principle is a cornerstone of quantum mechanics, formulated by Werner Heisenberg in 1927. It asserts that there are fundamental limits to how precisely we can simultaneously know certain pairs of physical properties of a quantum system. The most well-known example is the position and momentum of a particle: the more precisely we determine the particle’s position, the less precisely we can know its momentum, and vice versa. This is not a statement about the limitations of our measuring instruments, but a reflection of the inherent probabilistic nature of reality at quantum scales. The uncertainty is quantitatively expressed as Δx × Δp ≥ ℏ/2, where Δx is the uncertainty in position, Δp is the uncertainty in momentum, and ℏ is the reduced Planck constant. This principle challenges classical intuitions and forms the bedrock of quantum theory, influencing everything from particle behavior to the structure of atoms and the limits of measurement precision.
2. Is the uncertainty due to our lack of knowledge or something deeper?
This is a fundamental and often misunderstood aspect of quantum theory. In classical physics, uncertainty typically arises from incomplete knowledge or limitations in measurement tools. However, in quantum mechanics, the uncertainty described by Heisenberg is not due to ignorance or instrument flaws; it is an intrinsic feature of nature. Even in a theoretically perfect experiment, a particle simply does not possess exact values for certain property pairs simultaneously. This is due to the wave-like nature of quantum particles, where properties like position and momentum are described by a probability distribution rather than fixed quantities. The uncertainty principle reflects a limit to the determinacy of physical states, suggesting that reality at the quantum level is not deterministic but governed by probabilities. This philosophical shift from certainty to indeterminacy has profound implications, influencing debates about the nature of reality, causality, and the limits of human knowledge.
3. Does the uncertainty principle only apply to position and momentum?
Not at all. While position and momentum are the most commonly cited pair of conjugate variables governed by the uncertainty principle, many other pairs are similarly constrained. The principle applies to any pair of non-commuting observables—quantities whose operators do not commute in the mathematical framework of quantum mechanics. For example, energy and time form another such pair: the more precisely the energy of a system is known, the less precisely we can determine the duration over which that energy is defined. This is crucial in understanding phenomena such as the natural linewidth in atomic emissions and the lifetime of unstable particles. Other examples include angular position and angular momentum, electric and magnetic field strengths in quantum electrodynamics, and number-phase pairs in quantum optics. These generalized uncertainty relationships expand the reach of Heisenberg’s insight to a broad range of physical systems, from atoms and molecules to quantum fields and cosmological models.
4. How does HUP affect quantum computing?
Heisenberg’s Uncertainty Principle plays a foundational role in the operation of quantum computers. Unlike classical bits, which are binary and exist strictly as 0 or 1, quantum bits (qubits) can exist in superpositions—linear combinations of both 0 and 1 states. This superposition is enabled by the probabilistic nature of quantum systems, rooted in HUP. Because of this, quantum computers can process many possibilities at once, exploring vast computational spaces in parallel. This allows them to tackle certain problems, like prime factorization (as in Shor’s algorithm), exponentially faster than classical counterparts. Moreover, HUP also informs the design of quantum gates and the control of qubit coherence. The very act of manipulating or measuring a qubit involves uncertainty, which must be managed carefully to avoid decoherence and loss of information. Quantum error correction techniques are, in part, designed to mitigate the practical consequences of these uncertainties. Ultimately, quantum computing is not merely built in spite of HUP—it is built because of it.
5. Can we overcome the limitations set by HUP?
We cannot eliminate the uncertainty principle, but we can manipulate and work within its constraints. One technique is quantum squeezing, which involves reducing the uncertainty in one variable of a conjugate pair at the expense of increasing it in the other. This approach is widely used in quantum optics and precision measurement devices like gravitational wave detectors. In metrology, squeezed states of light allow measurements that surpass the standard quantum limit, pushing the sensitivity of devices like interferometers to new heights. Another way to cope with HUP is by averaging over many measurements, which can reduce statistical noise but does not bypass the fundamental limits. In quantum information theory, clever use of entanglement and correlation enables indirect inferences about conjugate variables with high precision. Thus, while the uncertainty principle sets an unbreachable boundary, it also inspires new ways to encode, measure, and exploit quantum information by reshaping our understanding of what is possible.
6. How does HUP impact electron microscopes?
Electron microscopes rely on the wave-like behavior of electrons to achieve resolutions far beyond those possible with visible light. The shorter de Broglie wavelength of electrons allows imaging at atomic scales, but this comes with a quantum trade-off. Narrowing the beam to focus on a small region (decreasing position uncertainty, Δx) increases momentum uncertainty (Δp), causing the electrons to spread and reducing image sharpness. This balance must be carefully managed in Scanning Electron Microscopes (SEM) and Transmission Electron Microscopes (TEM), where beam convergence and detector placement are engineered to optimize resolution and signal clarity. In advanced techniques like cryo-electron microscopy, these principles are taken to the limit to reconstruct molecular structures with near-atomic precision. HUP also affects how secondary and backscattered electrons are interpreted, influencing contrast and noise in imaging. In essence, the design and operation of high-resolution electron microscopes are not merely constrained by HUP—they are guided by it, transforming a quantum limit into a lens of discovery.
7. Is HUP involved in quantum cryptography?
Yes, HUP is central to the security guarantees of quantum cryptography. In protocols like BB84, quantum key distribution (QKD) relies on the principle that any attempt to measure or intercept a quantum state will unavoidably disturb it. This is a direct consequence of HUP: the act of measurement changes the system in a detectable way. If an eavesdropper tries to intercept quantum keys encoded in photon polarization states, their intrusion introduces errors that can be spotted by the communicating parties. This makes the very process of spying self-defeating, as it reveals the spy’s presence. Unlike classical cryptography, which depends on computational complexity (and can potentially be broken with powerful enough computers), quantum cryptography derives its strength from the laws of physics themselves. Countries and research institutions are developing quantum-secure networks based on these principles, ushering in a future where digital security is no longer merely a matter of algorithms but of unbreakable physical law.
8. Is there experimental proof of HUP?
Heisenberg’s Uncertainty Principle is supported by a vast body of experimental evidence across diverse quantum systems. The famous double-slit experiment with single electrons or photons shows interference patterns that arise precisely because particles do not have well-defined paths—consistent with uncertainty in position and momentum. Experiments in quantum optics, such as homodyne detection and photon counting, have measured uncertainties in conjugate variables like phase and amplitude. Atomic spectroscopy reveals the natural linewidth of emission lines due to energy-time uncertainty, and precision measurements in quantum tunneling confirm the probabilistic nature of particle penetration through barriers. These and countless other tests have confirmed that HUP is not just a theoretical curiosity but a measurable and predictable aspect of quantum reality. Indeed, no experiment to date has ever contradicted the uncertainty principle, making it one of the most robust and validated foundations in all of physics.
9. How does HUP relate to quantum tunneling?
Quantum tunneling is one of the most direct and dramatic consequences of the uncertainty principle. In classical physics, a particle cannot pass through a barrier if it lacks sufficient energy. But in the quantum realm, the wavefunction of a particle has a finite probability of extending through and beyond the barrier, enabling the particle to appear on the other side. This is because the particle’s energy and position are not strictly defined, and the uncertainty allows for transient violations of classical energy constraints. Quantum tunneling underlies numerous phenomena, from alpha decay in nuclear physics to the operation of tunnel diodes and the fusion reactions that power the sun. In modern electronics, tunneling imposes design limits on how small and energy-efficient transistors can be. Engineers and physicists alike must consider these quantum effects when working with nanoscale devices. Thus, HUP does not merely describe tunneling—it enables it.
10. Can HUP be visualized or intuitively grasped?
Though abstract, the uncertainty principle can be visualized using several analogies and graphical tools. One common visualization is the wave packet: a quantum particle is represented as a spread-out wave, and the more localized the wave is in space (position), the more it spreads in frequency or wavenumber (momentum). Another helpful metaphor is the phase space ellipse, where the area of the ellipse represents the minimum uncertainty area set by ℏ. Attempts to narrow the ellipse in one direction cause it to expand in the other. A more imaginative analogy is that of a dartboard in a fog: the more precisely you know where a dart lands (sharp position), the more unpredictable its flight path must have been (momentum). While no classical picture can fully capture quantum reality, these visual tools provide insight into the constraints and possibilities introduced by HUP. Ultimately, it invites us to accept a world where knowing everything with certainty is not just hard—it is impossible, and beautifully so.
Conclusion on Heisenberg Uncertainty Principle
Heisenberg Uncertainty Principle: Review Questions
1. What is Heisenberg’s Uncertainty Principle?
Answer: Heisenberg’s Uncertainty Principle states that it is impossible to simultaneously measure the exact position and momentum of a particle. The more precisely one quantity is known, the less precisely the other can be determined.
2. How is the uncertainty principle mathematically expressed?
Answer: It is expressed as Δx·Δp ≥ ħ/2, where Δx is the uncertainty in position, Δp is the uncertainty in momentum, and ħ is the reduced Planck’s constant.
3. Why does the uncertainty principle imply that quantum measurements are probabilistic?
Answer: Because the principle limits the precision with which certain pairs of properties can be known simultaneously, measurements yield a range of probable values rather than exact ones, reflecting the intrinsic probabilistic nature of quantum systems.
4. How does the uncertainty principle affect our understanding of particle behavior at the quantum level?
Answer: It reveals that particles do not have definite positions and momenta until measured, suggesting that particles exist in a superposition of states and that observation fundamentally influences the system.
5. What role does the reduced Planck’s constant (ħ) play in the uncertainty principle?
Answer: The reduced Planck’s constant sets the scale of quantum effects. Its small value means that uncertainty effects are negligible for macroscopic objects but become significant at atomic and subatomic scales.
6. How can the uncertainty principle be demonstrated experimentally?
Answer: Experiments like electron diffraction and the double-slit experiment show interference patterns that arise because particles have inherent uncertainties in their position and momentum, confirming the principle’s predictions.
7. What is the physical significance of the product Δx·Δp being greater than or equal to ħ/2?
Answer: This inequality indicates a fundamental limit to measurement precision, emphasizing that at quantum scales, there is a minimum unavoidable disturbance when measuring complementary properties.
8. How does the uncertainty principle relate to the concept of wave-particle duality?
Answer: The principle is a consequence of the wave-like nature of particles. A particle described by a wavefunction inherently exhibits a spread in position and momentum, leading to the observed uncertainty.
9. In what way does the uncertainty principle challenge classical determinism?
Answer: Unlike classical physics, where properties can be measured exactly, the uncertainty principle implies that at the quantum level, events are inherently probabilistic, challenging the deterministic view of the universe.
10. What are some practical implications of the uncertainty principle in modern technology?
Answer: The uncertainty principle underpins technologies such as electron microscopy and quantum computing. It also influences semiconductor behavior and has led to the development of quantum encryption techniques for secure communication.
Heisenberg Uncertainty Principle: Thought-Provoking Questions
1. How might the uncertainty principle influence our understanding of reality at a fundamental level?
Answer: The uncertainty principle suggests that reality is inherently probabilistic rather than deterministic, challenging our classical intuition. This raises profound philosophical questions about the nature of existence, measurement, and whether particles have properties independent of observation.
2. What implications does the uncertainty principle have for the concept of causality in quantum mechanics?
Answer: Since precise measurement of certain pairs of variables is impossible, the traditional cause-and-effect relationship becomes blurred at quantum scales. This uncertainty forces us to reconsider how events are linked and whether causality is a fixed concept in the quantum realm.
3. How can the uncertainty principle be reconciled with the apparent determinism of macroscopic phenomena?
Answer: Although uncertainty is significant at quantum scales, its effects average out in large systems, leading to predictable, deterministic behavior. This transition from quantum indeterminacy to classical determinism is a key aspect of quantum decoherence and emergent phenomena.
4. In what ways might advancements in measurement technology challenge or confirm the limits set by the uncertainty principle?
Answer: Future technology may allow for more precise measurements that approach the uncertainty limit, further confirming its validity. However, any attempt to surpass these limits will likely reveal new quantum phenomena, reinforcing the principle as a fundamental law of nature.
5. How does the uncertainty principle affect the concept of particle trajectories in quantum mechanics?
Answer: Unlike in classical mechanics, particles in quantum mechanics do not have well-defined trajectories. The uncertainty principle implies that the concept of a precise path becomes meaningless, replaced by probability distributions that describe likely positions and momenta.
6. Could the uncertainty principle have practical applications in emerging quantum technologies?
Answer: Yes, it is fundamental to quantum cryptography, where uncertainty ensures the security of communication. Additionally, quantum computing and sensing devices exploit uncertainty to perform tasks that surpass classical limits in speed and precision.
7. How might the uncertainty principle contribute to our understanding of quantum tunneling phenomena?
Answer: Quantum tunneling, where particles cross energy barriers they classically shouldn’t, relies on the uncertainty in energy and position. Understanding this principle helps explain tunneling in nuclear fusion and semiconductor devices, influencing the design of advanced electronic components.
8. What does the uncertainty principle suggest about the nature of space and time at quantum scales?
Answer: The principle implies that at very small scales, space and time might be quantized, with inherent limits to how precisely they can be measured. This idea supports theories of quantum gravity and may lead to a deeper understanding of the fabric of the universe.
9. How might philosophical interpretations of quantum mechanics be influenced by the uncertainty principle?
Answer: Different interpretations, such as the Copenhagen interpretation or many-worlds theory, address the uncertainty principle in various ways. It challenges the notion of objective reality and prompts debates on whether quantum states represent actual physical properties or just probabilities.
10. In what way does the uncertainty principle affect our understanding of energy fluctuations in the vacuum?
Answer: The uncertainty principle allows for temporary energy fluctuations in the vacuum, leading to the creation of virtual particle-antiparticle pairs. These fluctuations are essential to understanding phenomena like the Casimir effect and the stability of the quantum vacuum.
11. How do the limitations imposed by the uncertainty principle impact experimental designs in quantum mechanics?
Answer: Experimental setups must account for the intrinsic uncertainties when measuring quantum systems. This affects the design of high-precision instruments, the interpretation of data, and the strategies used to isolate quantum effects from noise.
12. What are the potential future research directions that could deepen our understanding of the uncertainty principle?
Answer: Future research may explore the limits of measurement in extreme conditions, the relationship between uncertainty and quantum entanglement, and its implications in quantum gravity. Advancements in technology and theoretical models could lead to new insights into the fundamental structure of reality.
Heisenberg Uncertainty Principle: Numerical Problems
1. Calculate the energy of a photon with a wavelength of 600 nm using E = hc/λ. (h = 4.1357×10⁻¹⁵ eV·s, c = 3.0×10⁸ m/s)
Solution:
λ = 600 nm = 600×10⁻⁹ m
E = (4.1357×10⁻¹⁵ × 3.0×10⁸) / (600×10⁻⁹)
= (1.2407×10⁻⁶) / (600×10⁻⁹)
≈ 2.0678 eV.
2. Determine the ground state energy of an electron in a one-dimensional infinite potential well of width L = 1.0 nm using E₁ = (h²)/(8mL²). (m = 9.11×10⁻³¹ kg, h = 6.626×10⁻³⁴ J·s)
Solution:
L = 1.0×10⁻9 m
E₁ = (6.626×10⁻³⁴)² / (8 × 9.11×10⁻³¹ × (1.0×10⁻9)²)
= 4.39×10⁻67 / (7.288×10⁻48)
≈ 6.02×10⁻20 J
Converting to eV: 6.02×10⁻20 J / 1.602×10⁻19 J/eV ≈ 0.376 eV.
3. Compute the de Broglie wavelength of an electron with kinetic energy 50 eV. (Use E = p²/(2m) and λ = h/p)
Solution:
E = 50 eV = 50 × 1.602×10⁻19 J = 8.01×10⁻18 J
p = √(2mE) = √(2 × 9.11×10⁻31 kg × 8.01×10⁻18 J)
≈ √(1.459×10⁻47) ≈ 1.208×10⁻23 kg·m/s
λ = h/p = 6.626×10⁻34 J·s / 1.208×10⁻23
≈ 5.48×10⁻11 m.
4. Using the uncertainty principle ΔxΔp ≥ h/4π, find the minimum momentum uncertainty Δp if Δx = 1.0×10⁻10 m. (h = 6.626×10⁻34 J·s)
Solution:
Δp ≥ h/(4πΔx) = 6.626×10⁻34 / (4π × 1.0×10⁻10)
≈ 6.626×10⁻34 / (1.2566×10⁻9)
≈ 5.27×10⁻25 kg·m/s.
5. Calculate the de Broglie wavelength of an electron moving at 2.0×10⁶ m/s. (m = 9.11×10⁻31 kg, h = 6.626×10⁻34 J·s)
Solution:
p = m×v = 9.11×10⁻31 × 2.0×10⁶ = 1.822×10⁻24 kg·m/s
λ = h/p = 6.626×10⁻34 / 1.822×10⁻24
≈ 3.637×10⁻10 m.
6. For a hydrogen atom, use the Bohr model to calculate the energy difference (ΔE) between the n=2 and n=1 levels. (E_n = -13.6 eV/n²)
Solution:
E₁ = -13.6 eV, E₂ = -13.6/4 = -3.4 eV
ΔE = E₁ – E₂ = (-13.6) – (-3.4) = -10.2 eV
The energy released is 10.2 eV.
7. Calculate the frequency of a photon with energy 3.0 eV using E = hν. (h = 4.1357×10⁻15 eV·s)
Solution:
ν = E/h = 3.0 eV / 4.1357×10⁻15 eV·s
≈ 7.25×10¹⁴ Hz.
8. An electron in a hydrogen atom is in an energy state of -1.51 eV (n=3). What is the wavelength of the photon emitted when it transitions to n=2 (E = -3.4 eV)? (ΔE = 1.89 eV, use E = hc/λ with hc = 1240 eV·nm)
Solution:
λ = hc/ΔE = 1240 eV·nm / 1.89 eV ≈ 656 nm.
9. A quantum system has an energy uncertainty ΔE = 0.1 eV. Estimate the minimum lifetime Δt using Δt ≈ ħ/ΔE. (ħ = 6.582×10⁻16 eV·s)
Solution:
Δt = 6.582×10⁻16 / 0.1 = 6.582×10⁻15 s.
10. If a photon’s wavelength is measured to be 400 nm, what is its momentum? (p = h/λ, h = 6.626×10⁻34 J·s)
Solution:
λ = 400 nm = 400×10⁻9 m
p = 6.626×10⁻34 / (400×10⁻9) ≈ 1.6565×10⁻27 kg·m/s.
11. Determine the kinetic energy (in eV) of an electron with a momentum of 1.0×10⁻24 kg·m/s. (Use E = p²/(2m), m = 9.11×10⁻31 kg)
Solution:
E = (1.0×10⁻24)² / (2 × 9.11×10⁻31)
= 1.0×10⁻48 / 1.822×10⁻30 ≈ 5.49×10⁻19 J
Converting to eV: 5.49×10⁻19 / 1.602×10⁻19 ≈ 3.42 eV.
12. A quantum system is confined to a region of size 1.0×10⁻9 m. Estimate the minimum energy uncertainty ΔE using ΔE ≈ ħc/Δx, with ħc ≈ 197 eV·nm.
Solution:
Δx = 1.0×10⁻9 m = 1.0 nm
ΔE ≈ 197 eV·nm / 1.0 nm = 197 eV.
