Concept of Quantum Superposition

In classical physics, objects exist in well-defined states. For example, a ball is either on the ground or in the air; it cannot be both simultaneously. However, in quantum mechanics, particles like electrons, photons, and atoms can occupy multiple states simultaneously. This phenomenon is called superposition.

• Mathematically, a quantum system is described by a wavefunction (ψ), which encapsulates all possible states the system can be in. If a quantum particle can exist in two distinct states, say ∣A⟩ and ∣B⟩, the superposition principle states that the system can be in a linear combination of these states:

  ∣Ψ⟩ = α∣A⟩ + β∣B⟩

  Where:

  ∣Ψ⟩ is the superposed state.
  α and β are complex probability amplitudes that determine the likelihood of the system being found in state ∣A⟩ or ∣B⟩ when measured.

  The probabilities of the system being in state ∣A⟩ or ∣B⟩ are given by ∣α∣² and ∣β∣², respectively, with the condition that ∣α∣² + ∣β∣² = 1.

Until a measurement is made, the system exists in both states simultaneously, with certain probabilities for each outcome. Upon measurement, the system “collapses” into one of these possible states.

Examples of Quantum Superposition

Electron Energy States in Atoms

Electrons in atoms are not restricted to a single energy state before measurement. Instead, they can exist in a superposition of energy levels. For example, an electron in a hydrogen atom can be in a superposition of the first and second energy levels. Only when the electron is measured does it “choose” an energy level.

Photon Polarization

Photons (particles of light) can exhibit superposition in their polarization states. A photon can be horizontally polarized (∣H⟩) or vertically polarized (∣V⟩), or it can exist in a superposition of both:

∣Ψ⟩ = (1/2)(∣H⟩ + ∣V⟩)

This principle is exploited in quantum optics and quantum communication systems.

$$|\Psi\rangle = \frac{1}{\sqrt{2}}(|H\rangle + |V\rangle)$$

This principle is exploited in quantum optics and quantum communication systems.

Quantum Bits (Qubits)

In quantum computing, a qubit (quantum bit) can exist in a superposition of both the ∣0⟩ and ∣1⟩ states simultaneously:

$$\mathrm{\mid }\mathrm{\Psi }⟩=\alpha \mathrm{\mid }0⟩+\beta \mathrm{\mid }1⟩$$

This is fundamentally different from classical bits, which can only be 0 or 1 at any given time. Superposition allows quantum computers to process vast amounts of information in parallel, making them exponentially more powerful for certain types of calculations.

Schrödinger’s Cat Thought Experiment

To illustrate the strange implications of quantum superposition on a macroscopic scale, Erwin Schrödinger proposed his famous thought experiment in 1935.

Scenario:

• A cat is placed in a sealed box with a radioactive atom, a Geiger counter, a vial of poison, and a hammer.
• If the atom decays (a quantum event), the Geiger counter triggers the hammer to break the vial, releasing poison and killing the cat.
• If the atom does not decay, the cat remains alive.
• The decay of the atom is a quantum event and is governed by superposition, meaning the atom is both decayed and undecayed until observed.

Implication:
According to the principle of superposition, the cat is simultaneously alive and dead until someone opens the box and observes the system. This paradox highlights the conflict between quantum mechanics and classical intuition, raising profound questions about when and how quantum superpositions “collapse” into definite outcomes.

Mathematical Framework of Superposition

The mathematics of superposition arises from the linearity of the Schrödinger equation, the fundamental equation of quantum mechanics:

$$i\mathrm{\hslash }\frac{\mathrm{\partial }}{\mathrm{\partial }t}\mathrm{\mid }\mathrm{\Psi }(t)⟩=\widehat{H}\mathrm{\mid }\mathrm{\Psi }(t)⟩$$

Where:

∣Ψ(t)⟩ is the system’s wavefunction evolving over time.

Ĥ is the Hamiltonian operator, representing the total energy of the system.

ℏ is the reduced Planck’s constant.

Because the Schrödinger equation is linear, if ∣ψ₁⟩ and ∣ψ₂⟩ are solutions, any linear combination α∣ψ₁⟩ + β∣ψ₂⟩ is also a solution. This property directly leads to the superposition principle.

Measurement and Wavefunction Collapse

A critical feature of superposition is the concept of wavefunction collapse. While a quantum system can exist in multiple states simultaneously, the act of measurement forces the system to randomly “choose” one of these states.

• Before Measurement: The system is in a superposed state.
• Upon Measurement: The system collapses into one of the possible eigenstates with a probability determined by the amplitude squared |α|²
  $\mathrm{}$

This process is inherently probabilistic, and no underlying mechanism in standard quantum mechanics explains how or why the collapse occurs—a major subject of debate in quantum foundations.

This educational illustration portrays the process of wavefunction collapse in quantum mechanics. A particle is initially depicted in a superposition of multiple possible states, visualized through overlapping waveforms or probabilistic layers. Upon measurement, this superposition collapses into a single, well-defined outcome—an eigenstate—determined by the probability amplitude squared. The image captures the dramatic reduction of quantum uncertainty through observation, highlighting the inherently probabilistic nature of quantum measurements. This collapse is central to understanding how quantum systems transition from ambiguity to certainty during interaction with a measuring device, a phenomenon that continues to puzzle and inspire physicists.

Physical and Philosophical Implications

Challenge to Classical Reality

Superposition suggests that particles do not have definite properties until they are observed, undermining the classical notion that objects possess well-defined states independent of measurement.

Quantum Nonlocality

Superposition, when combined with entanglement, leads to the phenomenon of nonlocality, where the measurement of one particle can instantaneously affect another, regardless of distance.

Observer Effect

The fact that observation collapses the wavefunction raises questions about the role of the observer in defining reality. This leads to interpretations like the Copenhagen interpretation and the Many-Worlds interpretation.

Applications of Quantum Superposition

Quantum Computing

Superposition allows quantum computers to perform parallel computations. A qubit in superposition can represent both 0 and 1 simultaneously, enabling quantum algorithms like Shor’s algorithm for factoring and Grover’s algorithm for search.

This digital illustration captures the essence of quantum computing powered by superposition. The image depicts glowing qubits existing in both 0 and 1 states simultaneously, enabling massive parallelism. Quantum circuits, entanglement pathways, and abstract visualizations of Shor’s and Grover’s algorithms demonstrate how quantum systems process complex problems far beyond classical capabilities. This representation highlights the transformative potential of quantum computation in cryptography, optimization, and big data analytics.

Quantum Cryptography

In Quantum Key Distribution (QKD), superposition ensures that any attempt to intercept information disturbs the quantum state, making eavesdropping detectable.

Quantum Sensors and Metrology

Devices like quantum gyroscopes and quantum clocks exploit superposition to achieve extreme precision in measurements.

This digital illustration depicts a futuristic quantum gyroscope, utilizing entangled particles and superposition to achieve ultra-precise orientation tracking. The central gyroscopic core hovers in a state of quantum balance, surrounded by glowing trajectories and probability fields that shift as the system evolves. Holographic overlays and grid structures represent quantum phase coherence, interference effects, and entanglement loops used to maintain directional accuracy. This visualization highlights how quantum technologies leverage wavefunction superposition for advanced inertial navigation systems, particularly in aerospace and submarines, where GPS-independent rotation sensing is critical.

This illustration portrays a conceptual quantum clock that leverages the principle of superposition for ultra-precise timekeeping. The central mechanism is framed by dynamic quantum waves and interference patterns, symbolizing multiple simultaneous atomic states. These overlapping states allow the quantum clock to measure time intervals with remarkable accuracy, surpassing classical atomic clocks. The design integrates quantum coherence and probabilistic phase evolution, crucial for quantum metrology and fundamental physics experiments exploring time at microscopic scales.

Experimental Evidence of Superposition

Quantum superposition is not just theoretical—it has been observed in numerous experiments:

• Double-Slit Experiment: Particles like electrons and photons exhibit interference patterns when not observed, demonstrating superposition of paths.

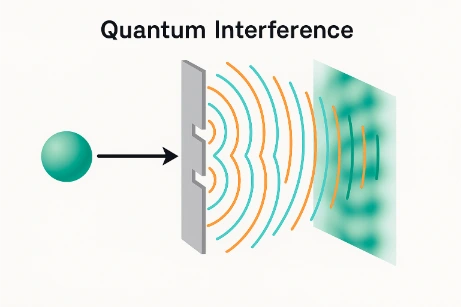
• Superconducting Circuits: Macroscopic superpositions have been observed in superconducting quantum circuits, where electric currents flow in opposite directions simultaneously.
• Interference of Large Molecules: Experiments have shown that even large molecules (like buckyballs) can exhibit superposition, suggesting the boundary between quantum and classical behavior is not yet fully understood.

Why Study Quantum Superposition in Quantum Mechanics

Foundation of Quantum Theory

Quantum superposition is one of the most fundamental principles in quantum mechanics. It asserts that a quantum system can exist in multiple states simultaneously until it is measured. This principle challenges classical notions of determinism and reality, and provides a radically different framework for understanding physical systems. Studying this concept is essential to grasping the mathematical and conceptual basis of quantum physics.

Interference and Probability Amplitudes

Superposition allows for interference between quantum states, which leads to outcomes governed by probability amplitudes rather than fixed certainties. These interference effects explain phenomena like diffraction patterns in the double-slit experiment. Understanding how amplitudes combine is critical for predicting the likelihood of measurement outcomes. This makes quantum mechanics both powerful and counterintuitive.

Wave-Particle Duality

Quantum superposition underpins the idea that particles can behave as waves and vice versa. Electrons, photons, and even larger molecules can show wave-like interference patterns when in superposed states. This duality defies classical distinctions and is a defining feature of quantum behavior. Exploring superposition helps students understand how particles exhibit both discrete and continuous properties.

Measurement and Collapse

A key aspect of superposition is that measurement causes a quantum system to collapse into a single observable state. This collapse introduces fundamental questions about the nature of observation and reality. It also plays a central role in quantum paradoxes, such as Schrödinger’s cat. Studying this process leads to a deeper appreciation of the philosophical and technical challenges in quantum theory.

Basis for Quantum Technologies

Superposition is the operational principle behind quantum technologies such as quantum computing, quantum cryptography, and quantum sensors. In a quantum computer, for instance, qubits leverage superposition to perform parallel computations. This opens up new possibilities for solving problems that are intractable for classical computers. Understanding superposition is therefore crucial for anyone interested in the future of quantum engineering and innovation.

Quantum Superposition: Conclusion

The principle of quantum superposition is central to quantum mechanics, revealing that particles can exist in multiple states until observed. It challenges classical notions of reality, causality, and determinism, raising profound philosophical questions about the nature of existence and the role of observation. This principle has been confirmed experimentally and is the foundation for revolutionary technologies like quantum computing, quantum cryptography, and quantum sensing. As research progresses, superposition continues to reshape our understanding of the universe and open doors to technologies once thought impossible. Mathematically, a quantum system is described by a wavefunction (ψ), which encapsulates all possible states the system can be in. If a quantum particle can exist in two distinct states, say ∣A⟩ and ∣B⟩, the superposition principle states that the system can be in a linear combination of these states:

∣Ψ⟩ = α∣A⟩ + β∣B⟩

Where:

∣Ψ⟩ is the superposed state.
α and β are complex probability amplitudes that determine the likelihood of the system being found in state ∣A⟩ or ∣B⟩ when measured.

The probabilities of the system being in state ∣A⟩ or ∣B⟩ are given by ∣α∣² and ∣β∣², respectively, with the condition that ∣α∣² + ∣β∣² = 1.