The structure of the atom is a foundational topic in physics, laying the groundwork for understanding matter at its most fundamental level. Within the domain of modern physics, exploring atomic structure provides insight into the arrangement and behavior of subatomic particles. The field of atomic physics closely investigates how electrons orbit the nucleus and how protons and neutrons contribute to an atom’s mass and stability.
The development of quantum theory revolutionized our understanding of the atom, leading to new models grounded in quantum mechanics. The probabilistic interpretation of electron positions, guided by the wave function and Schrödinger’s equation, replaced earlier deterministic views. Concepts like quantum superposition and quantum entanglement further deepen our understanding of atomic interactions.
To describe electron arrangements within atoms, physicists use a system of quantum numbers and electron configuration. This framework explains how electrons fill discrete energy levels and orbitals, leading to observable phenomena such as spectral lines. The distribution of electrons directly affects properties of matter studied in condensed matter physics and plays a vital role in the behavior of solids, semiconductors, and superconductors.
Atomic nuclei, composed of protons and neutrons, are governed by interactions explored in nuclear physics. Transformations within the nucleus, including nuclear fission and nuclear fusion, are central to both natural processes and technological applications. Understanding nuclear reactions and radioactivity and isotopes provides insight into atomic decay and energy release.
The atomic structure is intricately linked to the particles and forces described in particle physics. Electrons and quarks are examples of fermions (matter particles), while forces are transmitted by bosons (force carriers). These interactions fall under the domain of fundamental forces, all of which are elegantly described using quantum field theory.
Principles like Heisenberg’s uncertainty principle and wave-particle duality challenge classical intuition, but they are essential to explaining electron distributions and atomic transitions. Phenomena such as quantum tunneling arise directly from these principles and have implications ranging from semiconductor design to nuclear decay.
The atomic model also invites discussion of larger frameworks, including relativity, which becomes significant at high velocities, and statistical mechanics, which addresses behavior of atoms in large ensembles. Collectively, these perspectives enrich our appreciation for atomic structure and reveal its relevance across the sciences.
By mastering the structure of the atom, students gain the conceptual tools needed to explore everything from molecular bonding and chemical properties to nuclear energy and quantum computing. It is a central theme that connects diverse areas of physics and opens doors to deeper scientific inquiry.
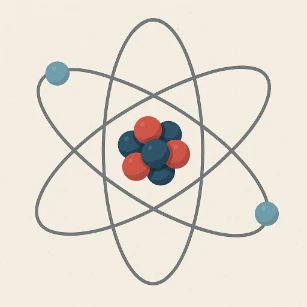
- Atomic Physics topics:
- Atomic Physics – Overview
- Structure of the Atom
- Quantum Numbers & Electron Configuration
Table of Contents
Nucleus
The nucleus is the dense central core of an atom, accounting for most of its mass. It consists of two types of subatomic particles:- Protons:
- Protons are positively charged particles.
- Each proton carries a charge of +1e (where e is the elementary charge, approximately 1.602 x 10-19 coulombs).
- The number of protons in an atom’s nucleus defines its atomic number (Z), which is crucial for determining the chemical identity of the element. For example, hydrogen has one proton (Z = 1), while carbon has six protons (Z = 6).
- Neutrons:
- Neutrons are electrically neutral particles with no charge.
- They play a key role in stabilizing the nucleus by offsetting the repulsive forces between positively charged protons.
- The number of neutrons, together with the number of protons, determines the mass number (A) of an atom. For example, carbon-12 has 6 protons and 6 neutrons, while carbon-14 has 6 protons and 8 neutrons.
- Forces in the Nucleus:
- The nucleus is held together by the strong nuclear force, which overcomes the electrostatic repulsion between protons.
- This force operates over very short distances and is one of the four fundamental forces of nature.
Electron Cloud
The electron cloud surrounds the nucleus and contains negatively charged particles called electrons.- Electrons:
- Electrons are much lighter than protons and neutrons, with a mass approximately 1/1836 of a proton’s mass.
- They carry a charge of -1e, which balances the positive charge of the protons in a neutral atom.
- Energy Levels and Shells:
- Electrons are organized in discrete energy levels or shells around the nucleus.
- These levels are labeled with n representing the principal quantum number.
- Each energy level can hold a maximum number of electrons, given by the formula 2n2. For example, the first level (n=1) can hold up to 2 electrons, the second (n = 2) up to 8, and so on.
- Electron Transitions:
- Electrons can move between energy levels by absorbing or emitting energy in the form of photons. The energy of the photon corresponds to the difference between the energy levels.
Atomic Number (Z)
The atomic number is a defining characteristic of an atom:- Represents the number of protons in the nucleus.
- Determines the element’s identity. For instance:
- Hydrogen (Z = 1) has 1 proton.
- Oxygen (Z = 8) has 8 protons.
Mass Number (A)
The mass number is the total number of protons and neutrons in the nucleus:- A=Z+N, where N is the number of neutrons.
- Mass number is often used to differentiate isotopes of an element. For example:
- Carbon-12: 6 protons + 6 neutrons (A = 12).
- Carbon-14: 6 protons + 8 neutrons (
Bohr Model (1913)
The Bohr model was a significant advancement in atomic theory:- Proposed by Niels Bohr in 1913, it built upon earlier work by Rutherford and Planck.
- Key Features:
- Electrons orbit the nucleus in fixed, circular paths called energy levels or shells.
- Electrons do not radiate energy while in a stable orbit, contrary to classical physics predictions.
- When an electron absorbs energy, it can move to a higher energy level (excitation). When it returns to a lower level, it emits energy as a photon (light quantum).
- Successes:
- Explained the emission spectra of hydrogen atoms, where electrons transition between energy levels.
- Laid the groundwork for quantum theory.
- Limitations:
- Could not explain the spectra of atoms with more than one electron.
- Did not incorporate the wave-particle duality of electrons.
Quantum Mechanical Model
The quantum mechanical model, developed in the early 20th century, replaced the Bohr model with a more accurate and comprehensive framework.- Key Concepts:
- Electrons do not travel in fixed orbits but exist in regions of probability called orbitals.
- Orbitals are defined by mathematical functions derived from Schrödinger’s equation.
- The position and momentum of an electron cannot be simultaneously determined with absolute precision (Heisenberg’s Uncertainty Principle).
- Quantum Numbers:
- Principal Quantum Number (n) : Specifies the energy level.
- Angular Momentum Quantum Number (l): Describes the shape of the orbital (s, p, d, f).
- Magnetic Quantum Number (ml): Specifies the orientation of the orbital in space.
- Spin Quantum Number (ms): Indicates the direction of the electron’s spin (+ ½ ) or (- ½ ).
- Electron Cloud:
- The quantum mechanical model visualizes electrons as forming a cloud around the nucleus, where the density of the cloud represents the likelihood of finding an electron.
- Advantages:
- Accurately describes the behavior of electrons in multi-electron atoms.
- Provides a foundation for modern chemistry, including bonding and molecular interactions.
Why Study Structure of the Atom
Fundamental Building Blocks of Matter
The structure of the atom explains how protons, neutrons, and electrons form the basis of all matter. Students explore how subatomic particles are arranged and interact within the atom. This foundational concept supports every area of chemistry and physics. Understanding atomic structure is critical for grasping the nature of the physical universe.
Historical Development and Scientific Insight
Students trace the evolution of atomic models from Dalton to Rutherford, Bohr, and quantum mechanics. This journey illustrates how scientific theories change with new evidence. It enhances appreciation for experimental physics and critical thinking. It builds a framework for understanding scientific discovery.
Forces and Energy Within the Atom
Students examine the electromagnetic forces binding electrons and the strong nuclear force in the nucleus. They analyze how energy is stored and released during nuclear reactions and electronic transitions. These principles are applied in nuclear energy, radiation, and spectroscopy. They provide a deep understanding of atomic stability and transformation.
Applications in Science and Technology
Atomic structure is key to understanding radiation, nuclear medicine, semiconductor devices, and more. Students see how atomic behavior affects material properties and biological systems. This connection supports innovation in energy, healthcare, and electronics. It demonstrates the broad relevance of atomic theory.
Link to Particle and Quantum Physics
The study of atoms leads naturally into quantum physics and subatomic particle theory. Students gain tools to analyze atomic spectra, orbital interactions, and nuclear decay. It supports progress toward advanced fields such as quantum computing and nuclear engineering. It prepares students for future exploration in fundamental science.
Structure of an Atom: Conclusion
Understanding the structure of the atom has revolutionized science, providing insights into the fundamental building blocks of matter and paving the way for advances in chemistry, physics, and technology.A comprehensive understanding of the atom’s structure has fundamentally transformed scientific knowledge, offering profound insights into the basic building blocks of matter and unlocking countless advancements across various fields. In chemistry, it has elucidated the mechanisms of chemical bonding, molecular interactions, and the periodic behavior of elements, enabling the synthesis of new materials, pharmaceuticals, and industrial compounds. In physics, it has deepened our comprehension of atomic and subatomic particles, leading to the development of quantum mechanics, nuclear energy, and particle physics.Technological innovations such as semiconductors, lasers, medical imaging, and quantum computing are direct results of applying atomic theory to real-world problems. Moreover, this understanding has driven progress in fields like nanotechnology, renewable energy, and materials science, allowing scientists and engineers to manipulate matter at the atomic and molecular levels to create revolutionary products and solutions. Ultimately, exploring the atom’s structure has not only advanced theoretical science but also profoundly impacted modern technology and industry, shaping the way we live and interact with the world today.Frequently Asked Questions: Structure of the Atom
1. What is an atom in modern physics?
In modern physics, an atom is the smallest unit of an element that retains its chemical identity. It consists of a tiny, dense nucleus containing protons and neutrons, surrounded by electrons that occupy quantised energy levels. The atom as a whole is electrically neutral when the number of electrons equals the number of protons.
2. What are the main subatomic particles and their charges?
The main subatomic particles are protons, neutrons, and electrons. Protons carry a positive electric charge, neutrons are electrically neutral, and electrons carry a negative charge. Protons and neutrons reside in the nucleus, while electrons occupy regions of space around the nucleus. The balance between positive and negative charges determines the atom’s overall charge.
3. What is the atomic number Z and what does it tell you?
The atomic number Z is the number of protons in the nucleus of an atom. It uniquely identifies an element and determines its position in the periodic table. For a neutral atom, the atomic number also equals the number of electrons, which largely controls the atom’s chemical behaviour and bonding patterns.
4. What is the mass number A and how is it different from atomic mass?
The mass number A is the total number of protons and neutrons (nucleons) in the nucleus of a particular isotope. Atomic mass, on the other hand, is the actual mass of an atom and is often given as a weighted average over the naturally occurring isotopes of an element. Mass number is always an integer, while atomic mass is usually a decimal value measured in atomic mass units.
5. What are isotopes and how do they differ from each other?
Isotopes are atoms of the same element that have the same number of protons but different numbers of neutrons. This means they share the same atomic number but have different mass numbers. Isotopes have nearly identical chemical behaviour because their electron structures are the same, but they can have different physical properties and nuclear stability, leading to stable, radioactive, or short-lived forms.
6. How did models of the atom develop from Thomson to the quantum model?
Early models, such as Thomson’s “plum pudding” model, pictured electrons embedded in a positively charged sphere. Rutherford’s scattering experiments then revealed a small, dense nucleus with electrons outside it. Bohr introduced quantised orbits to explain hydrogen’s spectrum. Finally, the quantum mechanical model replaced fixed orbits with orbitals and wavefunctions, describing electrons as probability clouds rather than tiny planets in fixed paths.
7. What is the nucleus and what forces hold it together?
The nucleus is the central core of the atom, made of positively charged protons and neutral neutrons. Although protons repel each other electrically, they are held together at very short distances by the strong nuclear force, which is much stronger than the electromagnetic force over nuclear scales. The balance between these forces and the number of neutrons determines whether a nucleus is stable or radioactive.
8. What does it mean when we say an atom is mostly empty space?
Saying an atom is mostly empty space means that the nucleus is extremely small compared to the overall size of the atom, and the electrons are spread out over a relatively large volume. If the nucleus were the size of a tiny marble, the nearest electrons would be metres away. Most of the atom’s volume is therefore not filled with solid matter, even though quantum fields and forces extend throughout this region.
9. What are electron shells and orbitals in the structure of the atom?
Electron shells are groups of energy levels labelled by the principal quantum number n, while orbitals are more detailed regions within shells where an electron is likely to be found. Orbitals are defined by quantum numbers and come in shapes such as s, p, d, and f. The arrangement of electrons in these shells and orbitals determines an atom’s chemical properties and its place in the periodic table.
10. How does atomic structure explain the periodic table and chemical behaviour?
Atomic structure explains the periodic table through the way electrons fill shells and subshells. Elements in the same group have similar valence electron configurations, leading to similar bonding patterns and reactivity. Periodic trends in properties such as ionisation energy, atomic radius, and electronegativity arise from changes in nuclear charge and the way electrons are arranged around the nucleus.
11. What is nuclear stability and how is it related to binding energy?
Nuclear stability refers to how likely a nucleus is to remain unchanged over time. It is closely related to nuclear binding energy, which is the energy required to separate a nucleus into its individual protons and neutrons. A high binding energy per nucleon usually indicates a stable nucleus, while low binding energy or certain proton–neutron ratios can lead to radioactive decay as the nucleus seeks a more stable configuration.
12. Why is understanding the structure of the atom important for students?
Understanding atomic structure gives students a foundation for many areas of physics, chemistry, and materials science. It explains the periodic table, chemical bonding, spectra, radioactivity, and the behaviour of solids, liquids, and gases at a microscopic level. This knowledge also connects directly to technologies such as lasers, semiconductors, nuclear power, medical imaging, and emerging quantum devices.
Structure of an Atom: Review Questions and Answers:
1. What is the structure of an atom?
Answer: An atom consists of a central nucleus, composed of protons and neutrons, surrounded by a cloud of electrons. This structure determines the atom’s properties and behavior in chemical interactions.
2. How is the nucleus of an atom composed?
Answer: The nucleus is made up of protons, which carry a positive charge, and neutrons, which are electrically neutral. The number of protons defines the element, while neutrons contribute to the atomic mass and stability.
3. What are electron clouds and how do they differ from fixed electron orbits?
Answer: Electron clouds represent the regions around the nucleus where electrons are likely to be found, as predicted by quantum mechanics. Unlike fixed orbits in the Bohr model, electron clouds are defined by probability distributions that indicate where an electron is most likely to be located.
4. How did the Rutherford gold foil experiment contribute to our understanding of atomic structure?
Answer: The Rutherford experiment demonstrated that most of an atom’s mass is concentrated in a small, dense nucleus. By observing the deflection of alpha particles, it disproved the plum pudding model and led to the nuclear model of the atom.
5. What is the Bohr model of the atom and what are its limitations?
Answer: The Bohr model depicts the atom as having electrons in fixed, circular orbits around the nucleus with quantized energy levels. While it successfully explained atomic spectra for hydrogen, it cannot account for the more complex behavior of multi-electron atoms or the probabilistic nature of electron locations.
6. How do quantum mechanics refine our understanding of atomic structure beyond the Bohr model?
Answer: Quantum mechanics replaces fixed orbits with electron probability clouds, using wave functions to describe electron positions and energies. This approach accounts for the uncertainty and complex interactions within atoms, offering a more accurate and comprehensive description.
7. In what way do energy levels and electron transitions determine an atom’s spectral lines?
Answer: Electrons in atoms occupy discrete energy levels. When an electron transitions between levels, it absorbs or emits a photon with energy corresponding to the difference between these levels, resulting in the characteristic spectral lines unique to each element.
8. How does electron configuration influence the chemical properties of an element?
Answer: The arrangement of electrons in various energy levels and subshells, particularly in the outermost shell, dictates how atoms interact, bond, and react with one another. This configuration underlies trends in reactivity, ionization energy, and electronegativity across the periodic table.
9. What role do quantum numbers play in describing the structure of the atom?
Answer: Quantum numbers provide a set of values that describe an electron’s energy level, orbital shape, orientation, and spin. They uniquely identify the state of an electron within an atom, thereby explaining the atom’s structure and the distribution of electrons.
10. Which modern experimental techniques are used to study the atomic structure?
Answer: Techniques such as X-ray diffraction, electron microscopy, and spectroscopy (including photoelectron spectroscopy) allow scientists to probe atomic and electronic structures. These methods provide detailed insights into atomic arrangements, bonding, and energy transitions.
Structure of an Atom: Thought-Provoking Questions and Answers
1. How can advanced imaging techniques further our understanding of the atom’s internal structure?
Answer: Advanced imaging techniques, like scanning tunneling microscopy and atomic force microscopy, enable visualization of individual atoms and electron clouds. By capturing high-resolution images, researchers can observe atomic arrangements in real time, study surface interactions, and refine theoretical models of atomic structure.
2. In what ways might the manipulation of atomic structures revolutionize material science?
Answer: Manipulating atomic structures allows for the design of materials with tailored properties such as enhanced strength, conductivity, or optical behavior. Techniques like atomic layer deposition and nanofabrication enable precise control over atomic arrangements, leading to breakthroughs in electronics, photonics, and energy storage.
3. Could a deeper understanding of electron probability clouds lead to innovations in quantum computing?
Answer: Yes, by harnessing the principles behind electron probability clouds, scientists can develop qubits that exploit superposition and entanglement. This deeper understanding may result in more stable and scalable quantum computing systems, which could dramatically outperform classical computers in certain tasks.
4. How does the uncertainty principle challenge our classical view of the atom?
Answer: The uncertainty principle states that it is impossible to precisely determine both the position and momentum of an electron simultaneously. This fundamental limit contradicts the classical notion of fixed orbits, leading to a probabilistic view of electron locations and emphasizing the need for quantum mechanical models in atomic theory.
5. What are the potential implications of altering atomic structures for energy production and storage?
Answer: Altering atomic structures at the nanoscale can improve the efficiency of energy production and storage devices. For example, engineered atomic arrangements in batteries or solar cells could lead to higher charge capacities, faster energy transfer, and improved overall performance, driving advances in renewable energy technologies.
6. How might the discovery of new subatomic particles influence our current models of atomic structure?
Answer: Discovering new subatomic particles could lead to revisions of the standard atomic model by revealing previously unknown forces or interactions within the nucleus. Such discoveries might refine our understanding of nuclear stability, electron behavior, and the fundamental building blocks of matter, potentially resulting in a new paradigm in atomic physics.
7. In what ways do electron correlations and interactions challenge the predictive power of current atomic models?
Answer: Electron correlations, which involve complex interactions between electrons, can lead to unexpected phenomena that are difficult to predict using simplified models. Accurately accounting for these correlations requires advanced computational methods and may reveal new insights into chemical reactivity, superconductivity, and other quantum effects in materials.
8. How can the study of atomic structure contribute to the development of novel pharmaceuticals and medical treatments?
Answer: A detailed understanding of atomic and molecular structures enables the design of drugs that interact precisely with biological targets. By modeling how atoms bond and interact at the molecular level, researchers can develop more effective pharmaceuticals with targeted actions and reduced side effects, advancing personalized medicine.
9. What role do relativistic effects play in the structure of heavy atoms, and how might they alter chemical properties?
Answer: In heavy atoms, relativistic effects cause inner electrons to move at speeds approaching that of light, altering orbital shapes and energy levels. These changes can significantly impact the chemical properties of heavy elements, such as their reactivity and bonding behavior, necessitating modifications to standard atomic models for accurate predictions.
10. How might emerging quantum technologies, such as ultrafast lasers, shed light on dynamic processes within the atom?
Answer: Ultrafast lasers can capture electron transitions and other rapid processes within atoms in real time, offering insights into dynamic phenomena like electron correlation and energy redistribution. These observations can validate theoretical predictions, enhance our understanding of quantum dynamics, and drive innovations in spectroscopy and photonics.
11. In what ways could future research on atomic structure influence our understanding of the origin of matter in the universe?
Answer: Future research on atomic structure can help unravel the processes that governed the formation of matter shortly after the Big Bang. By studying the fundamental interactions and energy transitions within atoms, scientists may uncover clues about nucleosynthesis, cosmic evolution, and the distribution of elements throughout the universe.
12. What ethical considerations arise from the ability to manipulate atoms at the most fundamental level?
Answer: Manipulating atoms raises ethical concerns related to potential environmental impacts, the creation of novel materials with unforeseen hazards, and the dual-use nature of advanced technologies. Responsible research and regulation are essential to ensure that atomic-scale manipulations benefit society while minimizing risks associated with their application.
Numerical Problems and Solutions
1. Calculate the Bohr radius in meters given that the Bohr radius for a hydrogen atom is approximately 0.529 Å.
Solution:
1 Å = 1 × 10⁻¹⁰ m
Bohr radius = 0.529 Å = 0.529 × 10⁻¹⁰ m = 5.29 × 10⁻¹¹ m
2. Determine the energy of an electron in the n=2 level of a hydrogen atom using the Bohr model (Eₙ = –13.6 eV/n²).
Solution:
For n=2:
E₂ = –13.6 eV / (2²) = –13.6 eV / 4 = –3.4 eV
3. Calculate the energy difference between the n=2 and n=3 levels in a hydrogen atom.
Solution:
E₂ = –13.6/4 = –3.4 eV
E₃ = –13.6/9 ≈ –1.51 eV
Energy difference ΔE = |E₂ – E₃| = |–3.4 – (–1.51)| = 1.89 eV
4. Using the energy difference from Problem 3, compute the wavelength of the photon emitted during an n=3 to n=2 transition. (Use E = hc/λ with h = 4.1357×10⁻¹⁵ eV·s and c = 3×10⁸ m/s)
Solution:
ΔE = 1.89 eV
λ = (hc)/ΔE = (4.1357×10⁻¹⁵ eV·s × 3×10⁸ m/s) / 1.89 eV
λ ≈ (1.2407×10⁻⁶ eV·m) / 1.89 eV ≈ 6.56×10⁻⁷ m or 656 nm
5. A hydrogen atom is ionized by supplying energy equal to its ionization energy (13.6 eV). Convert this energy into joules.
Solution:
1 eV = 1.602×10⁻¹⁹ J
13.6 eV = 13.6 × 1.602×10⁻¹⁹ J ≈ 2.18×10⁻¹⁸ J
6. Using the Rydberg formula, calculate the wavelength of the Lyman-alpha line (transition from n=2 to n=1) for hydrogen. (R = 1.097×10⁷ m⁻¹)
Solution:
Rydberg formula: 1/λ = R (1/1² – 1/2²) = 1.097×10⁷ (1 – 1/4) = 1.097×10⁷ × 0.75
1/λ = 8.2275×10⁶ m⁻¹
λ = 1 / 8.2275×10⁶ ≈ 1.215×10⁻⁷ m or 121.5 nm
7. If an electron in a hydrogen atom absorbs a photon and jumps from n=1 to n=3, calculate the energy of the absorbed photon.
Solution:
E₁ = –13.6 eV
E₃ = –13.6/9 ≈ –1.51 eV
Energy absorbed ΔE = E₃ – E₁ = (–1.51) – (–13.6) = 12.09 eV
8. Determine the frequency of a photon with a wavelength of 486 nm (a line in the Balmer series).
Solution:
λ = 486 nm = 486×10⁻⁹ m
Using c = 3×10⁸ m/s, frequency ν = c/λ = 3×10⁸ / (486×10⁻⁹) ≈ 6.17×10¹⁴ Hz
9. For an electron transitioning from n=4 to n=2 in a hydrogen atom, calculate the wavelength of the emitted photon using the Rydberg formula.
Solution:
1/λ = R (1/2² – 1/4²) = 1.097×10⁷ (1/4 – 1/16) = 1.097×10⁷ (0.25 – 0.0625) = 1.097×10⁷ × 0.1875 ≈ 2.057×10⁶ m⁻¹
λ = 1 / 2.057×10⁶ ≈ 4.86×10⁻⁷ m or 486 nm
10. A nucleus exerts an electrostatic force on an electron in a hydrogen atom. Using Coulomb’s law, estimate the force if the electron is at the Bohr radius (5.29×10⁻¹¹ m) with a proton charge of 1.602×10⁻¹⁹ C. (k = 8.99×10⁹ N·m²/C²)
Solution:
Force F = k·|q₁q₂|/r² = (8.99×10⁹)(1.602×10⁻¹⁹)²/(5.29×10⁻¹¹)²
= (8.99×10⁹ × 2.566×10⁻³⁸)/(2.80×10⁻²¹)
≈ (2.307×10⁻²⁸)/(2.80×10⁻²¹) ≈ 8.24×10⁻⁸ N
11. Calculate the de Broglie wavelength of an electron moving at 2.2×10⁶ m/s. (mₑ = 9.11×10⁻³¹ kg and h = 6.626×10⁻³⁴ J·s)
Solution:
λ = h / (mₑ·v) = 6.626×10⁻³⁴ / (9.11×10⁻³¹ × 2.2×10⁶)
= 6.626×10⁻³⁴ / 2.0042×10⁻²⁴ ≈ 3.31×10⁻¹⁰ m
12. For a hydrogen-like ion with nuclear charge Z = 3, compute the energy of the electron in the ground state using Eₙ = –13.6 Z²/n² (with n = 1).
Solution:
E₁ = –13.6 × (3²) / 1² = –13.6 × 9 = –122.4 eV
