Atomic physics stands at the heart of our understanding of matter and energy at the smallest scales, focusing on the properties and behaviors of atoms, particularly the structure of electrons around the nucleus. As a branch of physics, atomic physics is deeply interconnected with advances in modern physics and serves as a foundation for many applied technologies such as lasers, atomic clocks, and quantum computing. It investigates atomic spectra, energy levels, and the role of quantum numbers and electron configuration in determining atomic behavior.
The structure of the atom—including the positively charged nucleus and surrounding electron cloud—has evolved from classical planetary models to complex quantum mechanical interpretations. Tools developed in quantum mechanics, including the wave function and Schrödinger’s equation, form the basis of these explanations. Phenomena such as quantum superposition, quantum entanglement, and quantum tunneling are essential for understanding how electrons behave within atoms.
Atomic physics overlaps significantly with nuclear physics and particle physics. While atomic physics focuses on the atom as a whole, it cannot ignore nuclear processes like nuclear fission, nuclear fusion, and nuclear reactions. The concept of radioactivity and isotopes also emerges as critical in interpreting the behavior of unstable atomic nuclei.
The atom is further understood in terms of its fundamental constituents, described in fermions (matter particles) and bosons (force carriers). The interactions between these particles are governed by the fundamental forces, embedded within the mathematical structures of quantum field theory. These advanced theories are indispensable for explaining atomic transitions and fine structure effects in atomic spectra.
Atomic physics is also supported by related studies such as statistical mechanics, which helps predict macroscopic properties of matter from the statistical behavior of atomic ensembles. It links seamlessly to condensed matter physics, especially in the study of atomic lattices and electronic band structures in solids.
A key philosophical and scientific breakthrough underpinning atomic physics is the concept of Heisenberg’s uncertainty principle, which reveals intrinsic limitations in measuring atomic properties. Similarly, the idea of wave-particle duality has challenged and reshaped our view of the electron and photon as entities that defy classical categorization.
Atomic physics also intersects with large-scale phenomena explored in relativity. Although relativistic effects are more prominent in high-energy or high-speed environments, they become important in precision measurements of atomic energy levels and time dilation in satellite-based atomic clocks.
Whether through advancing our understanding of atomic transitions, enabling quantum technology, or contributing to fundamental theories of matter, atomic physics continues to be a central pillar of modern science. It links microscopic phenomena with universal principles, grounding both theoretical exploration and practical innovation.

- Atomic Physics topics:
- Atomic Physics – Overview
- Structure of the Atom
- Quantum Numbers & Electron Configuration
Exploring Atomic Physics – From Basic Structure to Quantum States
Atomic physics asks how atoms are built, how their electrons are arranged, and how those electrons move between energy levels. These ideas explain spectral lines, lasers, atomic clocks, and many modern technologies. On this hub, you move from the basic structure of the atom to the more formal language of quantum numbers and electron configurations that you will meet again in university-level physics and chemistry.
Atomic Physics – Overview
Use this page as your starting map for atomic physics. It revisits core ideas such as atoms, ions, isotopes, and energy levels, and shows how models evolved from Bohr’s picture to modern quantum theory. You will see how these concepts connect to spectroscopy, lasers, plasma physics, and solid-state physics studied elsewhere in Prep4Uni.Online.
Structure of the Atom
Focuses on how atoms are put together: nuclei, electrons, and the forces that bind them. This page walks through historical models, electron orbits versus orbitals, and the idea of quantised energy levels. It prepares you for understanding spectra, ionisation energy, and why different elements have distinct chemical and physical behaviour.
Quantum Numbers & Electron Configuration
Introduces the quantum numbers that label electron states and the rules used to fill atomic orbitals (Pauli exclusion, Hund’s rule, and Aufbau principles). You will see how electron configurations underpin the periodic table, magnetism, selection rules in spectroscopy, and the design of devices such as lasers and magnetic-resonance systems.
Table of Contents
Fundamental Concepts in Atomic Physics
Structure of the Atom
- Nucleus: Dense core composed of protons (positive charge) and neutrons (neutral charge).
- Electron Cloud: Surrounds the nucleus, composed of negatively charged electrons orbiting in discrete energy levels.
- Atomic Number (Z): Number of protons, defining the chemical element.
- Mass Number (A): Sum of protons and neutrons.
- Introduced quantized energy levels for electrons, explaining atomic spectra.
- Electrons orbit the nucleus in fixed paths without radiating energy and can jump between orbits by absorbing or emitting photons.
- Replaced Bohr’s model with a probabilistic framework.
- Electrons exist in orbitals, described by quantum numbers rather than fixed orbits.

Quantum Numbers and Electron Configuration
Electrons in atoms are described by four quantum numbers:- Principal Quantum Number (n): Energy level or shell (n = 1, 2, 3, …).
- Angular Momentum Quantum Number (l): Subshell (s, p, d, f) determining the shape of the orbital.
- Magnetic Quantum Number (mₗ): Orientation of the orbital in space.
- Spin Quantum Number (s): Direction of the electron’s spin (+½ or -½).
- Describes the distribution of electrons among orbitals.
- Example for Oxygen: 1s² 2s² 2p⁴.
Key Topics in Atomic Physics
Atomic Spectra and Energy Levels
- Atomic Spectra: Unique patterns of light emitted or absorbed by atoms when electrons transition between energy levels.
- Emission Spectrum: Produced when electrons drop from higher to lower energy levels, emitting photons.
- Absorption Spectrum: Occurs when electrons absorb specific photon energies to jump to higher energy states.
- Simplest atomic spectrum with distinct series: Lyman (UV), Balmer (visible), and Paschen (IR).
- Explained using the Rydberg formula:
Electron Transitions and Photon Emission
- Absorption: Electrons absorb photons with energy matching the difference between two energy levels (
- Emission: Electrons release energy as photons when dropping to lower levels.
- Spontaneous Emission: Occurs naturally without external influence.
- Stimulated Emission: Triggered by external photons, leading to laser operation.
Ionization and Atomic Collisions
- Ionization: Removal of one or more electrons from an atom, forming an ion.
- First Ionization Energy: Energy required to remove the first electron.
- Multiple Ionizations: Higher energies needed to remove subsequent electrons.
- Atomic Collisions: Interactions between atoms and particles (e.g., electrons, photons, ions).
- Elastic Collisions: Kinetic energy is conserved.
- Inelastic Collisions: Energy is transferred, causing excitation or ionization.
Zeeman and Stark Effects
- Zeeman Effect: Splitting of atomic spectral lines in a magnetic field due to magnetic interaction with electron spins.
- Stark Effect: Splitting of spectral lines in an electric field due to the distortion of electron orbitals.
Applications of Atomic Physics
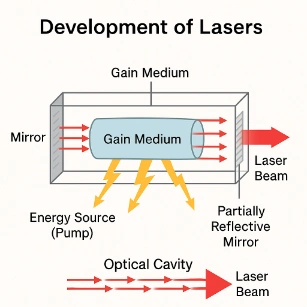
Development of Lasers
Laser (Light Amplification by Stimulated Emission of Radiation):- Based on controlled electron transitions.
- Uses stimulated emission to amplify coherent light.
- Gain Medium: Provides the environment for electron transitions (e.g., ruby, gas, semiconductors).
- Energy Source (Pump): Excites electrons to higher energy states.
- Optical Cavity: Reflects photons to stimulate further emissions.
- Medical: Eye surgery (LASIK), cancer treatment, tissue welding.
- Industrial: Cutting, welding, 3D printing.
- Communication: Fiber optic data transmission.
Spectroscopic Techniques for Chemical Analysis
Spectroscopy involves studying how atoms and molecules interact with electromagnetic radiation.- Absorption Spectroscopy: Measures light absorbed by atoms to identify substances.
- Emission Spectroscopy: Analyzes light emitted by excited atoms.
- Fluorescence Spectroscopy: Detects light emitted by atoms after absorbing energy.
- Astronomy: Identifying elements in stars.
- Environmental Science: Detecting pollutants.
- Medicine: Analyzing blood and tissue samples.
Atomic Clocks
- Rely on precise electron transitions in atoms like cesium and rubidium.
- The current definition of a second is based on cesium’s transition frequency.
- Applications include GPS, telecommunications, and fundamental physics research.
Quantum Computing and Quantum Information
- Uses principles of superposition and entanglement in atomic systems.
- Trapped ions and neutral atoms are leading platforms for building quantum bits (qubits).
- Offers exponentially faster computation for complex problems.
Advanced Topics in Atomic Physics
Fine and Hyperfine Structure
- Fine Structure: Splitting of atomic energy levels due to electron spin-orbit coupling.
- Hyperfine Structure: Further splitting caused by interactions between the nuclear spin and the electron cloud.
Bose-Einstein Condensates (BECs)
- A state of matter where atoms cooled to near absolute zero occupy the same quantum state.
- Predicted by Bose and Einstein, first realized in 1995 with rubidium atoms.
Rydberg Atoms
- Highly excited atoms with electrons in very high energy levels.
- Extremely sensitive to electric and magnetic fields, useful for quantum simulations.
Challenges and Future Directions in Atomic Physics
- Quantum Control of Atomic Systems:
- Improving precision in controlling and manipulating single atoms for quantum technologies.
- Atom-Photon Interaction:
- Enhancing light-matter interactions for better quantum communication and sensing.
- Fusion Energy:
- Understanding ion collisions and plasma behavior to develop practical nuclear fusion reactors.
- Fundamental Physics Tests:
- Using atomic transitions to test fundamental symmetries and constants of nature.
Why Study Atomic Physics
Exploring the Structure and Behavior of Atoms
Atomic physics focuses on the properties and interactions of atoms, particularly the behavior of electrons around the nucleus. Students examine how atomic models evolved and how spectra are formed. This provides a detailed understanding of atomic structure and transitions. It lays the groundwork for quantum mechanics and chemical bonding.
Quantum Models and Spectral Analysis
Students study Bohr’s model, quantum energy levels, and electronic transitions that produce spectral lines. These concepts help explain the behavior of matter at the microscopic scale. Spectral analysis is used in laboratories, astronomy, and diagnostics. It illustrates the power of atomic theory in explaining physical phenomena.
Experimental Techniques and Instrumentation
Students learn how to use spectroscopy, electron beams, and lasers to probe atomic structure. These hands-on techniques are essential in physics, chemistry, and engineering. Practical skills in measurement and analysis strengthen scientific competency. They prepare students for laboratory research and industrial applications.
Applications in Technology and Energy
Atomic physics supports advancements in nuclear power, atomic clocks, and quantum sensors. Students explore how atomic precision impacts GPS, communication, and medical imaging. Understanding atoms enables control over matter and energy at the smallest scales. It drives progress in technology and fundamental science.
Bridge to Quantum and Molecular Physics
Atomic physics leads naturally into studies of quantum mechanics, molecular physics, and condensed matter. Students gain a comprehensive view of how atoms combine, interact, and form complex systems. This continuity enriches scientific understanding and interdisciplinary learning. It provides a strong foundation for careers in science and engineering.
Conclusion on Atomic Physics
Atomic physics is a cornerstone of modern science, providing critical insights into the behavior of matter and energy at the atomic scale. It has revolutionized our understanding of:- Atomic structure and electron dynamics
- Photon emission and light-matter interaction
- Quantum principles underlying modern technology
Frequently Asked Questions: Atomic Physics
1. What is atomic physics?
Atomic physics is the branch of modern physics that studies the structure and behaviour of isolated atoms, especially the arrangement and motion of electrons around the nucleus. It focuses on topics such as energy levels, spectra, ionisation, and how atoms interact with light and external fields.
2. How is atomic physics different from nuclear physics?
Atomic physics concentrates on the electrons bound to an atomic nucleus and how they determine the atom’s energy levels, spectra, and chemical behaviour. Nuclear physics, by contrast, studies the protons and neutrons inside the nucleus itself, along with nuclear forces, radioactivity, and nuclear reactions. In short, atomic physics is mainly about electrons, while nuclear physics is mainly about the nucleus.
3. What is meant by atomic energy levels and electron shells?
Atomic energy levels are the discrete allowed energies that an electron can have when it is bound to an atom. Electrons occupy shells and subshells associated with these levels, rather than having a continuous range of energies. When an electron moves between energy levels, the atom must absorb or emit a photon with an energy equal to the difference between the levels.
4. What is an atomic spectrum and why is it discrete?
An atomic spectrum is the set of wavelengths of light that an atom emits or absorbs when electrons make transitions between quantised energy levels. Because these levels are discrete rather than continuous, only certain photon energies are allowed, leading to a series of sharp lines in the spectrum rather than a smooth band. Each element has a unique line spectrum that acts like a fingerprint.
5. How did the Bohr model contribute to atomic physics?
The Bohr model proposed that electrons orbit the nucleus in specific allowed orbits with quantised angular momentum, and that radiation is emitted or absorbed only when an electron jumps between these orbits. It successfully explained the main spectral lines of hydrogen and introduced the idea of quantised energy levels, paving the way for modern quantum mechanics, even though later models replaced its planetary picture.
6. How does quantum mechanics describe electrons in atoms?
Quantum mechanics describes electrons in atoms using wavefunctions and probability distributions rather than fixed orbits. Solutions of the Schrödinger equation for the hydrogen atom lead to orbitals, which are regions of space where an electron is likely to be found. Quantum numbers label these orbitals and determine properties such as energy, angular momentum, and spin orientation.
7. What are quantum numbers and what do they represent in atomic physics?
Quantum numbers are a set of integers and half-integers that label the allowed quantum states of an electron in an atom. The principal quantum number relates to energy and shell, the orbital quantum number to the shape of the orbital, the magnetic quantum number to orientation, and the spin quantum number to the electron’s intrinsic spin. Together, they specify the electron configuration and help explain the structure of the periodic table.
8. What is ionisation energy and why is it important?
Ionisation energy is the minimum energy required to remove an electron completely from a gaseous atom in its ground state. It reflects how strongly the electron is bound to the nucleus and varies systematically across the periodic table. Ionisation energies are crucial for understanding chemical reactivity, plasma formation, and the conditions in stellar atmospheres and laboratory plasmas.
9. How do external electric and magnetic fields affect atomic energy levels?
External electric fields (Stark effect) and magnetic fields (Zeeman effect) can shift and split atomic energy levels. These perturbations change the energies of the electron states, leading to small shifts or splittings in spectral lines. Studying these effects allows physicists to probe fine details of atomic structure, measure field strengths, and test quantum theories with high precision.
10. What is fine structure and hyperfine structure in atomic spectra?
Fine structure refers to small splittings of atomic energy levels caused by relativistic corrections and spin–orbit coupling, where the electron’s spin interacts with its orbital motion. Hyperfine structure arises from interactions between the magnetic moments of the nucleus and the electrons. These subtle effects produce additional closely spaced lines in atomic spectra and are important in precision spectroscopy and atomic clocks.
11. Where is atomic physics applied in modern technology?
Atomic physics underlies technologies such as gas discharge lamps, lasers, atomic clocks, and many types of sensors. It is central to spectroscopy used in chemical analysis, astronomy, and environmental monitoring. Atomic physics principles are also vital in plasma devices, fusion research, semiconductor processing, and emerging quantum technologies based on trapped ions and neutral atoms.
12. Why should students learn atomic physics before university?
Learning atomic physics before university introduces students to the quantum picture of matter in a concrete, visual way. It connects the periodic table, chemical bonding, and spectral lines to underlying physical principles, and prepares students for more advanced courses in quantum mechanics, solid-state physics, and spectroscopy. It also shows how abstract quantum ideas translate into real devices and measurements.
Atomic Physics: Review Questions and Answers:
1. What is atomic physics and why is it a crucial branch of modern physics?
Answer: Atomic physics studies the structure and behavior of atoms, including their electrons, nuclei, and the forces that bind them. It is crucial because it forms the basis for understanding matter at the microscopic level and underpins technologies such as lasers and semiconductors.
2. What are the key quantum models used to describe atomic structure?
Answer: The key quantum models include the Bohr model, which introduces quantized electron orbits, and the quantum mechanical model, which uses probability distributions and wave functions to describe electron positions. These models explain the discrete energy levels observed in atoms.
3. How does the Bohr model explain electron transitions and spectral lines?
Answer: In the Bohr model, electrons occupy fixed orbits with specific energy levels. When electrons transition between these levels, they absorb or emit energy in discrete amounts, producing characteristic spectral lines. This quantization accounts for the observed line spectra in atomic emission.
4. What is an emission spectrum and how does it relate to atomic structure?
Answer: An emission spectrum is the set of wavelengths emitted by excited atoms as their electrons return to lower energy levels. Each element has a unique emission spectrum, which reflects its discrete energy levels and serves as a fingerprint for identifying elements.
5. How does spectroscopy aid in the study of atomic physics?
Answer: Spectroscopy analyzes the interaction between light and matter by examining the absorption or emission of light at specific wavelengths. It allows scientists to determine atomic energy levels, study electron transitions, and identify the elemental composition of substances.
6. What role did Rutherford’s experiments play in shaping our understanding of atomic structure?
Answer: Rutherford’s gold foil experiment revealed that atoms have a small, dense, positively charged nucleus surrounded by electrons. This discovery replaced the earlier plum pudding model and paved the way for the development of nuclear and quantum theories in atomic physics.
7. How is energy quantization significant in atomic physics?
Answer: Energy quantization means that electrons can only exist in discrete energy levels. This concept is essential for explaining why atoms absorb or emit energy in fixed amounts, leading to the formation of unique spectral lines and influencing chemical behavior.
8. What is the significance of electron wave functions in the quantum mechanical model of the atom?
Answer: Electron wave functions describe the probability distribution of an electron’s position and momentum. They replace the idea of fixed orbits with regions of likelihood, offering a more accurate representation of atomic behavior and predicting phenomena such as electron cloud shapes and chemical bonding.
9. How does atomic physics contribute to modern technological advancements?
Answer: Atomic physics underpins technologies like lasers, semiconductor devices, nuclear energy, and medical imaging. Its principles enable the design of devices that rely on precise control of electron behavior and energy quantization, driving innovation in various high-tech fields.
10. What are some current challenges or open questions in the field of atomic physics?
Answer: Current challenges include achieving a deeper understanding of electron correlation effects, accurately modeling complex atomic interactions, and integrating atomic physics with quantum computing and nanotechnology. These challenges drive ongoing research to refine theoretical models and experimental techniques.
Atomic Physics: Thought-Provoking Questions and Answers
1. How might advances in quantum computing transform our approach to solving atomic physics problems?
Answer: Advances in quantum computing could enable simulations of atomic systems with unprecedented precision by leveraging quantum bits to model electron interactions and energy states. This would allow for solving complex many-body problems that are currently intractable on classical computers, potentially leading to breakthroughs in material science and chemistry.
2. In what ways could a deeper understanding of electron correlation improve the accuracy of atomic models?
Answer: A deeper understanding of electron correlation would allow scientists to better predict electron interactions within atoms and molecules, leading to more accurate models of atomic behavior. This could enhance our ability to design new materials, optimize chemical reactions, and improve the accuracy of spectroscopic analysis in various scientific fields.
3. How can modern spectroscopic techniques be used to explore exotic states of matter at the atomic level?
Answer: Modern spectroscopic techniques, such as ultrafast laser spectroscopy and X-ray spectroscopy, can capture transient states and high-energy processes in atoms. These techniques enable the study of exotic states like Bose-Einstein condensates or Rydberg atoms, providing insights into quantum phase transitions and the behavior of matter under extreme conditions.
4. What potential breakthroughs could arise from reconciling quantum mechanical models with relativistic effects in atomic physics?
Answer: Reconciling quantum mechanics with relativistic effects could lead to a more unified theory that accurately describes high-speed particles and heavy atoms. This breakthrough would improve our understanding of atomic nuclei, predict new particles or interactions, and potentially lead to innovations in nuclear medicine, energy production, and particle physics.
5. How might emerging experimental techniques reshape our understanding of electron dynamics in atoms?
Answer: Emerging experimental techniques, such as attosecond pulse lasers and advanced electron microscopy, allow scientists to observe electron dynamics in real time. These methods can reveal how electrons move and interact on extremely short timescales, leading to refined models of electron behavior and a better grasp of quantum phenomena at the atomic level.
6. In what ways could insights from atomic physics influence the development of new energy sources?
Answer: Insights from atomic physics, particularly in nuclear interactions and energy quantization, can drive the development of more efficient nuclear reactors or fusion energy sources. Understanding the atomic-scale processes governing energy release and absorption could lead to safer, cleaner, and more sustainable energy technologies.
7. How might atomic physics contribute to advancements in medical imaging and cancer treatment?
Answer: Atomic physics underlies techniques such as positron emission tomography (PET) and magnetic resonance imaging (MRI), which rely on nuclear magnetic properties and radioactive decay. Further research could lead to more precise imaging methods and targeted radiation therapies, improving early diagnosis and treatment outcomes in oncology.
8. What role does the study of atomic physics play in understanding the origins of the universe?
Answer: The study of atomic physics provides insights into the formation of the first atoms and the evolution of matter after the Big Bang. By examining spectral lines and energy levels from distant celestial objects, scientists can trace the chemical evolution of the universe, understand star formation, and study the processes that led to the creation of galaxies.
9. How could the manipulation of atomic states lead to breakthroughs in data storage and information processing?
Answer: Manipulating atomic states through techniques like laser cooling and trapping can lead to the development of atomic clocks and quantum memory devices. These breakthroughs have the potential to revolutionize data storage and processing by offering extremely precise timekeeping and the ability to harness quantum states for high-speed, low-energy information processing.
10. What challenges arise when attempting to measure electron positions and energies in atoms with high precision?
Answer: Measuring electron positions and energies is challenged by the uncertainty principle, which limits simultaneous precision in determining these properties. Additionally, electron interactions and environmental perturbations can obscure measurements, necessitating advanced experimental setups and sophisticated statistical models to achieve high accuracy.
11. How might new discoveries in atomic physics alter our understanding of chemical bonding and reactions?
Answer: New discoveries in atomic physics, particularly regarding electron correlation and quantum behavior, could redefine the theories of chemical bonding. Improved models may explain reaction mechanisms more accurately, leading to innovations in catalysis, material synthesis, and the development of new chemical processes with greater efficiency and selectivity.
12. How can interdisciplinary research involving atomic physics lead to innovative technologies in areas like nanotechnology and materials science?
Answer: Interdisciplinary research that integrates atomic physics with nanotechnology and materials science can lead to the design of novel materials with tailored electronic, optical, and mechanical properties. Understanding atomic-scale interactions allows for the engineering of materials at the nanoscale, fostering breakthroughs in electronics, photonics, and biomedical applications.
Atomic Physics: Numerical Problems
Below are twelve numerical problems, each followed by a step-by-step solution.
(Math is written in LaTeX. I have removed commands that often trigger “Undefined control sequence”, such as \dfrac and \boxed.)
1. Hydrogen Energy Transition (\(n=3 \to n=2\))
Question: In a hydrogen atom, the energy difference between the \(n=3\) and \(n=2\) levels is approximately \(1.89\,\mathrm{eV}\). Calculate the wavelength of the photon emitted during this transition.
Solution:
Use \(E=\frac{hc}{\lambda}\), so \(\lambda=\frac{hc}{E}\).
Convert energy to joules:
\[ E = 1.89 \times 1.602 \times 10^{-19} \approx 3.03 \times 10^{-19}\,\mathrm{J}. \]
Substitute values:
\[ \lambda = \frac{(6.626\times 10^{-34})(3.0\times 10^{8})}{3.03\times 10^{-19}} \approx 6.56\times 10^{-7}\,\mathrm{m} = 656\,\mathrm{nm}. \]
Answer: \(\lambda \approx 656\,\mathrm{nm}\)
2. Bohr Radius for \(n=2\)
Question: Using the Bohr model, calculate the radius of the \(n=2\) orbit if \(r_1=0.0529\,\mathrm{nm}\).
Solution:
Bohr radius formula: \(r_n=n^2r_1\).
\[ r_2 = 2^2(0.0529) = 0.2116\,\mathrm{nm}. \]
Answer: \(r_2 \approx 0.212\,\mathrm{nm}\)
3. Ionisation Energy of Hydrogen
Question: Determine the ionisation energy of a hydrogen atom in the ground state.
Solution:
Ionisation energy is the energy required to remove the electron from \(n=1\) to infinity.
Answer: \(13.6\,\mathrm{eV}\)
4. Balmer Line at \(486\,\mathrm{nm}\)
Question: A hydrogen emission line is observed at \(486\,\mathrm{nm}\). Identify the electronic transition.
Solution:
Balmer-series lines end at \(n=2\):
\[ \frac{1}{\lambda} = R\left(\frac{1}{2^2}-\frac{1}{n^2}\right). \]
The line at \(486\,\mathrm{nm}\) corresponds to \(n=4\).
Answer: \(n=4 \to n=2\)
5. Energy of a \(121.6\,\mathrm{nm}\) Photon
Question: Calculate the energy of a photon with wavelength \(121.6\,\mathrm{nm}\).
Solution:
\[ E=\frac{hc}{\lambda} = \frac{(6.626\times10^{-34})(3.0\times10^{8})}{121.6\times10^{-9}} \approx 1.63\times10^{-18}\,\mathrm{J}. \]
Convert to eV:
\[ E \approx \frac{1.63\times10^{-18}}{1.602\times10^{-19}} \approx 10.2\,\mathrm{eV}. \]
Answer: \(E \approx 10.2\,\mathrm{eV}\)
6. Ground-State Energy of a Hydrogen-Like Ion (\(Z=3\))
Question: Find the ground-state energy for a hydrogen-like ion with \(Z=3\).
Solution:
Energy levels:
\[ E_n = -13.6\,\frac{Z^2}{n^2}\,\mathrm{eV}. \]
For \(n=1\):
\[ E_1 = -13.6(3^2) = -122.4\,\mathrm{eV}. \]
Answer: \(E_1=-122.4\,\mathrm{eV}\)
7. Energy Released (\(n=5 \to n=3\))
Question: An electron falls from \(n=5\) to \(n=3\). Calculate the energy released.
Solution:
\[ E_5 = -\frac{13.6}{25} = -0.544\,\mathrm{eV},\qquad E_3 = -\frac{13.6}{9} \approx -1.51\,\mathrm{eV}. \]
\[ \Delta E = |E_3 - E_5| = |-1.51 - (-0.544)| \approx 0.967\,\mathrm{eV}. \]
Answer: \(\Delta E \approx 0.97\,\mathrm{eV}\)
8. Photon Absorption from \(n=2\)
Question: A hydrogen atom absorbs a \(12.09\,\mathrm{eV}\) photon while in \(n=2\). What happens?
Solution:
Initial energy:
\[ E_2 = -\frac{13.6}{2^2} = -3.4\,\mathrm{eV}. \]
After absorption:
\[ E_f = E_2 + 12.09 = -3.4 + 12.09 = 8.69\,\mathrm{eV}. \]
Since \(E_f>0\), the electron becomes unbound.
Answer: Ionisation occurs.
9. Photon Frequency (\(n=3 \to n=2\))
Question: Find the frequency of the photon emitted for the \(n=3 \to n=2\) transition if \(E=1.89\,\mathrm{eV}\).
Solution:
Convert to joules:
\[ E = 1.89 \times 1.602 \times 10^{-19} \approx 3.03 \times 10^{-19}\,\mathrm{J}. \]
Use \(\nu=\frac{E}{h}\):
\[ \nu = \frac{3.03\times10^{-19}}{6.626\times10^{-34}} \approx 4.57\times10^{14}\,\mathrm{Hz}. \]
Answer: \(\nu \approx 4.6\times10^{14}\,\mathrm{Hz}\)
10. Wavelength (\(n=4 \to n=2\))
Question: Determine the wavelength for the hydrogen transition \(n=4 \to n=2\).
Solution:
\[ \frac{1}{\lambda} = R\left(\frac{1}{2^2}-\frac{1}{4^2}\right) = R\left(\frac{1}{4}-\frac{1}{16}\right) = R\frac{3}{16}. \]
This is the Balmer H-β line.
Answer: \(\lambda \approx 486\,\mathrm{nm}\)
11. Cascade Transition (Two Photons)
Question: Hydrogen emits two photons in a cascade and ends at \(n=2\). Give one plausible cascade path.
Solution:
One common two-step cascade that ends at \(n=2\) is:
\[ n=4 \to n=3 \to n=2. \]
Answer: One plausible cascade is \(4 \to 3 \to 2\).
12. He+ Transition (\(Z=2,\; n=3 \to n=2\))
Question: Calculate the wavelength for the transition \(n=3 \to n=2\) in the hydrogen-like ion He+ (\(Z=2\)).
Solution:
Energy difference (in eV):
\[ \Delta E = 13.6 Z^2\left(\frac{1}{2^2}-\frac{1}{3^2}\right) = 13.6(4)\left(\frac{1}{4}-\frac{1}{9}\right). \]
\[ \Delta E = 54.4\left(\frac{5}{36}\right) \approx 7.56\,\mathrm{eV}. \]
Use \(hc \approx 1240\,\mathrm{eV\cdot nm}\), so \(\lambda \approx \frac{1240}{\Delta E}\):
\[ \lambda \approx \frac{1240}{7.56}\,\mathrm{nm} \approx 164\,\mathrm{nm}. \]
Answer: \(\lambda \approx 164\,\mathrm{nm}\)
