The First Law of Motion, also known as the Law of Inertia, marks a defining moment in the development of physics and continues to serve as a foundational principle in understanding motion. It states that an object will remain at rest or move with constant velocity unless acted upon by a net external force. This deceptively simple idea, introduced by Isaac Newton, underpins the broader structure of classical mechanics and introduces students to the conceptual shift from Aristotelian to Newtonian thought.
The implications of the First Law extend into various branches of mechanics. In dynamic frameworks, this law sets the stage for studying forces and accelerations, while in kinematics it defines the context for uniform motion in the complete absence of a net force. The transition to subsequent balance equations builds directly upon this initial baseline, forming a coherent framework for predicting the behavioral evolution of physical mass distributions.
Explorations in rigid body pathways and statics often reference the First Law when analyzing absolute static equilibrium or mapping the initial onset of motion. Similarly, when calculating responses in vibrations and oscillations, the role of starting configurations and net restoring force vectors becomes clearer when framed through the lens of inertia. This law also informs how continuous mediums behave under stress, such as in fluid mechanics and continuum mechanics, where internal resistance to shear or displacement must be overcome to initiate macroscopic flow.
More advanced mathematical treatments, like those found in analytical mechanics, extend the concept of inertia to generalized coordinates and elegant Lagrangian action formulations, offering a deeper and more abstract appreciation of the First Law’s global significance. Meanwhile, in celestial tracking models, this law is highly evident in the trajectories of planets, comets, and asteroids, which continue along predictable orbital paths unless perturbed by external gravitational force vectors.
As we delve into modern physics, relativistic mechanics refines our understanding of inertia by incorporating the speed of light as an absolute limiting velocity factor, redefining how objects in motion respond to force inputs at high speeds. This modification has critical implications in astrophysical systems, high-energy environments, and the ionized particle paths tracked in plasma physics.
The First Law also directly intersects with the fundamentals of electricity and magnetism, where isolated charged particles remain stationary or maintain uniform linear motion in the absence of external electromagnetic fields. As soon as external fields are introduced—such as those studied in electrostatics, magnetic fields, and electrodynamics—the target particles immediately deviate from their background inertial paths. This physical deviation is strictly governed by localized force interactions, reinforcing Newton’s fundamental baseline insights.
Concepts such as electromagnetic induction and electromagnetic waves depend on understanding the transition from ideal inertial states to forced, time-dependent behavior. Within electrical circuits, mechanical inertia has a direct mathematical analog in the form of inductive and capacitive storage effects, where the electrical current naturally resists sudden changes in flux, reflecting Newton’s law perfectly.
Advanced engineering fields like magnetohydrodynamics (MHD) and magnetostatics continue to explore how inertia and magnetic force fields interact inside dynamic plasmas and steady-state magnetic arrays. Across all physical domains, Newton’s First Law stands as the primary gateway to understanding how forces influence matter, anchoring the universal physical laws that govern both everyday phenomena and extraordinary technology.
Statement of Newton’s First Law of Motion
- Inertia – The intrinsic tendency of an object to resist any change to its instantaneous state of motion.
- Balanced and Unbalanced Forces – A system’s velocity profile remains completely unchanged unless influenced by an external, net non-zero force vector.
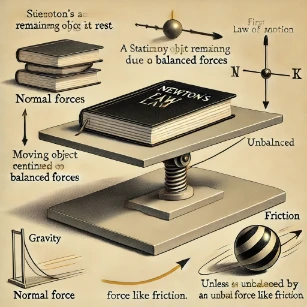
Table of Contents
Understanding the Concept of Inertia
The Mechanical Property of Inertia
- A more massive object possesses a larger measure of inertia, meaning it demands a significantly larger external force vector field to disrupt its current trajectory or alter its state of velocity.
- A less massive object has diminished inertia, allowing it to be accelerated or decelerated with far less external energy input.
Distinction Between Balanced and Unbalanced Forces
- Balanced Forces: This condition occurs when the vector sum of all external forces acting on a body evaluates exactly to zero. Because the force vectors cancel each other out entirely, the system maintains dynamic equilibrium.Example: A textbook resting flat on a lecture table experiences a downward gravitational load that is perfectly counteracted by the solid surface’s upward normal force vector.
- Unbalanced Forces: This occurs when the net vector sum of all concurrent forces is non-zero. This net force breaks the system’s equilibrium state and acts as the direct mathematical driver of acceleration.Example: Applying an intense horizontal push to a stalled vehicle overcomes local friction boundaries, generating a net force that forces the vehicle to accelerate forward.
Real-World Applications and Examples
Automobile Seatbelts and Restraint Dynamics
The Classic Tablecloth Inertia Experiment
Spacecraft Flight Paths and Free Fall Trajectories
Mathematical Representation of Newton’s First Law
$$\sum \mathbf{F} = 0$$
$$\mathbf{a} = 0$$
- ∑F = The net vector sum of all concurrent external forces acting on the target object.
- a = The resulting acceleration vector of the mass system.
$$\mathbf{v}(t) = \mathbf{v}_0 = \text{Constant}$$
- If the initial velocity vector was zero ($$\mathbf{v}_0 = 0$$), the object remains completely at rest.
- If the object possessed an active velocity vector ($$\mathbf{v}_0 \neq 0$$), it will continue moving at a constant speed along a perfectly straight line path.
The Historical Evolution of Motion Theory
From Aristotelian Mechanics to Newtonian Relativity
| Scientific Era | Core Paradigm of Motion | The Role of Force |
|---|---|---|
| Aristotelian (c. 350 BCE) | Matter naturally seeks absolute rest. Continuous motion requires a continuous physical pusher. | Force is the immediate cause of velocity ($$F \propto v$$). If force stops, motion ceases instantly. |
| Galilean (c. 1632 CE) | Introduced the concept of frictionless planes. Matter naturally preserves its state of motion. | Force is only required to alter a trajectory or overcome surface resistance. |
| Newtonian (1687 CE) | Formalized the First Law of Motion. Established the mathematical baseline of Inertial Reference Frames. | Force is the immediate cause of acceleration ($$\mathbf{F} = m\mathbf{a}$$), changing momentum states over time. |
Inertia Thought Experiment Laboratory
Grasping Ideal Systems Beyond Earthbound Observations
1. Galileo’s Inverted Double-Incline Track
Imagine a perfectly frictionless, U-shaped marble track. If you release a marble from the top of the left incline, it rolls down and climbs up the right incline until it reaches the exact same vertical height from which it started.
Now, imagine lowering the angle of the right-hand incline so it is shallower. The marble must travel a much further linear distance along the slope to reach its target matching height. Finally, what happens if you lower the right side completely flat to a horizontal plain? Because the marble can never climb to reach its original baseline elevation, it must roll forward along the straight line path indefinitely at a constant velocity.
2. Einstein’s Co-Moving Interplanetary Elevator
Consider an enclosed windowless laboratory cabin coasting deep in interstellar space. If a researcher releases a mass marker, it floats stationary in mid-air because the net force vector on both the room and the mass equals zero.
However, if an external tether cable suddenly yanks the cabin upward with a constant acceleration rate, the floor slams up toward the floating mass marker. To the researcher trapped inside, the object appears to “fall” to the floor with an apparent acceleration. This highlights the absolute necessity of Newton’s first constraint: we can only evaluate true force fields if our coordinate frame itself is non-accelerating (an Inertial Frame).
Numerical Examples of Newton’s First Law of Motion
Example 1: A Stationary Object in Static Equilibrium
$$\sum \mathbf{F} = 0$$
Solution:
Because the net force vector field evaluates to zero, the system’s acceleration must also equal zero:
$$\mathbf{a} = \frac{\sum \mathbf{F}}{m} = 0 \text{ m/s}^2$$
Since the box started from rest ($$\mathbf{v}_0 = 0$$), its state of motion cannot change over time.
Example 2: Constant Velocity Motion Profiles
$$m = 1\,200 \text{ kg}$$
Solution:
Because the vehicle moves at a constant speed in a perfectly straight line, its velocity vector is invariant over time, meaning its acceleration matches zero:
$$\mathbf{a} = \frac{d\mathbf{v}}{dt} = 0 \text{ m/s}^2$$
Substituting this acceleration parameter into the classical force balance relation:
$$\sum \mathbf{F} = m \cdot \mathbf{a} = 1\,200 \times 0 = 0 \text{ Newtons}$$
Example 3: Transition to Forced Acceleration Limits
$$m = 5 \text{ kg}$$
Solution:
Prior to the force application, the system followed the First Law, maintaining a constant velocity vector because the net force was zero. Once the 10 N force is introduced, an unbalanced state is established, triggering active linear acceleration:
$$a = \frac{F_{\text{net}}}{m} = \frac{10}{5} = 2 \text{ m/s}^2$$
The Role of Non-Conservative Dissipation Forces
- Mechanical Friction: Microscopic structural surface contact features generate resistance parallel to the interface plane, actively removing mechanical kinetic energy from sliding systems.
- Fluid Air Resistance: As an object travels through the atmosphere, collisions with air molecules generate a fluid drag force field that increases with velocity, counteracting the system’s forward momentum.
Common Misconceptions About Newton’s First Law
- Misconception: Continuous forces are required to sustain steady-state motion.Reality: This is an illusion caused by environment friction. An object requires a net force to change its velocity, not to maintain it. In a vacuum, motion requires no force inputs to persist.
- Misconception: Heavier mass bodies naturally move faster than lighter mass systems.Reality: Mass dictates inertia, which is strictly a resistance parameter against acceleration. An object’s mass does not determine its baseline coasting velocity vector.
Why Study the First Law of Motion
Foundation of Classical Mechanics
Concept of Inertia and Mass
Applications in Everyday Life
Role in Friction and Equilibrium
Preparation for Further Study
Newton’s First Law of Motion: Conclusion
First Law of Motion — FAQ
What is the first law of motion?
The first law of motion states that an object will remain at rest or move at a constant velocity in a straight line unless acted upon by a net external force. This law defines the concept of inertia and describes the natural state of motion for an object in the absence of unbalanced forces.
Who formulated the first law of motion and why is it important?
The first law of motion is attributed to Sir Isaac Newton, and it's important because it establishes the principle of inertia — showing that motion does not require a continuous force to be maintained. Instead, force is needed only to change motion, which underpins all classical dynamics.
What does 'net external force' mean in the context of the first law?
A net external force refers to the vector sum of all external forces acting on an object. If all external forces cancel out (net force is zero), the object’s motion will not change. If there is a non-zero net external force, the object’s state of motion can change — it may accelerate, decelerate or change direction.
Can an object move at constant velocity if forces are acting on it?
Yes — provided that the forces on the object balance out so the net external force is zero. In such a case, even though individual forces act, their effects cancel, and the object continues moving at constant velocity as if no force is present.
How does the first law relate to inertia and inertial frames?
Inertia is the tendency of an object to resist changes in its state of motion — that is, to keep moving with constant velocity or remain at rest. A frame of reference in which the first law holds (objects at rest or in uniform motion remain so when no net force acts) is called an inertial frame. The first law defines and justifies the use of inertial frames in physics.
What are common misconceptions about the first law of motion?
A common misconception is that a force is required to keep an object moving at constant speed; in fact, no force is needed if motion is uniform and the net force is zero. Another misconception is confusing mass with weight: mass is a measure of inertia, not a force.
How does friction affect the application of the first law in everyday life?
Friction is an external force that opposes motion. In everyday life, it prevents objects from continuing at constant velocity once the initial force is removed, causing them to slow down and eventually stop. This gives the impression — incorrectly — that constant force is needed to maintain motion, but the first law shows that without friction (or other net external forces), motion would continue indefinitely.
Does the first law apply in non-inertial (accelerating) frames of reference?
The first law strictly holds only in inertial frames — frames that are either at rest or moving at constant velocity. In non-inertial (accelerating) frames, observers may observe apparent forces (fictitious forces), so the first law does not hold in its simple form unless those pseudo-forces are included.
How is the first law used to simplify physics problems?
The first law helps identify when net force is zero, so one can conclude that velocity is constant (or the object is at rest) without solving complicated equations. It allows use of equilibrium or constant-velocity assumptions to simplify analysis before applying more detailed force or energy methods.
Why is the concept of inertia central to understanding motion in physics?
Inertia captures the idea that objects resist changes in their motion. Without inertia, motion and rest would not be distinguishable. Recognizing inertia helps understand why force is necessary to change motion, but not to maintain it — which is a foundational insight for all of classical mechanics.
How does the first law connect to everyday observations like a sliding object coming to rest?
In everyday life, sliding objects often come to rest when the push is removed because friction (or air resistance) acts as an external force opposing motion. The first law explains that in the absence of net external force (if friction were zero), the object would continue sliding forever at constant velocity — but real-world forces change that ideal behavior.
How does the first law pave the way for the second and third laws?
The first law defines the natural behavior of objects when no net force acts — constant velocity or rest. The second law builds on this by quantifying how motion changes when a net force is present (F = ma). The third law ensures that forces come in pairs, maintaining consistency when forces arise from interactions. Together, the three laws form a complete foundation for classical dynamics.
Can the first law of motion be tested experimentally, and how?
Yes — by observing motion in situations where external forces are negligible (e.g., frictionless air tracks, nearly friction-free wheels, or in outer space). If an object continues moving at constant velocity without any applied force, that supports the first law. Demonstrations such as a puck gliding on a nearly frictionless surface or a spacecraft coasting demonstrate the law in practice.
Newton’s First Law of Motion: Review Questions
- What is Newton’s First Law of Motion?Answer: Newton’s First Law, also known as the law of inertia, states that an object at rest will remain at rest and an object in motion will continue moving at constant velocity unless acted upon by a net external force.
- How does the concept of inertia relate to the First Law of Motion?Answer: Inertia is the inherent resistance of an object to any change in its state of motion. The First Law illustrates inertia by showing that without an external force, an object’s velocity remains unchanged.
- What does it mean for an object to be in equilibrium according to the First Law?Answer: An object is in equilibrium when the net external force acting on it is zero. In this state, if the object is at rest it remains at rest, and if it is moving, it continues with constant velocity.
- How does the First Law of Motion apply to objects at rest?Answer: For objects at rest, the First Law implies that they will not move unless a net external force is applied. Their state of rest is maintained by inertia.
- How does the First Law of Motion apply to objects in motion?Answer: For objects already in motion, the law states that they will continue moving in a straight line at constant speed unless a net external force causes a change in speed or direction.
- What role do external forces play in changing an object’s state of motion?Answer: External forces are necessary to overcome an object’s inertia and change its state of motion, whether by accelerating, decelerating, or changing its direction.
- How can friction be considered as an external force in the context of the First Law?Answer: Friction is an external force that opposes motion. It acts to decelerate moving objects or to prevent motion from starting, thereby demonstrating that a net force is required to maintain or change an object’s state of motion.
- How does the concept of inertia explain the resistance of objects to changes in motion?Answer: Inertia explains that objects resist changes to their motion due to their mass. A heavier object has more inertia and therefore requires a greater force to change its state of motion compared to a lighter object.
- What are some real-life examples that illustrate the First Law of Motion?Answer: Examples include a book resting on a table, remaining at rest until moved, and a hockey puck gliding on ice, continuing in motion with little friction. In both cases, a net external force is needed to alter their state.
- How does Newton’s First Law lay the foundation for the other laws of motion?Answer: The First Law establishes the concept of inertia and the need for an external force to change motion. This understanding is crucial for developing Newton’s Second Law: $$F = ma$$ and Third Law, which describes action-reaction interactions.
Newton’s First Law of Motion: Thought-Provoking Questions
- How might the concept of inertia be reinterpreted in a universe with different fundamental forces?Answer: In a universe with altered fundamental forces, inertia might depend on additional factors such as interactions with a pervasive field or modified mass properties. This could lead to variations in how objects resist motion changes and may require new theoretical frameworks that extend or modify Newton’s classic definition.
- What implications would arise if an object in motion could spontaneously change direction without an external force?Answer: A spontaneous change in direction without an external force would contradict the First Law, suggesting a violation of momentum conservation. It would prompt a major rethinking of classical mechanics and could indicate the presence of unknown internal forces or quantum effects at macroscopic scales.
- How does the First Law of Motion influence the design of safety features in vehicles?Answer: Understanding inertia helps engineers design safety systems such as seat belts, airbags, and crumple zones that counteract sudden changes in motion during collisions. These features manage the forces on passengers by extending the time over which deceleration occurs, thereby reducing injury.
- In what ways can the concept of equilibrium from the First Law be applied to economic or social systems?Answer: Equilibrium in economics or social systems refers to a state where forces or influences balance out, leading to stability. Just as an object remains at rest or moves uniformly when net forces are zero, markets or societies may stabilize when opposing factors, such as supply and demand or social pressures, are in balance.
- How does our understanding of inertia evolve with advancements in quantum mechanics?Answer: Quantum mechanics introduces probabilistic behavior and wave-particle duality, which may influence how inertia is understood at microscopic scales. This could lead to a deeper insight into how mass and resistance to motion emerge from quantum interactions, potentially refining the classical concept of inertia.
- What are the limitations of applying the First Law of Motion to objects moving at relativistic speeds?Answer: At speeds approaching the speed of light, relativistic effects such as time dilation and mass-energy changes become significant. The First Law still holds, but the classical definitions of force, mass, and acceleration must be modified to account for these relativistic phenomena, requiring Einstein’s theory of relativity for accurate predictions.
- How does the First Law of Motion relate to the conservation of momentum in isolated systems?Answer: The First Law implies that without external forces, an object’s momentum remains constant. This is the basis for the conservation of momentum, which states that the total momentum of an isolated system is conserved, forming a cornerstone of both classical and modern physics.
- Could there be experimental conditions under which the First Law appears to be violated, and how might these be explained?Answer: Apparent violations could occur in systems with unaccounted-for forces, such as electromagnetic interactions or air currents. Alternatively, in quantum systems, the probabilistic nature of particles might seem to defy classical expectations, but these cases are resolved by recognizing that different laws govern microscopic scales.
- How does our everyday intuition about motion get challenged by the counterintuitive aspects of the First Law?Answer: Everyday experiences often mask the persistence of motion due to friction and other forces, making the First Law seem less obvious. For example, in space, an object will continue moving indefinitely without resistance, which can be counterintuitive compared to Earth-bound experiences where friction is omnipresent.
- What are the key differences between centrifugal and centripetal effects in circular paths?Answer: Centripetal force is a real inward force acting on an object to maintain a curved path. In contrast, centrifugal effects are apparent outward pushes experienced only from within a rotating reference frame, directly resulting from the object’s linear inertia trying to continue in a straight line.
- What role does the First Law play in the development of modern propulsion systems, such as those used in spacecraft?Answer: The First Law underlies the principle that, in the vacuum of space, a spacecraft will continue moving at a constant velocity unless acted upon by an external force. This concept is critical in designing propulsion systems that carefully manage thrust to achieve precise maneuvers while conserving fuel.
- How might experimental methods be improved to test the limits of the First Law in extreme environments, such as microgravity or deep space?Answer: Advanced sensors, long-duration space experiments, and high-precision tracking can improve testing of the First Law in microgravity. By minimizing external disturbances and using sophisticated data analysis, researchers can explore the nuances of inertia and verify that the law holds under conditions far removed from Earth’s surface.
Numerical Problems and Solutions
- Problem: An object rests on a frictionless surface. Find its acceleration given the tracking variables:$$m = 5 \text{ kg}, \quad F = 10 \text{ N}$$ Solution:
Applying Newton’s Second Law: $$a = \frac{F}{m} = \frac{10}{5} = 2.0 \text{ m/s}^2$$ Answer: $$2.0 \text{ m/s}^2$$ - Problem: A vehicle moves at a constant speed before a braking mechanism introduces a sudden deceleration force. Find the magnitude of this deceleration parameter given:$$m = 1\,200 \text{ kg}, \quad v_0 = 20 \text{ m/s}, \quad F_{\text{brake}} = 2\,400 \text{ N}$$ Solution:
Isolating the linear acceleration value: $$a = \frac{F}{m} = \frac{2\,400}{1\,200} = 2.0 \text{ m/s}^2$$ Answer: $$2.0 \text{ m/s}^2$$ acting opposite to the direction of motion. - Problem: An object starting from rest experiences a net horizontal force field over a brief time window. Find its final velocity profile given:$$m = 2 \text{ kg}, \quad F = 8 \text{ N}, \quad t = 3 \text{ s}$$ Solution:
First, evaluate the uniform acceleration state: $$a = \frac{F}{m} = \frac{8}{2} = 4.0 \text{ m/s}^2$$
Now map the change in velocity from a static starting index: $$v = a \cdot t = 4.0 \times 3 = 12.0 \text{ m/s}$$ Answer: $$12.0 \text{ m/s}$$ - Problem: An object experiencing uniform motion enters a region with a strong resistive counter-force. Find the exact time slice required to bring the system to rest:$$m = 10 \text{ kg}, \quad v_0 = 15 \text{ m/s}, \quad F_{\text{resistive}} = 30 \text{ N}$$ Solution:
Isolating the deceleration constraint: $$a = \frac{F}{m} = \frac{30}{10} = 3.0 \text{ m/s}^2$$
Calculate the time window required to zero out the initial velocity: $$t = \frac{v_0}{a} = \frac{15}{3.0} = 5.0 \text{ seconds}$$ Answer: $$5.0 \text{ s}$$ - Problem: A hockey puck travels with a constant velocity profile across an ideal frictionless surface workspace. Find the total net force acting on the system body given:$$m = 0.2 \text{ kg}$$ Solution:
According to the conceptual laws of Newton’s First Law, maintaining a constant velocity profile dictates that acceleration must equal zero: $$\mathbf{a} = 0 \text{ m/s}^2$$ $$\mathbf{F}_{\text{net}} = m \cdot \mathbf{a} = 0.2 \times 0 = 0 \text{ Newtons}$$ Answer: $$0 \text{ N}$$ - Problem: A system body experiences zero net external force loading across a short time interval. Find its net change in velocity given:$$m = 3 \text{ kg}, \quad t = 10 \text{ s}$$ Solution:
If the net force vector field evaluates identically to zero, the acceleration profile satisfies zero change: $$\mathbf{a} = 0 \text{ m/s}^2$$ $$\Delta \mathbf{v} = \mathbf{a} \cdot t = 0 \times 10 = 0 \text{ m/s}$$ Answer: $$\Delta v = 0 \text{ m/s}$$ - Problem: A moving block encounters a continuous counterforce acting directly opposite to its velocity vector trajectory. Find its final velocity state after a fixed duration given:$$m = 50 \text{ kg}, \quad v_0 = 8 \text{ m/s}, \quad F = 100 \text{ N}, \quad t = 4 \text{ s}$$ Solution:
Evaluate the deceleration field vector: $$a = \frac{F}{m} = \frac{100}{50} = 2.0 \text{ m/s}^2$$
Subtract the accumulated deceleration profile from the starting state vector: $$v = v_0 – a \cdot t = 8 – (2.0 \times 4) = 8 – 8 = 0 \text{ m/s}$$ Answer: $$0 \text{ m/s}$$ (the system is brought to a complete stop). - Problem: A structural element receives a localized mechanical impulse. Find its absolute change in velocity given:$$m = 1 \text{ kg}, \quad \text{Impulse } (J) = 5 \text{ N}\cdot\text{s}$$ Solution:
By the definitions of the impulse-momentum theorem: $$J = \Delta p = m \cdot \Delta v$$ $$\Delta v = \frac{J}{m} = \frac{5}{1} = 5.0 \text{ m/s}$$ Answer: $$5.0 \text{ m/s}$$ - Problem: A constant linear force field acts on a system in identical orientation to its starting velocity path. Find its new velocity profile after a short duration window given:$$m = 3 \text{ kg}, \quad v_0 = 10 \text{ m/s}, \quad F = 6 \text{ N}, \quad t = 2 \text{ s}$$ Solution:
Calculate the active acceleration rate: $$a = \frac{F}{m} = \frac{6}{3} = 2.0 \text{ m/s}^2$$
Evaluate the velocity integration step: $$v = v_0 + a \cdot t = 10 + (2.0 \times 2) = 10 + 4 = 14.0 \text{ m/s}$$ Answer: $$14.0 \text{ m/s}$$ - Problem: An object moves along an active trajectory field. If the net force vector field evaluates identically to zero, find its final velocity parameter after a long duration:$$m = 4 \text{ kg}, \quad v_0 = 12 \text{ m/s}, \quad t = 5 \text{ s}$$ Solution:
According to Newton’s First Law, a mass system continues along its current motion profile at a constant speed if no net force disrupts its state. The velocity parameter remains completely invariant over time. Answer: $$12.0 \text{ m/s}$$
Mechanics Through the Lens of Inertia and Reference Frames
Mechanics – Overview
Establishes the full structure of motion and force.
First Law of Motion
Defines inertia and inertial reference frames.
Kinematics
Uses inertial frames for motion description.
Dynamics
Introduces forces that break inertial motion.
Second Law of Motion
Quantifies deviations from inertial behavior.
Third Law of Motion
Maintains interaction balance in inertial systems.
Statics
Represents a special inertial case of equilibrium.
Rigid Body Dynamics
Applies inertia to rotational systems.
Analytical Mechanics
Embeds inertia in generalized coordinates.
Celestial Mechanics
Uses inertial frames for orbital prediction.
Relativistic Mechanics
Redefines inertia in spacetime contexts.
Fluid Mechanics
Applies inertia to flowing media.
Continuum Mechanics
Extends inertia across continuous matter fields.
Vibrations & Oscillations
Shows inertia within periodic motion systems.