Prepare for University Studies & Career Advancement

Thermodynamic Cycles

Thermodynamic Cycles

Thermodynamic cycles are foundational to understanding how energy conversion systems operate, particularly in engines, power plants, refrigerators, and air conditioners. These cycles describe a sequence of processes involving heat and work transfer, typically returning the system to its initial state. Grounded in the principles of thermodynamics, these cycles showcase the application of the laws of thermodynamics and serve as essential models in mechanical and chemical engineering. Whether analyzing the Carnot, Otto, Diesel, or Rankine cycles, the thermodynamic approach offers deep insights into system efficiency and entropy changes.

The theoretical underpinnings of thermodynamic cycles are best appreciated through a solid grasp of classical thermodynamics. These cycles often involve idealized processes such as isothermal expansion or adiabatic compression, simplifying the system for deeper analytical clarity. Students engaged in engineering thermodynamics routinely apply these models to evaluate real-world performance, optimize fuel consumption, and design sustainable energy systems.

Recent developments have led to the use of computational thermodynamics to simulate complex, real-time processes in thermodynamic cycles. These simulations account for transient heat transfer, variable pressure-volume relationships, and fluid dynamics. Such integrations are also necessary for understanding heat transfer within cycle components like condensers, evaporators, and turbines, especially when working across large temperature gradients.

Beyond equilibrium assumptions, thermodynamic cycles intersect with the domain of non-equilibrium thermodynamics, which deals with irreversible processes and real-world inefficiencies. Additionally, phenomena like phase transitions within cycles (e.g., liquid-vapor transitions in steam turbines) are governed by fundamental thermodynamic relationships and material properties.

The microscopic basis for the operation of thermodynamic cycles is provided by statistical thermodynamics, which explains how aggregate properties like temperature and entropy emerge from molecular-level interactions. This connection is particularly helpful when dealing with advanced cycles in nanotechnology and aerospace systems. It also complements the behavior of working substances in diverse contexts, as explored in thermodynamics of materials.

Thermodynamic cycles are closely related to developments in renewable and sustainable energy, where optimizing energy extraction from sources like solar, wind, and geothermal is crucial. For instance, organic Rankine cycles are employed in low-temperature geothermal energy systems. Understanding these processes requires fluency in core topics such as physics, modern physics, and even specialized areas like atomic physics when working at high-energy or nanoscale levels.

Applications of thermodynamic cycles can also be found in advanced energy technologies like nuclear fusion and nuclear reactions, where control of heat and radiation is paramount. Topics like radioactivity and isotopes also become relevant when dealing with radioactive working fluids or decay heat removal in nuclear power cycles.

Supporting theoretical frameworks from quantum mechanics and wave-particle duality enhance our understanding of microstate transitions and energy level populations, particularly in cutting-edge technologies like quantum heat engines. Broader physical theories such as relativity and electrodynamics become significant when designing systems operating at high velocities or in charged environments, as in plasma physics.

In essence, thermodynamic cycles form the analytical core for numerous technologies across multiple energy platforms. From science fundamentals to practical engineering, they unify theory and application in ways that profoundly influence both conventional and emerging technologies.

 
An illustration of thermodynamic cycles, depicting a steam turbine (Rankine cycle), an internal combustion engine (Otto cycle), and a refrigeration system (vapor compression cycle) with energy flow visualization.
An illustration of thermodynamic cycles, depicting a steam turbine (Rankine cycle), an internal combustion engine (Otto cycle), and a refrigeration system (vapor compression cycle) with energy flow visualization.

Table of Contents

Basic Concepts in Thermodynamic Cycles

Working Substance

The medium (usually a gas or vapor) that undergoes the thermodynamic processes in the cycle. Examples include steam, air, and refrigerants.

Heat Reservoirs

Sources or sinks of heat energy:

  • Hot reservoir: Supplies heat to the system.
  • Cold reservoir: Absorbs waste heat from the system.

Processes in Cycles

Typical thermodynamic processes involved include:

  • Isothermal (constant temperature)
  • Adiabatic (no heat transfer)
  • Isobaric (constant pressure)
  • Isochoric/Isometric (constant volume)
Four-part illustration showing thermodynamic processes—Isothermal, Adiabatic, Isobaric, and Isochoric—with P-V graphs.
Visual comparison of four key thermodynamic processes: Isothermal (constant temperature), Adiabatic (no heat exchange), Isobaric (constant pressure), and Isochoric (constant volume). Each process is depicted with a P-V diagram.

Net Work Output

Since the cycle returns to its initial state, the internal energy change is zero (ΔU = 0) . Thus, the net work done equals the net heat added:

Wnet=Qin−QoutW_{\text{net}} = Q_{\text{in}} – Q_{\text{out}}

Thermal Efficiency (η)

For heat engines:

η=WnetQin=1−QoutQin\eta = \frac{W_{\text{net}}}{Q_{\text{in}}} = 1 – \frac{Q_{\text{out}}}{Q_{\text{in}}}

For refrigerators and heat pumps:

COPrefrigerator=QLWnet,COPheat pump=QHWnet\text{COP}_{\text{refrigerator}} = \frac{Q_L}{W_{\text{net}}}, \quad \text{COP}_{\text{heat pump}} = \frac{Q_H}{W_{\text{net}}}

Types of Thermodynamic Cycles

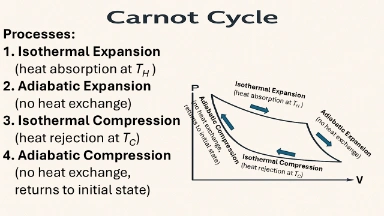
Carnot Cycle

Theoretical, idealized cycle that represents the maximum possible efficiency for a heat engine operating between two temperatures.

Processes:

  1. Isothermal Expansion (heat absorption at TH )
  2. Adiabatic Expansion (no heat exchange)
  3. Isothermal Compression (heat rejection at TC)
  4. Adiabatic Compression (no heat exchange, returns to initial state)
Diagram of the Carnot Cycle showing a four-segment closed loop on a pressure-volume (P–V) graph, illustrating the idealized heat engine cycle
The Carnot Cycle represents the most efficient theoretical heat engine cycle, illustrated here as a closed loop in a pressure-volume diagram.

Efficiency:

ηCarnot=1−TCTH\eta_{\text{Carnot}} = 1 – \frac{T_C}{T_H}

Significance:

  • Sets the upper limit of efficiency for all heat engines.
  • Completely reversible but impractical due to ideal assumptions.

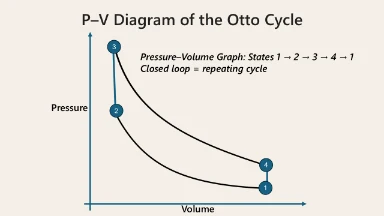
Otto Cycle

Model of Spark-Ignition Internal Combustion Engines (used in gasoline cars).

Processes:

  • Adiabatic Compression
  • Isochoric Heat Addition (combustion)
  • Adiabatic Expansion (power stroke)
  • Isochoric Heat Rejection

Efficiency:

ηOtto=1−1rγ−1\eta_{\text{Otto}} = 1 – \frac{1}{r^{\gamma – 1}}

Where:

r = compression ratio

γ = heat capacity ratio

Significance:
Higher compression ratios yield better efficiency but can cause engine knocking.

A pressure-volume (P–V) diagram of the Otto Cycle, showing a closed loop with two curved adiabatic processes and two vertical isochoric processes, modeling a gasoline engine cycle.
The Otto Cycle models the idealized thermodynamic process of a spark-ignition internal combustion engine, consisting of adiabatic compression and expansion, and isochoric heat addition and rejection.

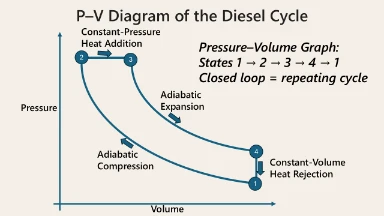
Diesel Cycle

Model of Compression-Ignition Engines (used in diesel engines).

Processes:

  1. Adiabatic Compression
  2. Isobaric Heat Addition (combustion)
  3. Adiabatic Expansion
  4. Isochoric Heat Rejection

Efficiency:

ηDiesel=1−1rγ−1⋅ργ−1γ(ρ−1)\eta_{\text{Diesel}} = 1 – \frac{1}{r^{\gamma – 1}} \cdot \frac{\rho^{\gamma} – 1}{\gamma(\rho – 1)}

Where:

r = compression ratio

ρ = cutoff ratio (volume ratio during combustion)

Significance:
Diesel engines are more efficient than Otto engines due to higher compression ratios.

Diesel Engine Cycle Pressure Vs Volume Diagram
Diesel Engine Cycle Pressure Vs Volume Diagram

Rankine Cycle

Used in Steam Power Plants.

Processes:

  1. Isentropic Compression (pump)
  2. Isobaric Heat Addition (boiler)
  3. Isentropic Expansion (turbine)
  4. Isobaric Heat Rejection (condenser)

Efficiency:

ηRankine=Wturbine−WpumpQin\eta_{\text{Rankine}} = \frac{W_{\text{turbine}} – W_{\text{pump}}}{Q_{\text{in}}}

Significance:
Widely used in electricity generation using steam turbines.

Brayton Cycle

Used in Gas Turbines and Jet Engines.

Processes:

  1. Isentropic Compression (compressor)
  2. Isobaric Heat Addition (combustion)
  3. Isentropic Expansion (turbine)
  4. Isobaric Heat Rejection

Efficiency:

ηBrayton=1−1rp(γ−1)/γ\eta_{\text{Brayton}} = 1 – \frac{1}{r_p^{(\gamma – 1)/\gamma}}

Where rp is the pressure ratio.

Significance:
Important for aviation propulsion and power generation.

Numerical Examples on Thermodynamic Cycles

Example 1: Carnot Efficiency

Problem:
A Carnot engine operates between TH = 600 K and TC = 300K. Find its efficiency.

Solution:

ηCarnot=1−TCTH=1−300600=0.5\eta_{\text{Carnot}} = 1 – \frac{T_C}{T_H} = 1 – \frac{300}{600} = 0.5

The efficiency is 50%.

Example 2: Otto Cycle Efficiency

Problem:
An Otto engine has a compression ratio of 8 and γ = 1.4. Find its efficiency.

Solution:

ηOtto=1−181.4−1=1−180.4≈1−0.396=0.604\eta_{\text{Otto}} = 1 – \frac{1}{8^{1.4 – 1}} = 1 – \frac{1}{8^{0.4}} \approx 1 – 0.396 = 0.604

Answer:
The efficiency is 60.4%.

Example 3: Diesel Cycle Efficiency

Problem:
A Diesel engine has r = 18 and ρ =2. Find its efficiency (Υ = 1.4).

Solution:

ηDiesel=1−1180.4⋅21.4−11.4(2−1)≈0.65\eta_{\text{Diesel}} = 1 – \frac{1}{18^{0.4}} \cdot \frac{2^{1.4} – 1}{1.4(2 – 1)} \approx 0.65

Answer:
The efficiency is 65%.

Example 4: Rankine Cycle Efficiency

Problem:
A Rankine cycle absorbs 2000 kJ and rejects 800 kJ. Find the efficiency.

Solution:

ηRankine=2000−8002000=0.6\eta_{\text{Rankine}} = \frac{2000 – 800}{2000} = 0.6

Answer:
The efficiency is 60%.

Example 5: Brayton Cycle Efficiency

Problem:
A Brayton cycle has a pressure ratio of 10 and Υ = 1.4.

Solution:

ηBrayton=1−110(0.4/1.4)≈0.526\eta_{\text{Brayton}} = 1 – \frac{1}{10^{(0.4/1.4)}} \approx 0.526

Answer:
The efficiency is 52.6%.

Conceptual Questions and Answers on Thermodynamic Cycles

Question 1: Why is the Carnot cycle considered the most efficient cycle for converting heat into work? Answer: The Carnot cycle is the most efficient because it operates through completely reversible processes (both isothermal and adiabatic) and experiences no entropy generation or energy loss. Its efficiency depends solely on the temperatures of the heat reservoirs: ηCarnot=1−TCTH No real engine can surpass the Carnot efficiency because real processes are irreversible and involve energy losses due to friction, heat transfer, and other factors.
Question 2: Why is the efficiency of the Otto cycle lower than that of the Carnot cycle operating between the same temperature limits? Answer: The Otto cycle involves irreversible processes such as rapid compression and expansion, friction, and heat losses. Additionally, heat transfer in the Otto cycle occurs at variable temperatures, unlike the Carnot cycle, which absorbs and rejects heat at constant temperatures. This makes the Otto cycle less efficient than the ideal Carnot cycle.
Question 3: How does increasing the compression ratio affect the efficiency of an Otto cycle engine? Answer: Increasing the compression ratio ( r ) increases the efficiency of an Otto cycle because it raises the pressure and temperature during the power stroke, leading to more work output: ηOtto=1−1rγ−1\eta_{\text{Otto}} = 1 – \frac{1}{r^{\gamma – 1}} However, excessively high compression ratios can cause engine knocking, limiting how much the ratio can be increased.
Question 4: Why do Diesel engines have higher thermal efficiency than gasoline engines (Otto cycle)? Answer: Diesel engines have higher efficiency because they operate with a higher compression ratio and use isobaric heat addition. The high compression ratio allows Diesel engines to extract more work from the same amount of fuel. Additionally, the fuel is injected and combusted at high pressure, improving energy conversion efficiency.
Question 5: What is the significance of the Rankine cycle in power generation? Answer: The Rankine cycle is the standard cycle for steam power plants. It efficiently converts heat energy from fuel combustion or nuclear reactions into mechanical work using steam to drive turbines. Its design allows the use of condensers and boilers to manage heat transfer and improve efficiency in large-scale electricity generation.
Question 6: Why is regeneration used in the Rankine cycle, and how does it improve efficiency? Answer: Regeneration in the Rankine cycle involves using steam extracted from the turbine to preheat the feedwater entering the boiler. This process reduces the amount of fuel needed to heat the water to its boiling point, lowering the heat input required and increasing the overall thermal efficiency of the cycle.
Question 7: How does the Brayton cycle differ from the Rankine cycle in terms of working fluid and applications? Answer: The Brayton cycle uses a gas (typically air) as the working fluid, whereas the Rankine cycle uses steam. The Brayton cycle is primarily used in gas turbines for aviation propulsion and electricity generation, while the Rankine cycle is common in steam power plants. The Brayton cycle operates on isobaric heat addition and isentropic expansion/compression, while the Rankine cycle involves phase changes (liquid to vapor and back).
Question 8: Why can’t real engines achieve the theoretical efficiency predicted by their thermodynamic cycles? Answer: Real engines cannot achieve theoretical efficiency due to several practical factors:
  • Frictional losses in moving parts.
  • Heat losses due to imperfect insulation.
  • Irreversible processes like rapid combustion and expansion.
  • Mechanical limitations in design and materials. These imperfections lead to entropy generation and energy dissipation, lowering the actual efficiency below the ideal predictions of thermodynamic cycles.

Why Study Thermodynamic Cycles

Modeling Practical Energy Systems

Thermodynamic cycles describe the sequence of processes by which heat engines and refrigeration systems operate. Students study ideal and real cycles to understand how energy is transformed and transferred. This analysis enables performance assessment and design optimization. It is fundamental for mechanical and energy engineering.

Ideal Cycles: Carnot, Otto, and Brayton

Students explore ideal cycles that represent the theoretical limits of system efficiency. These include Carnot for maximum thermal efficiency, Otto for spark-ignition engines, and Brayton for jet turbines. These models serve as benchmarks for practical systems. They clarify key ideas like compression ratios and thermal efficiency.

Real Cycle Considerations and Losses

Real-world cycles involve irreversibilities such as friction, pressure drops, and heat loss. Students analyze these effects to improve designs and troubleshoot inefficiencies. This supports development of advanced engines, compressors, and expanders. It bridges theory and practice in system development.

Cooling and Heat Pump Cycles

Students study cycles like vapor-compression and absorption refrigeration. These are critical in food preservation, air conditioning, and climate control. Understanding thermodynamic behavior allows for system sizing and energy saving. It supports environmental sustainability through efficient cooling technologies.

Relevance to Power and Environmental Systems

Thermodynamic cycles are at the heart of power plants, desalination systems, and waste heat recovery. Students explore how to harness energy more sustainably and cleanly. This connects their learning to current environmental and technological needs. It builds expertise for careers in clean energy and sustainable engineering.

 

Conclusion on Thermodynamic Cycles

Thermodynamic cycles are critical for converting energy into useful work and for designing efficient energy systems. Understanding cycles like the Carnot, Otto, Diesel, Rankine, and Brayton helps engineers develop advanced technologies in transportation, power generation, and refrigeration. By analyzing and optimizing these cycles, we can improve energy efficiency and sustainability in modern industries.

Thermodynamics Cycles: Review Questions and Answers:

1. What is a thermodynamic cycle, and why is it important in engineering applications?
Answer: A thermodynamic cycle is a sequence of thermodynamic processes that transfer heat and work into and out of a system, ultimately returning it to its original state. These cycles are critical in engineering applications because they allow for the conversion of thermal energy into mechanical work in engines and power plants, as well as the removal of heat in refrigeration systems. By analyzing and optimizing these cycles, engineers can improve energy efficiency, reduce fuel consumption, and enhance system performance. The study of thermodynamic cycles helps in designing more sustainable energy solutions, such as hybrid and renewable power generation systems.

2. What are the main types of thermodynamic cycles, and how do they differ in function?
Answer: The main types of thermodynamic cycles are power cycles and refrigeration cycles. Power cycles, such as the Rankine, Otto, Diesel, and Brayton cycles, convert heat into mechanical work and are used in power plants and internal combustion engines. Refrigeration cycles, such as the vapor compression cycle and absorption refrigeration cycle, work in reverse, using mechanical energy to transfer heat from a lower-temperature region to a higher-temperature region, as seen in refrigerators and air conditioners. The fundamental difference between these two types is the direction of heat transfer and whether the objective is to produce work or remove heat.

3. How does the Carnot cycle establish the upper limit of efficiency for any thermodynamic cycle?
Answer: The Carnot cycle represents an idealized thermodynamic cycle that establishes the maximum possible efficiency for heat engines operating between two temperature reservoirs. It consists of two isothermal and two adiabatic processes and assumes no entropy generation or irreversibilities such as friction and heat losses. The efficiency of the Carnot cycle is given by η = 1 – (T_C / T_H), where T_C is the temperature of the cold reservoir and T_H is the temperature of the hot reservoir. Since all real-world cycles involve irreversibilities, their efficiency is always lower than the theoretical maximum predicted by the Carnot cycle.

4. What are the key processes involved in the Rankine cycle, and how does it improve the efficiency of power plants?
Answer: The Rankine cycle is a widely used thermodynamic cycle in steam power plants and consists of four main processes: (1) Isentropic compression in the pump, (2) Heat addition in the boiler, (3) Isentropic expansion in the turbine, and (4) Heat rejection in the condenser. This cycle improves efficiency by using water as the working fluid and employing high-pressure steam to generate mechanical work in turbines. To further enhance efficiency, regenerative and reheat Rankine cycles are employed, reducing entropy generation and improving heat recovery, making modern power plants more energy-efficient.

5. How do internal combustion engine cycles like Otto and Diesel cycles differ in operation?
Answer: The Otto cycle, used in gasoline engines, and the Diesel cycle, used in diesel engines, are both internal combustion engine cycles but differ in their fuel ignition process. The Otto cycle operates with a spark ignition system and follows a constant volume heat addition process, whereas the Diesel cycle uses compression ignition and follows a constant pressure heat addition process. Diesel engines are generally more efficient because they operate at higher compression ratios, which results in better fuel economy. However, Otto cycle engines are widely used in automobiles due to their lighter weight, faster response, and lower initial costs.

6. Why is the Brayton cycle used in jet engines and gas turbines?
Answer: The Brayton cycle is used in gas turbines and jet engines because it operates with continuous air intake and combustion, making it ideal for high-speed propulsion and power generation. It consists of isentropic compression, constant-pressure heat addition, isentropic expansion, and constant-pressure heat rejection. The ability to sustain high power output with fewer moving parts makes the Brayton cycle highly efficient for aviation and power plants. Additionally, combined cycle gas turbines (CCGTs) integrate the Brayton and Rankine cycles to maximize energy conversion efficiency.

7. How do refrigeration cycles achieve cooling, and what role does the coefficient of performance (COP) play?
Answer: Refrigeration cycles operate by absorbing heat from a low-temperature region and rejecting it to a high-temperature region, typically using a refrigerant as the working fluid. The vapor compression refrigeration cycle, the most common refrigeration cycle, consists of compression, condensation, expansion, and evaporation processes. The efficiency of a refrigeration system is measured by its coefficient of performance (COP), which is defined as COP = Q_C / W, where Q_C is the heat absorbed from the refrigerated space, and W is the work input. Higher COP values indicate more efficient cooling performance.

8. What are the advantages of regenerative and reheat cycles in improving efficiency?
Answer: Regenerative cycles improve efficiency by preheating the feedwater using extracted steam from the turbine, reducing the fuel required to produce steam. This method is widely used in modern Rankine cycle power plants to enhance efficiency and reduce heat losses. Reheat cycles improve efficiency by expanding steam in multiple stages, reheating it between stages to reduce moisture content and increase work output. Both regenerative and reheat cycles increase overall thermal efficiency by reducing irreversibilities and improving energy utilization.

9. How does entropy change in different thermodynamic cycles, and why is it important?
Answer: Entropy change is a measure of irreversibilities in a thermodynamic cycle and plays a crucial role in determining efficiency. In ideal cycles like the Carnot cycle, entropy remains constant during isentropic processes, ensuring maximum theoretical efficiency. However, in real-world cycles, entropy increases due to friction, heat loss, and non-ideal gas behavior, leading to energy dissipation. Engineers analyze entropy generation to identify inefficiencies and develop strategies for energy recovery and optimization, such as using heat exchangers and regenerative systems.

10. What factors influence the efficiency of a thermodynamic cycle, and how can efficiency be improved?
Answer: The efficiency of a thermodynamic cycle depends on temperature limits, pressure ratios, working fluid properties, and system irreversibilities. Higher temperature differences between heat source and sink improve efficiency, as described by the Carnot efficiency equation. Reducing friction, heat loss, and entropy generation also contributes to improved performance. In practical applications, methods such as supercritical operation, multi-stage compression, reheating, regeneration, and better insulation help enhance efficiency and sustainability in power generation, engines, and refrigeration systems.

Thought-Provoking Questions and Answers on Thermodynamics Cycles

1. Why is the Carnot cycle considered an idealized model, and how do real-world cycles differ from it?
Answer: The Carnot cycle is considered an idealized thermodynamic model because it assumes a reversible process with no entropy generation, meaning it operates under perfectly efficient conditions. It consists of two isothermal and two adiabatic processes, ensuring maximum possible efficiency for a heat engine operating between two thermal reservoirs. The efficiency is only dependent on the temperatures of the hot and cold reservoirs, following the equation η = 1 – (T_C / T_H).

In contrast, real-world cycles exhibit irreversibilities due to friction, heat losses, pressure drops, and non-ideal working fluids. These inefficiencies prevent actual systems from reaching the Carnot efficiency. Additionally, practical cycles such as the Rankine, Otto, and Brayton cycles incorporate non-isothermal processes, irreversible expansions and compressions, and real fluid dynamics, which further impact their performance. Despite its limitations, the Carnot cycle serves as a theoretical benchmark for evaluating and improving practical thermodynamic cycles.

2. Why do Rankine cycle power plants often use superheating and reheating, and how do these methods improve efficiency?
Answer: In a Rankine cycle, superheating and reheating are used to increase the thermal efficiency of steam power plants and prevent excessive moisture content in the turbine exhaust. Superheating occurs when steam is heated beyond its saturation temperature, increasing the enthalpy before expansion in the turbine. This process results in higher work output from the steam, reducing energy losses due to condensation.

Reheating is applied in multi-stage turbines, where steam is expanded partially, reheated, and expanded again. This technique reduces moisture formation in later turbine stages, preventing blade erosion and improving longevity. Both superheating and reheating enhance the efficiency of the Rankine cycle by increasing the average temperature of heat addition, thereby bringing the cycle’s performance closer to the ideal Carnot cycle.

3. How do pressure ratios affect the performance of gas turbine cycles, such as the Brayton cycle?
Answer: In the Brayton cycle, commonly used in jet engines and gas turbines, the pressure ratio (the ratio of compressor outlet pressure to inlet pressure) plays a crucial role in determining the thermal efficiency and work output of the system. Higher pressure ratios lead to increased compression efficiency, allowing for greater heat addition in the combustor and higher turbine expansion work.

However, excessive pressure ratios can reduce efficiency due to increased compressor work and higher irreversibilities. Beyond an optimal point, the added work required to compress the air outweighs the benefits of higher thermal efficiency. To optimize performance, modern Brayton cycles use multi-stage compression with intercooling and regeneration, which recycles waste heat to preheat the compressed air, reducing fuel consumption and improving overall efficiency.

4. How does entropy generation affect the efficiency of real thermodynamic cycles?
Answer: Entropy generation represents the irreversibilities present in a thermodynamic system, such as friction, unrestrained expansion, mixing of fluids, and heat transfer across finite temperature differences. The Second Law of Thermodynamics states that entropy in an isolated system always increases, which limits the maximum efficiency of real-world cycles.

As entropy increases, available energy is converted into unusable waste heat, reducing the efficiency of engines, power plants, and refrigeration systems. Engineers use entropy analysis to identify areas of improvement, such as reducing pressure drops, optimizing heat exchangers, and minimizing thermal gradients. Advanced cycles, such as combined-cycle power plants and regenerative heat exchangers, attempt to recover lost energy and improve overall system performance.

5. Why do combined-cycle power plants achieve higher efficiency than single-cycle power plants?
Answer: Combined-cycle power plants achieve higher efficiency by integrating two thermodynamic cycles—typically a gas turbine cycle (Brayton cycle) and a steam turbine cycle (Rankine cycle). In a single-cycle power plant, significant amounts of heat energy are lost in the exhaust gases after expansion in the turbine. However, in a combined-cycle system, this waste heat is captured and used to generate steam, which then drives a steam turbine to produce additional power. By recovering and reusing this energy, combined-cycle plants can achieve efficiencies above 60%, compared to 35–40% in single-cycle plants.

Beyond just efficiency, combined-cycle plants offer advantages in fuel flexibility, reduced emissions, and operational reliability. The sequential use of different cycles allows for better utilization of fuel energy, reducing carbon footprints and minimizing fuel consumption. As energy demands rise and environmental concerns grow, combined-cycle plants are becoming an essential part of modern power generation, especially in reducing reliance on coal-based power plants.

6. How does the Second Law of Thermodynamics place a fundamental limit on the efficiency of thermodynamic cycles?
Answer: The Second Law of Thermodynamics states that entropy always increases in an isolated system, which implies that no energy transformation can be perfectly efficient. In practical terms, this means that a portion of the heat energy supplied to a thermodynamic cycle must be rejected as waste heat to the surroundings. This limitation is evident in the Carnot efficiency equation, which sets the theoretical maximum efficiency of any cycle as:
η = 1 – (T_C / T_H)
where T_C is the temperature of the cold reservoir and T_H is the temperature of the heat source. Since absolute zero (0 K) is unattainable, there is always some amount of heat that must be rejected, making 100% efficiency impossible.

The practical consequence of this limitation is that real-world thermodynamic cycles incorporate additional processes like regeneration, reheat, and intercooling to minimize entropy generation and improve efficiency. Nonetheless, every engine, power plant, or refrigeration system must operate within the constraints of the Second Law, which ensures that some energy will always be lost as unusable heat.

7. Why are supercritical and ultra-supercritical Rankine cycles becoming more popular in modern power generation?
Answer: Supercritical and ultra-supercritical Rankine cycles operate at higher pressures and temperatures than traditional subcritical steam cycles, significantly improving thermal efficiency and reducing fuel consumption. A supercritical Rankine cycle operates at pressures above the critical point of water (22.1 MPa, 374°C), where there is no distinct phase transition between liquid and vapor. This allows for continuous and more efficient heat absorption, reducing energy losses associated with phase change. Ultra-supercritical cycles operate at even higher temperatures (above 600°C), achieving efficiencies over 45%, compared to 35–40% for conventional steam power plants.

The increased efficiency of these advanced Rankine cycles translates into lower CO₂ emissions, reduced fuel costs, and improved sustainability. However, operating at such extreme conditions requires advanced materials, high-strength alloys, and sophisticated cooling techniques to withstand the high temperatures and pressures. Despite the technical challenges, supercritical and ultra-supercritical steam cycles are becoming the industry standard for coal and gas power plants, helping meet global energy demands with lower environmental impact.

8. How does regenerative heat recovery improve the efficiency of thermodynamic cycles?
Answer: Regenerative heat recovery improves the efficiency of thermodynamic cycles by capturing and reusing waste heat from exhaust gases or working fluids. In power generation, this concept is commonly used in Rankine cycles, where extracted steam from a turbine preheats feedwater before it enters the boiler, reducing the energy needed to convert water into steam. This process lowers fuel consumption, improves thermal efficiency, and minimizes entropy generation in the system.

Regeneration is also widely applied in Brayton cycles (gas turbines), where heat exchangers known as regenerators recover heat from exhaust gases and use it to preheat the compressed air before combustion. This increases efficiency by reducing fuel input while maintaining the same work output. Regenerative heat recovery is an essential strategy in sustainable energy systems, waste heat recovery units, and combined heat and power (CHP) plants, helping industries achieve better energy utilization and lower emissions.

9. Why do refrigeration cycles operate in the reverse direction compared to power cycles?
Answer: Refrigeration cycles operate in the reverse direction compared to power cycles because their goal is to remove heat from a low-temperature region and reject it to a higher-temperature region, rather than converting heat into work. In contrast, power cycles extract energy from a high-temperature heat source and convert it into mechanical or electrical energy. Refrigeration cycles require an external work input, usually provided by a compressor, to transfer heat against the natural temperature gradient.

The effectiveness of refrigeration cycles is measured by their coefficient of performance (COP) rather than efficiency. A higher COP indicates a more effective cooling process with less energy input. Refrigeration cycles, such as the vapor compression cycle, are essential in applications like air conditioning, food preservation, cryogenics, and industrial cooling systems. Advanced refrigeration technologies, including absorption refrigeration, magnetic refrigeration, and thermoelectric cooling, continue to improve the efficiency and sustainability of refrigeration processes.

10. How does intercooling improve the efficiency of gas turbine cycles?
Answer: Intercooling is a technique used in gas turbine cycles to increase efficiency and reduce compression work by cooling the working fluid between compression stages. In a simple Brayton cycle, compression raises the temperature of the air, which increases the work required by the compressor. By introducing an intercooler, the compressed air is cooled between compression stages, reducing the required work in the second stage of compression.

Intercooling improves efficiency by reducing the compressor work and increasing the net work output of the cycle. This allows for higher pressure ratios, which enhance the thermal efficiency of the Brayton cycle. Many modern jet engines, gas turbine power plants, and combined-cycle systems incorporate intercooling to optimize performance, reduce specific fuel consumption, and improve operational flexibility.

11. How does the Organic Rankine Cycle (ORC) enhance energy recovery in low-temperature heat sources?
Answer: The Organic Rankine Cycle (ORC) is a variation of the traditional Rankine cycle that uses organic working fluids with lower boiling points than water, making it ideal for extracting energy from low-temperature heat sources such as geothermal, solar thermal, and industrial waste heat recovery. Because these fluids evaporate at lower temperatures, the ORC can operate efficiently where conventional steam Rankine cycles would be ineffective.

By utilizing low-boiling-point working fluids such as R245fa, toluene, or pentane, the ORC maximizes heat recovery from sources typically considered unusable. This allows industries to generate electricity from low-grade heat, improving energy efficiency and reducing environmental impact. ORC technology is widely used in biomass power plants, solar-thermal systems, and heat recovery from internal combustion engines, contributing to sustainable energy solutions.

12. What are the future advancements in thermodynamic cycles for sustainable energy?
Answer: Future advancements in thermodynamic cycles for sustainable energy focus on efficiency improvements, waste heat recovery, and integration with renewable energy sources. Innovations such as supercritical CO₂ cycles, which operate at higher efficiencies and lower environmental footprints than conventional Rankine cycles, are being explored for next-generation power plants. Advanced hydrogen-based cycles, including high-temperature fuel cells and hydrogen combustion cycles, are also gaining traction as potential carbon-free alternatives.

The integration of thermodynamic cycles with renewable energy sources, such as solar-thermal Brayton cycles, geothermal Rankine cycles, and wind-assisted gas turbine systems, is helping to decarbonize power generation. Additionally, closed-loop and regenerative cycles are being optimized for space applications, desalination, and energy storage. As research in thermodynamics, materials science, and energy engineering progresses, the efficiency and sustainability of thermodynamic cycles will continue to evolve, shaping the future of clean energy technologies.

13. What role does exergy analysis play in improving the efficiency of thermodynamic cycles?
Answer: Exergy analysis is a powerful thermodynamic tool that quantifies the maximum useful work that can be extracted from an energy source, taking into account irreversibilities. Unlike energy, which is always conserved (First Law of Thermodynamics), exergy can be destroyed due to entropy generation (Second Law of Thermodynamics). By performing an exergy analysis, engineers can identify where and how energy losses occur in a thermodynamic cycle, leading to more effective system optimizations.

For example, in a Rankine cycle, exergy analysis can reveal that a significant portion of energy is lost during heat transfer in the condenser. To improve efficiency, engineers might implement regenerative feedwater heating to recover some of this lost exergy. Similarly, in gas turbines, exergy destruction due to combustion irreversibility can be minimized by using preheated air or optimized fuel injection techniques. Exergy-based optimization is essential for designing high-efficiency power plants, refrigeration cycles, and sustainable energy systems.

14. How do supercritical CO₂ (sCO₂) power cycles differ from conventional Rankine and Brayton cycles, and what advantages do they offer?
Answer: Supercritical CO₂ power cycles operate at pressures and temperatures where CO₂ exists in a supercritical state, meaning it exhibits properties of both gases and liquids. Unlike traditional steam Rankine cycles, supercritical CO₂ cycles can achieve higher efficiencies (~50%), operate at lower turbine sizes, and require less water, making them attractive for power generation, waste heat recovery, and nuclear applications.

Compared to Brayton cycles, which typically use air as the working fluid, supercritical CO₂ cycles provide higher power density, meaning smaller and more compact turbines can be used. They also have better heat transfer characteristics, allowing for faster response times and improved integration with solar thermal, geothermal, and nuclear power plants. Due to these benefits, sCO₂ power cycles are being actively researched as a next-generation alternative for increasing the sustainability of energy production.

15. How can exergy destruction be minimized in gas turbine cycles to improve efficiency?
Answer: Exergy destruction in gas turbine cycles primarily occurs in combustion, compression, and expansion processes due to irreversibilities such as friction, pressure drops, and non-ideal heat transfer. One way to minimize exergy destruction is by increasing the turbine inlet temperature (TIT) while maintaining material constraints. Higher TIT leads to improved cycle efficiency since the temperature difference between heat input and rejection is maximized, reducing entropy generation.

Another approach is using regenerative heat exchangers, which recover waste heat from the turbine exhaust and use it to preheat the air entering the combustion chamber. This reduces the fuel requirement and increases overall efficiency. Intercooling and reheating can further reduce exergy losses by ensuring that compression and expansion stages occur under more favorable thermodynamic conditions. Advanced solutions, such as ceramic thermal barrier coatings for turbine blades and alternative fuels, are also being explored to minimize exergy destruction in gas turbines.

16. How does the Kalina cycle improve energy efficiency in low-temperature heat recovery applications?
Answer: The Kalina cycle is an advanced thermodynamic cycle that uses a water-ammonia mixture as the working fluid instead of pure water or steam. Unlike the Rankine cycle, where phase change occurs at a constant temperature, the Kalina cycle benefits from a variable boiling and condensation temperature, allowing better heat absorption from low-grade heat sources such as geothermal, industrial waste heat, and solar-thermal power plants.

By exploiting the non-azeotropic behavior of ammonia-water mixtures, the Kalina cycle achieves better thermal matching between the working fluid and heat source, reducing irreversibilities and increasing efficiency. Compared to conventional Rankine cycles, Kalina cycle systems can improve power generation efficiency by 15-30%, making them particularly useful for extracting energy from low-temperature sources where conventional cycles would be ineffective.

17. How do organic Rankine cycles (ORC) enable power generation from low-grade heat sources?
Answer: The Organic Rankine Cycle (ORC) is a modification of the traditional Rankine cycle that uses organic fluids with lower boiling points, such as pentane, toluene, or refrigerants, to generate power from low-grade heat sources like waste heat recovery, geothermal energy, and biomass plants. Unlike water-steam cycles, ORC systems operate at lower temperatures and pressures, making them suitable for heat sources as low as 70–200°C.

The use of low-boiling-point working fluids allows for efficient energy extraction from heat sources where steam-based cycles would be impractical. ORC systems are widely deployed in remote power applications, binary geothermal plants, and industrial waste heat recovery. Advances in supercritical ORC cycles and working fluid optimization continue to improve their feasibility for distributed energy generation and energy efficiency improvements.

18. What is the role of intercooling and reheating in multi-stage compression and expansion cycles?
Answer: Intercooling and reheating are techniques used in multi-stage compression and expansion cycles to enhance efficiency by reducing exergy destruction and work consumption. In compression, intercooling cools the working fluid between compression stages, reducing the required work input. By compressing the gas in stages and removing heat at intermediate points, the cycle reduces entropy generation and enhances thermal performance.

Similarly, in expansion, reheating increases efficiency by adding heat between turbine expansion stages, ensuring a higher temperature gradient for power extraction. This approach prevents excessive moisture formation in steam turbines and increases overall work output. Many advanced power plants, jet engines, and gas turbines employ intercooling and reheating to maximize energy efficiency and improve cycle longevity.

19. How do desalination plants benefit from thermodynamic cycle optimization?
Answer: Desalination plants use multi-stage flash distillation, reverse osmosis, and thermal evaporation to convert seawater into freshwater. Many desalination systems rely on Rankine and Brayton cycle-based energy recovery techniques to reduce power consumption and increase efficiency. Waste heat from power plants is often utilized in thermal desalination units, minimizing exergy losses and improving sustainability.

By optimizing thermodynamic cycles, engineers can develop hybrid desalination systems that integrate low-grade heat recovery, cogeneration, and renewable energy sources. Technologies like low-temperature organic Rankine cycles (LT-ORC) and solar-thermal desalination are being actively developed to enhance energy efficiency and reduce the environmental impact of water purification.

20. What future advancements in thermodynamic cycles could revolutionize power generation and sustainability?
Answer: Future advancements in thermodynamic cycles aim to enhance energy efficiency, reduce environmental impact, and integrate with sustainable energy systems. One promising area of research is hydrogen-based thermodynamic cycles, where hydrogen combustion or fuel cells could provide zero-carbon power generation with high efficiency. Supercritical CO₂ cycles, with their high power density and reduced water usage, are also expected to play a major role in the next generation of power plants.

Other innovations include waste heat-to-power technologies, where thermoelectric and thermophotovoltaic systems convert heat directly into electricity without moving parts, reducing maintenance costs. Additionally, energy storage technologies, such as compressed air energy storage (CAES) and pumped thermal energy storage (PTES), are being developed to complement renewable energy sources by improving grid stability and energy dispatchability. These advancements will help create a more sustainable, low-carbon energy future driven by optimized thermodynamic cycles.

Numerical Problems and Solutions on Thermodynamics Cycles

1. A Carnot engine operates between a high-temperature reservoir at 800 K and a low-temperature reservoir at 300 K. Calculate its efficiency.
Solution:

  • Given: T_H = 800 K, T_C = 300 K
  • Efficiency formula: η = 1 – (T_C / T_H)
  • Substituting values:
    η = 1 – (300 / 800) = 1 – 0.375 = 0.625
  • Final Answer: 62.5% efficiency

2. A Rankine cycle operates with steam entering the turbine at 3 MPa and 600°C, and the condenser pressure is 10 kPa. Determine the thermal efficiency assuming an ideal cycle.
Solution:

  • Use steam tables to determine enthalpies at different points.
  • Find enthalpy at turbine inlet: h1 = 3650 kJ/kg
  • Find enthalpy at turbine outlet (isentropic expansion): h2 = 1800 kJ/kg
  • Find enthalpy at condenser outlet: h3 = 500 kJ/kg
  • Find enthalpy at pump exit: h4 = 505 kJ/kg
  • Work output of turbine: W_t = h1 – h2 = 3650 – 1800 = 1850 kJ/kg
  • Work input to pump: W_p = h4 – h3 = 505 – 500 = 5 kJ/kg
  • Net work done: W_net = W_t – W_p = 1850 – 5 = 1845 kJ/kg
  • Heat input: Q_in = h1 – h4 = 3650 – 505 = 3145 kJ/kg
  • Efficiency formula: η = W_net / Q_in
    η = 1845 / 3145 = 0.587
  • Final Answer: 58.7% efficiency

3. A gas turbine in a Brayton cycle operates with an inlet pressure of 100 kPa and an outlet pressure of 1000 kPa. The air enters the compressor at 300 K and the turbine at 1200 K. Determine the thermal efficiency assuming an ideal cycle (γ = 1.4).

Solution:

  • Given: P1 = 100 kPa, P2 = 1000 kPa, T1 = 300 K, T3 = 1200 K, γ = 1.4
  • Efficiency formula for an ideal Brayton cycle:
    η = 1 – (T1 / T3) [(P1 / P2)^( (γ-1)/γ )]
  • Substituting values:
    η = 1 – (300 / 1200) [(100 / 1000)^((1.4-1)/1.4)]
    η = 1 – (0.25) [(0.1)^(0.4/1.4)]
    η = 1 – (0.25) (0.398)
    η = 1 – 0.0995
    η = 0.9005
  • Final Answer: 90.05% efficiency

4. A heat pump using the vapor compression cycle extracts 25 kW of heat from a low-temperature reservoir and delivers 60 kW to a high-temperature reservoir. Determine the coefficient of performance (COP).

Solution:

  • Given: Q_C = 25 kW, Q_H = 60 kW
  • Work input: W = Q_H – Q_C = 60 – 25 = 35 kW
  • COP formula: COP_HP = Q_H / W
    COP_HP = 60 / 35
    COP_HP = 1.71
  • Final Answer: 1.71

5. A Carnot refrigerator operates between 260 K (cold reservoir) and 320 K (hot reservoir). Calculate its coefficient of performance (COP).

Solution:

  • Given: T_C = 260 K, T_H = 320 K
  • COP formula for a Carnot refrigerator:
    COP = T_C / (T_H – T_C)
    COP = 260 / (320 – 260)
    COP = 260 / 60
    COP = 4.33
  • Final Answer: 4.33

6. In a Rankine cycle, steam enters the turbine at 4 MPa and 600°C and is condensed at 10 kPa. The mass flow rate is 5 kg/s. Determine the turbine power output assuming an ideal cycle.

Solution:

  • Use steam tables to determine enthalpies:
    • h1 (steam inlet) = 3650 kJ/kg
    • h2 (steam outlet) = 2000 kJ/kg
  • Work done per kg:
    W_t = h1 – h2 = 3650 – 2000 = 1650 kJ/kg
  • Power output:
    P = m × W_t = 5 × 1650
    P = 8250 kW
  • Final Answer: 8250 kW turbine power output

7. A Diesel engine operates with a compression ratio of 20. The temperature before compression is 300 K. If the heat addition occurs at constant pressure, determine the temperature at the end of compression assuming an ideal Diesel cycle (γ = 1.4).

Solution:

  • Given: r = 20, T1 = 300 K, γ = 1.4
  • Compression temperature formula:
    T2 = T1 × r^(γ-1)
    T2 = 300 × 20^(1.4-1)
    T2 = 300 × 20^0.4
    T2 = 300 × 2.639
    T2 = 791.7 K
  • Final Answer: 791.7 K

8. A simple Rankine cycle operates with steam entering the turbine at 6 MPa and 600°C and leaving at 10 kPa. The pump requires 15 kJ/kg of work. Find the thermal efficiency assuming an ideal cycle.

Solution:

  • Use steam tables to determine enthalpies:
    • h1 = 3650 kJ/kg
    • h2 = 2000 kJ/kg
    • h3 = 500 kJ/kg
    • h4 = 505 kJ/kg
  • Work output:
    W_t = h1 – h2 = 3650 – 2000 = 1650 kJ/kg
  • Work input:
    W_p = h4 – h3 = 505 – 500 = 5 kJ/kg
  • Net work:
    W_net = W_t – W_p = 1650 – 5 = 1645 kJ/kg
  • Heat input:
    Q_in = h1 – h4 = 3650 – 505 = 3145 kJ/kg
  • Efficiency formula:
    η = W_net / Q_in
    η = 1645 / 3145
    η = 0.523
  • Final Answer: 52.3% efficiency
 

13. A reheat Rankine cycle operates with steam entering the high-pressure turbine at 10 MPa and 600°C and is reheated at 4 MPa to 600°C before entering the low-pressure turbine. The condenser pressure is 10 kPa. Determine the thermal efficiency of the cycle.

Solution:

  • Given:
    • P1 = 10 MPa, T1 = 600°C (high-pressure turbine inlet)
    • P2 = 4 MPa, T2 = 600°C (after reheating)
    • P3 = 10 kPa (condenser pressure)

  1. Obtain enthalpies from steam tables:

    • h1 = 3650 kJ/kg (before expansion in the high-pressure turbine)
    • h2 = 2800 kJ/kg (after expansion to 4 MPa)
    • h3 = 3650 kJ/kg (after reheating to 600°C)
    • h4 = 2100 kJ/kg (after expansion in the low-pressure turbine)
    • h5 = 500 kJ/kg (after condensation)

  2. Work done by turbines:

    • High-pressure turbine: W_HP = h1 – h2 = 3650 – 2800 = 850 kJ/kg
    • Low-pressure turbine: W_LP = h3 – h4 = 3650 – 2100 = 1550 kJ/kg
    • Total work output: W_net = W_HP + W_LP = 850 + 1550 = 2400 kJ/kg

  3. Heat input in the boiler and reheater:

    • Q_in = (h1 – h5) + (h3 – h2)
    • Q_in = (3650 – 500) + (3650 – 2800)
    • Q_in = 3150 + 850 = 4000 kJ/kg

  4. Thermal efficiency calculation:

    • η = W_net / Q_in = 2400 / 4000
    • η = 0.6 or 60%
  • Final Answer: 60% efficiency

14. A gas turbine power plant with a regenerator operates between pressure limits of 100 kPa and 1000 kPa. The temperature before entering the turbine is 1100 K, and after expansion, it drops to 700 K. The regenerator effectiveness is 80%. Calculate the thermal efficiency.

Solution:

  • Given:
    • P1 = 100 kPa, P2 = 1000 kPa
    • T1 = 300 K, T3 = 1100 K, T4 = 700 K
    • Effectiveness = 80%

  1. Determine the ideal temperature after compression using isentropic relations:

    • T2 = T1 × (P2/P1)^( (γ-1)/γ )
    • T2 = 300 × (1000/100)^( (1.4-1)/1.4 )
    • T2 = 300 × (10)^0.2857
    • T2 = 300 × 1.86 = 558 K

  2. Regenerator exit temperature (T5) using effectiveness formula:

    • T5 = T2 + Effectiveness × (T4 – T2)
    • T5 = 558 + 0.8 × (700 – 558)
    • T5 = 558 + 0.8 × 142
    • T5 = 558 + 113.6 = 671.6 K

  3. Determine work output and heat input:

    • W_turbine = Cp × (T3 – T4) = (1.005 kJ/kg·K) × (1100 – 700)
    • W_turbine = 1.005 × 400 = 402 kJ/kg
    • W_compressor = Cp × (T2 – T1) = (1.005 kJ/kg·K) × (558 – 300)
    • W_compressor = 1.005 × 258 = 259 kJ/kg
    • Net work output: W_net = W_turbine – W_compressor = 402 – 259 = 143 kJ/kg
    • Heat input from regenerator:
      • Q_in = Cp × (T3 – T5) = 1.005 × (1100 – 671.6)
      • Q_in = 1.005 × 428.4 = 430.5 kJ/kg

  4. Thermal efficiency:

    • η = W_net / Q_in = 143 / 430.5
    • η = 0.332 or 33.2%
  • Final Answer: 33.2% efficiency

15. A combined-cycle power plant consists of a gas turbine and a steam Rankine cycle. The gas turbine has an efficiency of 40%, and the Rankine cycle has an efficiency of 35%. The gas turbine produces 100 MW of power. Determine the total power output and overall efficiency of the plant.

Solution:

  1. Power output of Rankine cycle:

    • Power input to Rankine cycle = (1 – η_GT) × Power_GT
    • = (1 – 0.4) × 100 MW
    • = 0.6 × 100 MW = 60 MW

  2. Power produced by Rankine cycle:

    • Power_Rankine = η_Rankine × 60 MW
    • = 0.35 × 60 MW = 21 MW

  3. Total power output:

    • Power_total = Power_GT + Power_Rankine
    • = 100 MW + 21 MW
    • = 121 MW

  4. Overall efficiency of the combined cycle:

    • η_total = Power_total / (Fuel Input to GT)
    • Fuel input to GT = Power_GT / η_GT = 100 / 0.4 = 250 MW
    • η_total = 121 / 250 = 0.484 or 48.4%
  • Final Answers: Total power output = 121 MW, Overall efficiency = 48.4%

16. A gas turbine operating on the Brayton cycle has a compressor with a pressure ratio of 8. The temperature at the inlet of the compressor is 300 K, and the maximum temperature in the cycle is 1400 K. Assuming an ideal cycle and γ = 1.4, calculate the thermal efficiency.

Solution:

  • Given: P2/P1 = 8, T1 = 300 K, T3 = 1400 K, γ = 1.4
  • Thermal efficiency for an ideal Brayton cycle:
    η = 1 – (T1 / T3) × (P1/P2)^( (γ-1)/γ )
  • Substituting values:
    η = 1 – (300/1400) × (1/8)^( (1.4-1)/1.4 )
    η = 1 – (0.214) × (0.297)
    η = 1 – 0.0636
    η = 0.9364 or 93.64%
  • Final Answer: 93.64% efficiency

17. A refrigeration system using a vapor compression cycle absorbs 45 kW of heat from a refrigerated space. If the system has a coefficient of performance (COP) of 3.8, determine the required work input.

Solution:

  • Given: Q_C = 45 kW, COP = 3.8
  • COP formula for a refrigerator:
    COP = Q_C / W
  • Solving for work input:
    W = Q_C / COP
    W = 45 / 3.8
    W = 11.84 kW
  • Final Answer: 11.84 kW work input

18. A Diesel engine operates with a compression ratio of 18. The temperature before compression is 320 K, and the pressure before compression is 100 kPa. Calculate the temperature and pressure at the end of compression assuming an ideal cycle with γ = 1.4.

Solution:

  • Given: r = 18, T1 = 320 K, P1 = 100 kPa, γ = 1.4
  • Temperature after compression:
    T2 = T1 × r^(γ-1)
    T2 = 320 × 18^(0.4)
    T2 = 320 × 2.798
    T2 = 895.4 K
  • Pressure after compression:
    P2 = P1 × r^γ
    P2 = 100 × 18^(1.4)
    P2 = 100 × 45.75
    P2 = 4575 kPa
  • Final Answers: T2 = 895.4 K, P2 = 4575 kPa

19. A Carnot heat engine operates between a high-temperature reservoir at 1000 K and a low-temperature reservoir at 300 K. If the engine receives 500 kJ of heat, determine the work output and the heat rejected.

Solution:

  • Given: T_H = 1000 K, T_C = 300 K, Q_in = 500 kJ
  • Carnot efficiency:
    η = 1 – (T_C / T_H)
    η = 1 – (300 / 1000)
    η = 1 – 0.3 = 0.7
  • Work output:
    W = η × Q_in
    W = 0.7 × 500
    W = 350 kJ
  • Heat rejected:
    Q_out = Q_in – W
    Q_out = 500 – 350
    Q_out = 150 kJ
  • Final Answers: W = 350 kJ, Q_out = 150 kJ