Prepare for University Studies & Career Advancement

Engineering Thermodynamics

Engineering Thermodynamics

Engineering thermodynamics is a foundational discipline that underpins much of mechanical, chemical, and aerospace engineering. It explores how energy is transformed between heat and work, and how these transformations govern the performance of engines, power plants, refrigeration cycles, and more. Unlike pure theoretical studies, engineering thermodynamics emphasizes practical applications grounded in the core principles of thermodynamics, especially as framed by the laws of thermodynamics, which establish constraints for all energy-conversion processes.

A solid understanding of classical thermodynamics is essential for analyzing systems like internal combustion engines and gas turbines. These systems often operate within well-defined thermodynamic cycles, such as the Otto and Rankine cycles, where pressure, volume, and temperature interact in predictable patterns. Further, heat transfer mechanisms—conduction, convection, and radiation—are central to optimizing thermal efficiency and avoiding material degradation.

The growing demand for cleaner technologies has also led engineers to explore renewable and sustainable energy thermodynamics. Solar thermal systems, biomass combustion, and geothermal energy all require a deep thermodynamic analysis to assess feasibility and efficiency. These efforts are increasingly supported by computational thermodynamics, which allows for high-precision modeling of complex systems that would be analytically intractable.

To better handle systems outside of equilibrium—such as combustion processes and transient heat flow—students are introduced to non-equilibrium thermodynamics. In advanced cases, these principles are further complemented by statistical thermodynamics, which links macroscopic properties to microscopic particle behavior. Understanding phase equilibria and chemical potentials is especially useful in systems involving fuels, refrigerants, or multi-phase mixtures.

The practical applications of engineering thermodynamics stretch beyond engines and into materials design, through studies like thermodynamics of materials. Engineers must understand how temperature affects strength, ductility, and failure modes in structural components. These insights often intersect with electrodynamics and plasma physics in energy and aerospace applications.

A deeper understanding of thermodynamics also enhances comprehension of modern physics topics such as modern physics, relativity, and quantum mechanics. At the atomic level, energy states and heat capacities depend on principles introduced in atomic physics, while high-temperature systems may involve nuclear reactions or even nuclear fusion. Students are thus encouraged to develop an interdisciplinary approach, linking physics and science fundamentals with applications in physical chemistry and beyond.

Engineering thermodynamics not only equips students with tools to solve real-world energy challenges, but also cultivates a systems-thinking mindset crucial for innovation. It provides the thermodynamic literacy required to model, analyze, and optimize energy systems across industries—from automotive and aerospace to sustainable infrastructure and power generation.

Engineering Thermodynamics, showcasing energy transfer in internal combustion engines, power plants, and refrigeration systems, with glowing heat flows and thermodynamic cycle representations.
Engineering Thermodynamics: showcasing energy transfer in internal combustion engines, power plants, and refrigeration systems, with glowing heat flows and thermodynamic cycle representations.
This visually rich illustration represents the core concepts of engineering thermodynamics. At the center is a detailed internal combustion engine surrounded by glowing arcs of heat and energy, symbolizing dynamic thermal processes such as heat input, work output, and entropy flow. The surrounding graphics depict data charts, pressure–volume diagrams, and entropy plots—representing thermodynamic cycles used in engines, power generation, and refrigeration systems. The image integrates vibrant color-coded flows to highlight the movement of energy and transformations of state, making abstract concepts like the Carnot, Otto, or Rankine cycles visually intuitive. This artwork serves as an engaging educational metaphor for the study of energy systems and thermodynamic principles in mechanical and energy engineering.

Table of Contents

Basic Concepts in Engineering Thermodynamics

System and Surroundings

  • System: The part of the universe chosen for analysis (e.g., steam in a boiler).
  • Surroundings: Everything outside the system that interacts with it.
  • Boundary: The interface between the system and its surroundings.

Types of Systems

  • Open System (Control Volume): Exchanges both matter and energy with its surroundings (e.g., turbines, compressors).
  • Closed System: Exchanges energy but not matter (e.g., gas in a piston-cylinder).
  • Isolated System: No exchange of energy or matter (idealized concept).

Properties of Systems

  • Intensive Properties: Independent of system size (e.g., temperature, pressure).
  • Extensive Properties: Depend on system size (e.g., mass, volume).
  • State: The condition of a system described by its properties.
  • Process: The transition of a system from one state to another.
  • Cycle: A series of processes returning the system to its initial state.

Fundamental Laws of Thermodynamics

Zeroth Law of Thermodynamics

Statement:
If two systems are each in thermal equilibrium with a third system, they are in thermal equilibrium with each other.

Implication:
Establishes the concept of temperature and forms the basis for temperature measurement.

First Law of Thermodynamics (Law of Energy Conservation)

Statement:
Energy cannot be created or destroyed; it can only change forms. The total energy of an isolated system is constant.

Mathematical Form:

ΔU=Q−W\Delta U = Q – W

Where:

ΔU = Change in internal energy.

Q = Heat added to the system.

W = Work done by the system  

Implication:

This law is used to analyze energy balance in systems like engines, boilers, and heat exchangers.

Second Law of Thermodynamics

Statement:
In any natural thermodynamic process, the total entropy of a system and its surroundings always increases.

ΔSuniverse=ΔSsystem+ΔSsurroundings≥0\Delta S_{\text{universe}} = \Delta S_{\text{system}} + \Delta S_{\text{surroundings}} \geq 0

Implications:

  • Introduces the concept of entropy (measure of disorder).
  • Explains why heat flows from hot to cold.
  • Sets limits on the efficiency of energy conversion devices.

4. Third Law of Thermodynamics

Statement:
As a system approaches absolute zero temperature, its entropy approaches zero.

lim⁡T→0S=0\lim_{T \to 0} S = 0

Implication:
It is impossible to reach absolute zero temperature, as doing so would require infinite energy.

Forms of Energy in Engineering Systems

  1. Internal Energy (U): Energy related to molecular motion and interactions.
  2. Kinetic Energy (KE): Energy due to system motion.
  3. Potential Energy (PE): Energy due to system position.
  4. Thermal Energy: Energy related to the temperature of a substance.
  5. Mechanical Energy: Sum of kinetic and potential energy, often used for performing work.

Modes of Heat and Work Transfer

Heat Transfer

  • Conduction: Transfer of heat through solids.
  • Convection: Transfer of heat through fluids.
  • Radiation: Transfer of heat through electromagnetic waves.

Work Transfer

  • Boundary Work: Due to volume changes in the system.
  • Shaft Work: Due to rotating shafts in engines.
  • Electrical Work: Due to electrical currents.

Thermodynamic Processes

  1. Isothermal Process: Constant temperature (ΔT = 0)
  2. Adiabatic Process: No heat exchange (Q = 0)
  3. Isobaric Process: Constant pressure (ΔP = 0)
  4. Isochoric Process: Constant volume (ΔV = 0)
  5. Polytropic Process: A general process described by
    PVn=constantPV^n = \text{constant}

     

     

Thermodynamic Cycles

Carnot Cycle

  • Idealized cycle representing the maximum possible efficiency.
  • Involves reversible isothermal and adiabatic processes.

Otto Cycle

  • Models spark-ignition engines (e.g., gasoline engines).
  • Involves adiabatic compression and expansion with constant volume heat addition.
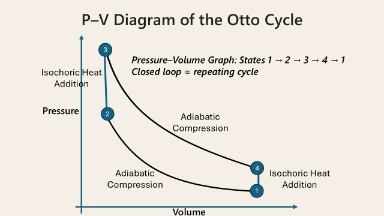
P–V diagram showing the four thermodynamic processes of the Otto Cycle: adiabatic compression (1→2), isochoric heat addition (2→3), adiabatic expansion (3→4), and isochoric heat rejection (4→1), forming a closed loop.
P–V Diagram of the Otto Cycle The pressure–volume graph illustrates a complete thermodynamic cycle used in petrol engines. The loop follows the sequence 1 → 2 → 3 → 4 → 1, representing compression, combustion, expansion, and exhaust.

This pressure–volume (P–V) diagram illustrates the Otto Cycle, the fundamental thermodynamic process behind spark-ignition internal combustion engines. The cycle comprises four stages: adiabatic compression from point 1 to 2, isochoric heat addition from 2 to 3, adiabatic expansion from 3 to 4, and isochoric heat rejection from 4 back to 1. The closed loop on the graph signifies a repeating cycle, where the gas in the engine cylinder undergoes cyclic transformations of pressure and volume, ultimately converting thermal energy into mechanical work.

Diesel Cycle

  • Models compression-ignition engines (e.g., diesel engines).
  • Involves constant pressure heat addition.
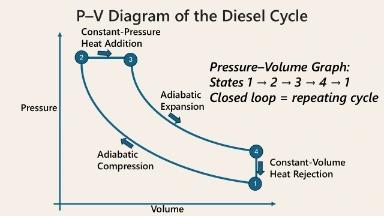
Pressure-Volume Diagram of Diesel Cycle
P–V Diagram of the Diesel Cycle This pressure–volume diagram illustrates the four stages of the Diesel Cycle: compression, combustion, expansion, and exhaust. The graph follows the path 1 → 2 → 3 → 4 → 1, showing how pressure and volume change during each thermodynamic process.

The Diesel Cycle P–V diagram represents the thermodynamic cycle used in compression-ignition engines, such as those in diesel vehicles. It consists of four key processes: adiabatic compression from point 1 to 2, constant-pressure heat addition from 2 to 3, adiabatic expansion from 3 to 4, and constant-volume heat rejection from 4 back to 1. Unlike the Otto Cycle, the Diesel Cycle involves heat addition at constant pressure, reflecting the combustion characteristics of diesel engines. The enclosed loop demonstrates the repeating nature of the cycle, where thermal energy is converted into mechanical work through cyclic pressure–volume transformations.

Rankine Cycle

  • Used in steam power plants.
  • Converts heat energy to mechanical work using steam.

Brayton Cycle

  • Used in gas turbines and jet engines.
  • Involves isentropic compression and expansion with constant pressure heat addition.

Applications of Engineering Thermodynamics

Power Generation

  • Thermal power plants use the Rankine cycle to convert fuel energy into electricity.
  • Nuclear power plants apply thermodynamic principles for safe energy generation.

Internal Combustion Engines

  • Otto and Diesel cycles explain the working of gasoline and diesel engines.
  • Thermodynamics aids in improving fuel efficiency and reducing emissions.

Refrigeration and Air Conditioning

  • Based on the reversed Carnot and vapor-compression cycles.
  • Used in household refrigerators, air conditioners, and industrial cooling systems.

Aerospace Engineering

Renewable Energy Systems

  • Thermodynamics optimizes solar thermal, wind, and geothermal energy systems.
  • Helps improve efficiency and sustainability.

Chemical Process Industries

  • Design and operation of reactors, distillation columns, and heat exchangers rely on thermodynamic principles.
  • Used for energy optimization and waste reduction.

Emerging Trends in Engineering Thermodynamics

Sustainable Energy Solutions

  • Focus on improving renewable energy systems (solar, wind, biofuels).
  • Development of energy storage systems.

Waste Heat Recovery

  • Capturing waste heat to improve system efficiency.
  • Applications in industrial processes and automotive systems.

Advanced Materials

  • Development of thermal barrier coatings and phase-change materials.
  • Enhances efficiency and durability of engineering systems.

Nano-Scale Thermodynamics

  • Applying thermodynamic principles at the nanoscale for microelectronics and nanotechnology.
  • Essential for designing MEMS and NEMS devices.

Why Study Engineering Thermodynamics

Practical Application of Thermodynamic Principles

Engineering thermodynamics focuses on applying thermodynamic laws to machines and systems. Students learn to analyze engines, turbines, heat exchangers, and refrigeration units. It emphasizes the conversion of energy into useful work. It is fundamental for mechanical, aerospace, and chemical engineering disciplines.

Cycle Analysis and System Efficiency

Students study ideal and real cycles like the Rankine, Brayton, and vapor-compression cycles. These help evaluate the performance of thermal systems. Understanding cycle analysis is key to optimizing design and reducing losses. It enhances engineering decision-making and innovation.

Energy Conservation and Sustainability

Engineering thermodynamics equips students to assess energy usage and efficiency. They explore how to minimize waste, recover energy, and design sustainable processes. These skills are vital for addressing global energy challenges. They promote environmentally responsible engineering practices.

Real Substances and Non-Ideal Behavior

Students use real gas models, property tables, and equations of state for practical systems. These allow accurate analysis beyond ideal assumptions. They help bridge classroom learning with real-world complexity. They prepare students for robust and reliable engineering design.

Essential for Industry and Innovation

Knowledge of engineering thermodynamics is essential for careers in power generation, manufacturing, and HVAC systems. It supports the development of advanced engines, sustainable technologies, and thermal devices. It prepares students for both industrial roles and graduate research. It builds a foundation for impactful engineering work.

 

Engineering Thermodynamics: Conceptual Questions and Answers

Question 1:

Why can’t a heat engine be 100% efficient according to the Second Law of Thermodynamics?

Answer:
The Second Law of Thermodynamics states that no heat engine can convert all the absorbed heat into work because some energy must always be rejected to a cold reservoir. This is due to the natural tendency of energy to disperse, increasing the system’s entropy. Thus, achieving 100% efficiency is impossible.

Question 2:

What is the difference between an open system and a closed system in thermodynamics?

Answer:

  • An open system can exchange both matter and energy with its surroundings (e.g., turbines, pumps).
  • A closed system can exchange only energy but not matter (e.g., a gas in a piston-cylinder).
  • An isolated system exchanges neither energy nor matter.

Question 3:

Why is the Carnot cycle considered the most efficient cycle?

Answer:
The Carnot cycle is composed of reversible processes (two isothermal and two adiabatic), ensuring maximum possible efficiency between two thermal reservoirs. Its efficiency depends only on the temperatures of the hot and cold reservoirs:

ηCarnot=1−TCTH\eta_{\text{Carnot}} = 1 – \frac{T_C}{T_H}

No real engine can exceed the Carnot efficiency.

Question 4:

What is the significance of entropy in thermodynamics?

Answer:
Entropy is a measure of disorder in a system. The Second Law of Thermodynamics states that in any spontaneous process, the total entropy of the universe always increases. It defines the direction of natural processes and limits energy conversions.

Question 5:

What is the difference between heat and work in thermodynamics?

Answer:

  • Heat (Q): Energy transferred due to a temperature difference between a system and its surroundings.
  • Work (W): Energy transferred when a force moves an object or when a system boundary moves.

Both heat and work are forms of energy transfer but differ in their mechanisms.

Question 6:

How does increasing the compression ratio affect the efficiency of an Otto cycle?

Answer:
The efficiency of the Otto cycle increases with a higher compression ratio because the air-fuel mixture is compressed more, leading to greater energy release during combustion. However, excessively high compression ratios may cause engine knocking.

Question 7:

Why is the Rankine cycle preferred in steam power plants over the Carnot cycle?

Answer:
The Rankine cycle is more practical than the Carnot cycle because it handles phase changes between liquid and vapor more efficiently. The Carnot cycle requires isothermal heat transfer during vaporization, which is difficult to achieve practically.

Question 8:

What is the purpose of regeneration in thermodynamic cycles?

Answer:
Regeneration improves cycle efficiency by using steam extracted from the turbine to preheat the feedwater before it enters the boiler. This reduces the fuel required to heat the water, increasing the Rankine cycle efficiency.

Engineering Thermodynamics: Numerical Examples with Solutions

Example 1: First Law of Thermodynamics

Problem:
A system absorbs 800 J of heat and does 300 J of work. Find the change in internal energy.

Solution:

ΔU=Q−W=800−300=500 J\Delta U = Q – W = 800 – 300 = 500 \, \text{J}

Answer:
The change in internal energy is 500 J.

Example 2: Carnot Efficiency

Problem:
A Carnot engine operates between a hot reservoir at 600 K and a cold reservoir at 300 K. Find its efficiency.

Solution:

η=1−TCTH=1−300600=0.5\eta = 1 – \frac{T_C}{T_H} = 1 – \frac{300}{600} = 0.5

Answer:
The efficiency is 50%.

Example 3: Work Done in Isothermal Expansion

Problem:
Calculate the work done by 1 mole of an ideal gas expanding isothermally from 1 L to 5 L at 300 K.

Solution:

W=nRTln⁡(VfVi)=1×8.314×300ln⁡(51)W = nRT \ln\left(\frac{V_f}{V_i}\right) = 1 \times 8.314 \times 300 \ln\left(\frac{5}{1}\right)

W=2494.2×1.6094≈4014.59 JW = 2494.2 \times 1.6094 \approx 4014.59 \, \text{J}

Answer:
The work done is 4014.59 J.

Example 4: Heat Rejected by a Carnot Engine

Problem:
A Carnot engine absorbs 1000 J from a hot reservoir at 500 K and operates between 500 K and 300 K. How much heat is rejected?

Solution:

η=1−TCTH=1−300500=0.4\eta = 1 – \frac{T_C}{T_H} = 1 – \frac{300}{500} = 0.4

W=η×Qin=0.4×1000=400 JW = \eta \times Q_{\text{in}} = 0.4 \times 1000 = 400 \, \text{J}

Qout=Qin−W=1000−400=600 JQ_{\text{out}} = Q_{\text{in}} – W = 1000 – 400 = 600 \, \text{J}

Answer:
The heat rejected is 600 J.

Example 5: Entropy Change

Problem:
Calculate the entropy change when 500 J of heat is transferred to a system at 350 K.

Solution:

ΔS=QT=500350≈1.43 J/K\Delta S = \frac{Q}{T} = \frac{500}{350} \approx 1.43 \, \text{J/K}

Answer:
The entropy change is 1.43 J/K.

Example 6: Otto Cycle Efficiency

Problem:
An Otto engine has a compression ratio of 10. Find its efficiency assuming

γ=1.4\gamma = 1.4

Solution:

η=1−1rγ−1=1−1100.4≈1−0.398=0.602\eta = 1 – \frac{1}{r^{\gamma – 1}} = 1 – \frac{1}{10^{0.4}} \approx 1 – 0.398 = 0.602

Answer:
The efficiency is 60.2%.

Example 7: Rankine Cycle Efficiency

Problem:
A steam power plant operating on the Rankine cycle receives 2500 kJ/kg of heat and rejects 1500 kJ/kg. Find its efficiency.

Solution:

η=Qin−QoutQin=2500−15002500=0.4\eta = \frac{Q_{\text{in}} – Q_{\text{out}}}{Q_{\text{in}}} = \frac{2500 – 1500}{2500} = 0.4

Answer:
The efficiency is 40%.

Example 8: Heat Required to Melt Ice

Problem:
How much heat is required to melt 2 kg of ice at 0°C? (Latent heat of fusion of ice = 334 kJ/kg)

Solution:

Q=m×Lf=2×334=668 kJQ = m \times L_f = 2 \times 334 = 668 \, \text{kJ}

Answer:
The heat required is 668 kJ.

Engineering Thermodynamics: Conclusion

Engineering Thermodynamics is a foundational subject that applies the principles of energy conversion and heat transfer to solve real-world engineering problems. By understanding the laws of thermodynamics, engineers design efficient and sustainable systems for power generation, transportation, refrigeration, and manufacturing.

The ongoing focus on renewable energy, sustainability, and efficiency improvements ensures that engineering thermodynamics will continue to be a critical field in advancing technology and solving global energy challenges.

Engineering Thermodynamics: Review Questions and Answers:

1. What is engineering thermodynamics?
Answer: Engineering thermodynamics applies the fundamental laws of thermodynamics to design and analyze energy systems. It focuses on converting energy forms, optimizing efficiency, and solving practical engineering problems.

2. What are the main laws of thermodynamics used in engineering?
Answer: The main laws include the First Law (energy conservation), the Second Law (entropy increase and irreversibility), and the Third Law (behavior near absolute zero), which together govern energy exchange and efficiency in systems.

3. How does the First Law of Thermodynamics apply to energy systems?
Answer: The First Law states that energy cannot be created or destroyed, only transformed. In engineering, it ensures that the total energy input into a system equals the sum of the work output and the change in internal energy, crucial for energy balance in machines.

4. What is the significance of the Second Law in engineering thermodynamics?
Answer: The Second Law introduces the concept of entropy, dictating that energy transformations are never 100% efficient. It sets limits on the maximum efficiency of engines and refrigerators, guiding the design of practical systems.

5. How do closed and open systems differ in thermodynamics?
Answer: A closed system exchanges energy but not mass with its surroundings, while an open system exchanges both energy and mass. This distinction affects the analysis and design of processes like combustion or refrigeration.

6. What is a thermodynamic cycle, and why is it important in engineering?
Answer: A thermodynamic cycle is a series of processes that return a system to its initial state. It is used in engines and refrigerators to convert heat into work or vice versa, and its efficiency determines the performance of the system.

7. How does the Carnot cycle help in understanding engine efficiency?
Answer: The Carnot cycle is an idealized reversible cycle that establishes the maximum possible efficiency for a heat engine operating between two temperatures. It serves as a benchmark for evaluating real engine performance.

8. What role do heat exchangers play in engineering thermodynamics?
Answer: Heat exchangers transfer thermal energy between fluids without mixing them. They are essential components in power plants, refrigeration, and HVAC systems, improving energy efficiency and process control.

9. How is the concept of exergy used in engineering thermodynamics?
Answer: Exergy measures the useful work potential of a system relative to its environment. It helps identify inefficiencies and losses in energy systems, guiding improvements in design and operation.

10. What are some common applications of engineering thermodynamics in industry?
Answer: Applications include power generation, refrigeration, air conditioning, automotive engines, and chemical process design. These applications rely on thermodynamic principles to optimize energy use and system efficiency.

 

Engineering Thermodynamics: Thought-Provoking Questions and Answers

1. How could advances in engineering thermodynamics drive the development of more sustainable energy systems?
Answer: A deeper understanding of energy conversion and efficiency can lead to the design of advanced cycles and heat management strategies that minimize waste and maximize output. Innovations like supercritical CO₂ cycles or enhanced waste heat recovery could dramatically reduce emissions and improve renewable energy systems.

2. In what ways can integrating exergy analysis with traditional thermodynamic methods improve industrial process design?
Answer: Exergy analysis identifies where energy degradation occurs, pinpointing inefficiencies in a system. When combined with conventional thermodynamics, it enables engineers to design processes that not only conserve energy but also make optimal use of the available energy, leading to more efficient and sustainable operations.

3. How might the principles of thermodynamics inform the future design of high-efficiency vehicles?
Answer: By applying thermodynamic optimization to engine cycles, waste heat recovery, and advanced materials, engineers can develop vehicles with improved fuel economy and reduced emissions. This includes hybrid systems and alternative fuel engines that better harness and convert energy.

4. What role does computational thermodynamics play in modern engineering, and how can it transform process optimization?
Answer: Computational thermodynamics uses simulations and numerical methods to predict system behavior under various conditions. This allows for rapid prototyping, optimization of industrial processes, and the design of systems with enhanced performance, all while reducing experimental costs and time.

5. How can thermodynamic principles be applied to improve the energy efficiency of buildings and urban infrastructure?
Answer: Thermodynamic analysis can optimize heating, ventilation, and air conditioning (HVAC) systems, improve insulation, and enhance energy management in buildings. Smart control systems based on these principles can reduce energy consumption, lower operational costs, and contribute to sustainable urban development.

6. What are the potential impacts of scaling thermodynamic processes from laboratory to industrial scale?
Answer: Scaling up introduces challenges such as increased energy losses, complex fluid dynamics, and material limitations. Overcoming these issues through innovative design and advanced simulation tools can lead to more efficient large-scale energy conversion and chemical production processes.

7. How might advances in nanotechnology and materials science influence thermodynamic efficiency in industrial systems?
Answer: Nanomaterials can offer superior thermal properties, such as enhanced conductivity or insulation, and improved catalyst performance. Incorporating these materials into energy systems could boost efficiency, reduce losses, and enable new applications in power generation and chemical processing.

8. In what ways could thermodynamic optimization contribute to mitigating climate change?
Answer: By designing processes that maximize energy efficiency and reduce waste heat, thermodynamic optimization can lower greenhouse gas emissions. Improvements in power generation, industrial processes, and transportation through thermodynamic innovations can significantly impact climate change mitigation efforts.

9. How can real-time monitoring and control, based on thermodynamic principles, enhance the performance of power plants?
Answer: Real-time data analysis allows for dynamic adjustments in operating conditions to maintain optimal efficiency. Implementing advanced control systems based on thermodynamic feedback can lead to more stable power output, lower fuel consumption, and reduced environmental impact.

10. What challenges exist in modeling non-equilibrium thermodynamic processes in complex systems, and how can they be addressed?
Answer: Non-equilibrium processes involve time-dependent and fluctuating behavior that is difficult to model accurately. Advances in computational methods, such as molecular dynamics and Monte Carlo simulations, along with machine learning techniques, can improve predictions and provide deeper insights into dynamic systems.

11. How might interdisciplinary approaches between thermodynamics and data science revolutionize industrial process optimization?
Answer: Integrating thermodynamic models with big data analytics and machine learning can lead to predictive maintenance, real-time process optimization, and adaptive control systems. This interdisciplinary approach can enhance efficiency, reduce downtime, and enable proactive management of complex industrial operations.

12. What ethical and societal considerations arise from the implementation of advanced thermodynamic technologies in energy and manufacturing sectors?
Answer: As energy systems become more efficient and automated, issues such as job displacement, resource allocation, and environmental impact must be addressed. Ethical considerations include ensuring equitable access to technology, maintaining transparency in energy policies, and balancing economic growth with sustainability and social well-being.

Engineering Thermodynamics: Numerical Problems and Solutions

1. Calculate the energy (in joules) of a photon with a wavelength of 600 nm using E = hc/λ. (h = 6.626×10⁻³⁴ J·s, c = 3.0×10⁸ m/s)
Solution:
λ = 600 nm = 600×10⁻⁹ m
E = (6.626×10⁻³⁴ J·s × 3.0×10⁸ m/s) / (600×10⁻⁹ m)
= (1.9878×10⁻²⁵ J·m) / (600×10⁻⁹ m)
≈ 3.313×10⁻¹⁹ J.

2. For a chemical reaction with ΔH = -100 kJ/mol and ΔS = -200 J/(mol·K) at 300 K, calculate the Gibbs free energy change ΔG.
Solution:
ΔG = ΔH – TΔS
= (-100,000 J/mol) – 300×(-200 J/(mol·K))
= -100,000 + 60,000
= -40,000 J/mol.

3. Calculate the Carnot efficiency for a heat engine operating between 700 K and 300 K.
Solution:
η = 1 – T_c/T_h
= 1 – 300/700
≈ 1 – 0.4286
≈ 0.5714 or 57.14%.

4. Determine the change in entropy when 400 J of heat is added reversibly at 350 K.
Solution:
ΔS = Q/T = 400 J / 350 K ≈ 1.143 J/K.

5. A power plant produces 500 MW of power and operates at an efficiency of 40%. Calculate the total heat input required.
Solution:
Efficiency η = W/Q_in, so Q_in = W/η
= (500×10⁶ W) / 0.40
= 1.25×10⁹ W.

6. For an ideal gas undergoing an isothermal expansion at 400 K from 1.0 L to 4.0 L (1 L = 0.001 m³) for 1 mole, calculate the work done. (R = 8.314 J/(mol·K))
Solution:
W = nRT ln(V_f/V_i)
= 1×8.314×400×ln(4.0/1.0)
= 3325.6×ln(4)
≈ 3325.6×1.386
≈ 4606 J.

7. A gas undergoes an adiabatic process with γ = 1.3. If the initial temperature is 500 K and the volume is halved, find the final temperature using TV^(γ–1) = constant.
Solution:
T₁V₁^(γ–1) = T₂V₂^(γ–1)
V₂ = 0.5V₁
T₂ = T₁ (V₁/V₂)^(γ–1) = 500 × (1/0.5)^(0.3)
= 500 × (2)^(0.3)
≈ 500 × 1.231
≈ 615.5 K.

8. Calculate the equilibrium constant K for a reaction at 400 K if ΔG = -20 kJ/mol. (R = 8.314 J/(mol·K))
Solution:
ΔG = -RT ln K
-20,000 J/mol = -8.314×400 ln K
ln K = 20,000 / (8.314×400)
= 20,000 / 3325.6
≈ 6.012
K = e^(6.012) ≈ 409.

9. Determine the internal energy change ΔU for a system where 800 J of heat is added and 300 J of work is done by the system.
Solution:
ΔU = Q – W = 800 J – 300 J = 500 J.

10. A system has a partition function Z = 100 at T = 350 K. Calculate its Helmholtz free energy F using F = –k_BT ln(Z). (k_B = 1.38×10⁻²³ J/K)
Solution:
F = –1.38×10⁻²³×350×ln(100)
ln(100) ≈ 4.6052
F ≈ –1.38×10⁻²³×350×4.6052
≈ –2.23×10⁻²⁰ J.

11. In a simulation, 2×10⁶ iterations take 0.05 s each. Calculate the total simulation time.
Solution:
Total time = 2×10⁶ × 0.05 s = 100,000 s.

12. A chemical reaction has a latent heat of vaporization of 2.26×10⁶ J/kg. How much energy is required to vaporize 0.75 kg of a substance?
Solution:
Energy = latent heat × mass
= 2.26×10⁶ J/kg × 0.75 kg
= 1.695×10⁶ J.