Topic 5: Projectile Motion
Course: Prep4Uni Physics 1
Chapter 1: Quantities and Measurement
Chapter 2: Forces and Moments
Chapter 3: Motion and Forces
Chapter 4: Energy and Fields
Chapter 5: Projectile Motion
🚁Projectile Motion: Overview
This topic focuses on the motion of objects under the influence of gravity, especially when launched with an initial horizontal or angled velocity. It also introduces the effects of air resistance and the concept of terminal velocity, helping you develop both qualitative and quantitative understanding of real-world projectile motion.
📖 Projectile Motion: Contents
- Free Fall and Gravitational Acceleration
Gravitational Potential Energy
Analyzing Projectile Motion
Air Resistance and Terminal Velocity
Qualitative Description of Motion with Air Resistance
🎯Projectile Motion: Learning Outcomes
By the end of this section, students should be able to:
Understand weight as a force in a gravitational field
Analyze motion with perpendicular velocity and acceleration components
Derive and use the gravitational potential energy equation: ΔEp = mgΔh
Describe the qualitative effects of air resistance on motion
Understand the concept of terminal velocity
Table of Contents
🔢1. Free Fall and Gravitational Acceleration
Key idea — free fall. In the absence of air resistance, all objects fall with the same
acceleration due to gravity (near Earth g ≈ 9.8 m s−2), regardless of mass.
- Weight (force due to gravity): W = m g.
- Units: W in newtons (N); m in kilograms (kg); g in N kg−1 (equivalently m s−2).
- Direction: g points toward Earth’s centre (downward near the surface).
Worked example. A 3 kg object in free fall experiences a weight of:
- W = m g = 3 × 9.8 = 29.4 N.
📐 Learning-Check 1.
Q: What is the weight of a 4 kg object on Earth?
A: W = m g = 4 × 9.8 = 39.2 N.
Q: What is the weight of a 4 kg object on Earth?
A: W = m g = 4 × 9.8 = 39.2 N.
📐 Learning-Check 2.
Q: True or False: A heavier object falls faster than a lighter one in free fall.
A: False — in a vacuum, all objects fall at the same rate (g).
Q: True or False: A heavier object falls faster than a lighter one in free fall.
A: False — in a vacuum, all objects fall at the same rate (g).
🔢2. Gravitational Potential Energy
Gravitational Potential Energy (GPE).
Near Earth’s surface the change in gravitational potential energy is
ΔEp = m g Δh,
where m is mass (kg), g ≈ 9.8 m s−2, and Δh is the change in height (m).
- Energy conversion in free fall: GPE ↓ while kinetic energy (KE) ↑.
- Total mechanical energy (GPE + KE) stays constant if air resistance is negligible.
Worked example. A 1.5 kg rock falls 10 m.
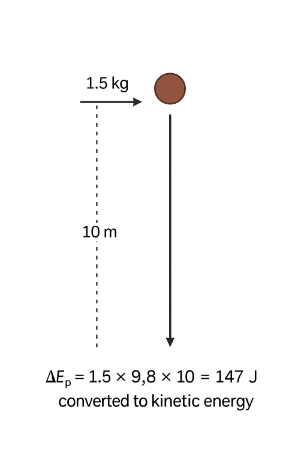
- ΔEp = m g Δh = 1.5 × 9.8 × 10 = 147 J (converted to KE).
📐 Learning-Check 1.
Q: A 0.8 kg object is lifted 2.5 m. What is its gain in potential energy?
A: ΔEp = m g Δh = 0.8 × 9.8 × 2.5 = 19.6 J.
Q: A 0.8 kg object is lifted 2.5 m. What is its gain in potential energy?
A: ΔEp = m g Δh = 0.8 × 9.8 × 2.5 = 19.6 J.
📐 Learning-Check 2.
Q: What energy change occurs as an object falls freely (ignore air resistance)?
A: GPE decreases while KE increases; total mechanical energy is (approximately) conserved.
Q: What energy change occurs as an object falls freely (ignore air resistance)?
A: GPE decreases while KE increases; total mechanical energy is (approximately) conserved.
🔢3. Analyzing Projectile Motion
Key ideas. In ideal projectile motion (ignore air resistance):
- Horizontal motion has constant velocity (no horizontal force).
- Vertical motion has constant acceleration due to gravity (a = ±g).
- Horizontal and vertical motions are independent and linked only by the same time t.
Vertical-motion equations (constant acceleration):
- v = u + at
- s = ut + ½at2
- v2 = u2 + 2as
Derivation 1 — v = u + at
- Acceleration is the rate of change of velocity: a = ( v − u ) / t.
- Rearrange: v − u = at ⇒ v = u + at.
Sign choice in vertical motion: upward throw ⇒ a = −g; downward fall ⇒ a = +g (if down is positive).
Derivation 2 — s = ut + ½at²
- Average velocity with constant a: vavg = ( u + v ) / 2.
- Displacement s = vavgt. Substitute v = u + at: s = [ u + ( u + at ) ]/2 · t = ut + ½at2.
Derivation 3 — v² = u² + 2as
- From Derivation 1, t = ( v − u ) / a.
- Use s = ( u + v )/2 · t and eliminate t: s = ( u + v )/2 · ( v − u ) / a = ( v2 − u2 ) / (2a) ⇒ v2 = u2 + 2as.
Worked example (horizontal launch).
A ball is thrown horizontally at 10 m/s from a height of 20 m.
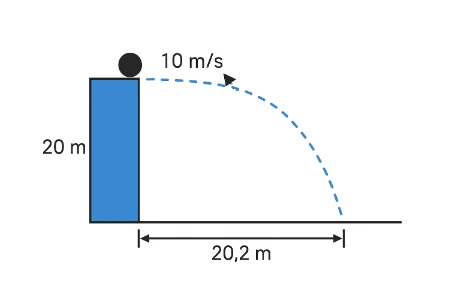
A ball is thrown horizontally at 10 m/s from a height of 20 m.
- Vertical time from s = ½gt²: t = √(2s/g) = √(40/9.8) ≈ 2.02 s.
- Horizontal range (constant speed): R = vx t = 10 × 2.02 ≈ 20.2 m.
📐 Learning-Check 1.
Q: A ball is projected horizontally at 12 m/s and hits the ground after 3 s. How far did it travel horizontally?
A: R = vx t = 12 × 3 = 36 m.
Q: A ball is projected horizontally at 12 m/s and hits the ground after 3 s. How far did it travel horizontally?
A: R = vx t = 12 × 3 = 36 m.
📐 Learning-Check 2.
Q: In projectile motion, what causes vertical acceleration?
A: Gravity (magnitude g ≈ 9.8 m s−2).
Q: In projectile motion, what causes vertical acceleration?
A: Gravity (magnitude g ≈ 9.8 m s−2).
🔢4. Air Resistance and Terminal Velocity
Air resistance (drag) is a force from the air that opposes motion and increases with speed. It reduces a falling object’s acceleration from g toward 0 as speed builds up.
How drag depends on speed
- Low–moderate speeds: \( D \approx k\,v \) (approximately proportional to speed).
- Most real falls (bluff bodies): \( D = \frac{1}{2}\,\rho\,C_d\,A\,v^{2} \), where \( \rho \) is air density, \( C_d \) the drag coefficient, and \( A \) the cross-sectional area.
Terminal velocity
- As speed rises, drag grows until it equals weight: \( D = mg \).
- Then the net force is zero and the object falls at a constant speed called the terminal velocity \( v_{t} \).
- With quadratic drag: \( v_{t} = \sqrt{\frac{2\,m\,g}{\rho\,C_d\,A}} \).
What affects \( v_{t} \)?
- Mass \( m \): heavier → larger \( v_{t} \).
- Area/shape \( (A,\;C_d) \): bigger or “flatter” → more drag → smaller \( v_{t} \).
- Air density \( \rho \): denser air → more drag → smaller \( v_{t} \).
Worked example — skydiver
Take \( m = 80~\text{kg} \), \( \rho = 1.2~\text{kg}\,\text{m}^{-3} \), and \( C_d A \approx 0.70~\text{m}^{2} \) (belly-to-earth).
\[ v_{t} \;=\; \sqrt{\frac{2\,m\,g}{\rho\,C_d\,A}} \;=\; \sqrt{\frac{2\cdot 80 \cdot 9.8}{1.2 \cdot 0.70}} \;\approx\; 43~\text{m}\,\text{s}^{-1} \;(\,\approx 155~\text{km}\,\text{h}^{-1}\,). \]
Take \( m = 80~\text{kg} \), \( \rho = 1.2~\text{kg}\,\text{m}^{-3} \), and \( C_d A \approx 0.70~\text{m}^{2} \) (belly-to-earth).
\[ v_{t} \;=\; \sqrt{\frac{2\,m\,g}{\rho\,C_d\,A}} \;=\; \sqrt{\frac{2\cdot 80 \cdot 9.8}{1.2 \cdot 0.70}} \;\approx\; 43~\text{m}\,\text{s}^{-1} \;(\,\approx 155~\text{km}\,\text{h}^{-1}\,). \]
Example narrative
A skydiver accelerates rapidly just after exiting (drag small), then more slowly as drag increases with speed. When drag balances weight, \( D = mg \), acceleration becomes zero and the speed remains constant at \( v_{t} \).
📐 Learning-Check 1.
Q: What happens to the net force when terminal velocity is reached?
A: It becomes zero since \( D = mg \) and the forces balance.
Q: What happens to the net force when terminal velocity is reached?
A: It becomes zero since \( D = mg \) and the forces balance.
📐 Learning-Check 2.
Q: Why do objects with larger surface area reach lower terminal velocities?
A: Larger \( A \) increases drag \( (D \propto A) \), so balance with weight occurs at a smaller speed.
Q: Why do objects with larger surface area reach lower terminal velocities?
A: Larger \( A \) increases drag \( (D \propto A) \), so balance with weight occurs at a smaller speed.
🔢5. Qualitative Description of Motion with Air Resistance
Big picture: Drag from the air opposes motion and grows with speed, so projectiles no longer trace perfect parabolas. The path becomes asymmetric: a gentle climb and a steeper descent, with shorter range and lower peak height than in a vacuum.
Without Air Resistance (idealized)
- Path is a symmetric parabola.
- Horizontal speed is constant; vertical motion has acceleration −g.
- Maximum range at 45° (for level launch/landing).
- Time up = time down (for same levels).
With Air Resistance (real world)
- Path is asymmetric (flatter rise, steeper fall).
- Horizontal speed decreases continuously due to drag.
- Peak height and range both decrease.
- Angle for maximum range is < 45° (often ~35–42° depending on drag).
- Time of flight usually shorter for the same launch conditions.
What controls the effect of drag?
- Shape & area (A) and drag coefficient (Cd): bigger/flatter → more drag.
- Speed: drag grows with speed (often ~v²), so high-speed projectiles deviate more.
- Air density (ρ): denser air (low altitude, cold weather) → more drag.
- Mass (m): heavier projectiles are less affected (higher momentum for the same area).
Worked comparison (qualitative):
Two balls launched at the same speed and angle: a light foam ball and a dense steel ball of the same size.
The foam ball loses horizontal speed much faster, so its range and peak height are far smaller; the steel
ball flies closer to the vacuum parabola (though still reduced).
Two balls launched at the same speed and angle: a light foam ball and a dense steel ball of the same size.
The foam ball loses horizontal speed much faster, so its range and peak height are far smaller; the steel
ball flies closer to the vacuum parabola (though still reduced).
📐 Learning-Check 1
Q: Describe how air resistance changes the trajectory of a projectile.
A: Drag makes the path asymmetric, with a shorter range and
lower maximum height than the vacuum parabola.
Q: Describe how air resistance changes the trajectory of a projectile.
A: Drag makes the path asymmetric, with a shorter range and
lower maximum height than the vacuum parabola.
📐 Learning-Check 2
Q: How does the downward part of the motion differ with air resistance?
A: The projectile accelerates less rapidly than g at first because
upward drag opposes the fall; as speed grows, drag increases and the motion can approach a terminal-like behavior.
Q: How does the downward part of the motion differ with air resistance?
A: The projectile accelerates less rapidly than g at first because
upward drag opposes the fall; as speed grows, drag increases and the motion can approach a terminal-like behavior.
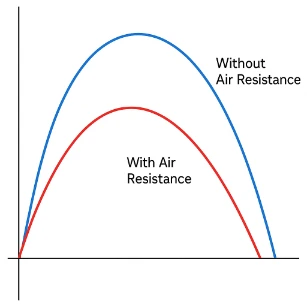
Big picture: Drag from the air opposes motion and grows with speed, so projectiles no longer trace perfect parabolas. The path becomes asymmetric: a gentle climb and a steeper descent, with shorter range and lower peak height than in a vacuum.
Without Air Resistance (idealized)
- Path is a symmetric parabola.
- Horizontal speed is constant; vertical motion has acceleration −g.
- Maximum range at 45° (for level launch/landing).
- Time up = time down (for same levels).
With Air Resistance (real world)
- Path is asymmetric (flatter rise, steeper fall).
- Horizontal speed decreases continuously due to drag.
- Peak height and range both decrease.
- Angle for maximum range is < 45° (typically 35–42° depending on drag).
- Time of flight usually shorter for the same launch conditions.
What controls the effect of drag?
- Shape & area (A) and drag coefficient (Cd): bigger/flatter → more drag.
- Speed: drag grows with speed (often ~v²), so high-speed projectiles deviate more.
- Air density (ρ): denser air (low altitude, cold weather) → more drag.
- Mass (m): heavier projectiles are less affected (higher momentum for the same area).
Worked comparison (qualitative):
Two balls launched at the same speed and angle: a light foam ball and a dense steel ball of the same size.
The foam ball loses horizontal speed much faster, so its range and peak height are far smaller; the steel
ball flies closer to the vacuum parabola (though still reduced).
Two balls launched at the same speed and angle: a light foam ball and a dense steel ball of the same size.
The foam ball loses horizontal speed much faster, so its range and peak height are far smaller; the steel
ball flies closer to the vacuum parabola (though still reduced).
📐 Learning-Check 1
Q: Describe how air resistance changes the trajectory of a projectile.
A: Drag makes the path asymmetric, with a shorter range and
lower maximum height than the vacuum parabola.
Q: Describe how air resistance changes the trajectory of a projectile.
A: Drag makes the path asymmetric, with a shorter range and
lower maximum height than the vacuum parabola.
📐 Learning-Check 2
Q: How does the downward part of the motion differ with air resistance?
A: The projectile accelerates less rapidly than g at first because
upward drag opposes the fall; as speed grows, drag increases until approaching terminal-like behavior.
Q: How does the downward part of the motion differ with air resistance?
A: The projectile accelerates less rapidly than g at first because
upward drag opposes the fall; as speed grows, drag increases until approaching terminal-like behavior.
⚙️Key Concepts Recap
Go back to Prep4Uni Physics 1
Additional Resources:
To deepen your understanding, you are strongly encouraged to explore the materials provided on the following pages.
📝EXERCISES
Questions and Answers
🟢 Section 1: Free Fall and Gravitational Acceleration
-
What is the value of acceleration due to gravity near Earth’s surface?
Answer: Approximately 9.8 m/s2 downward.
Why: Near Earth’s surface, the gravitational field strength is ~9.8 N/kg, which produces the same numerical value for acceleration on freely falling objects in a vacuum. -
An object is dropped from rest. How long will it take to fall 19.6 m?
Answer: s = ½g t2 ⇒ t = √(2s/g) = √(39.2/9.8) = 2 s.
Why: With zero initial speed, displacement grows with t2 under constant acceleration. -
A 3 kg object is in free fall. What is its weight?
Answer: W = mg = 3 × 9.8 = 29.4 N (downward).
Why: Weight is the gravitational force; mass times gravitational field strength. -
True or False: A heavier object falls faster than a lighter one in a vacuum.
Answer: False — both accelerate at g if air resistance is negligible.
Why: Gravity’s force is larger for heavier objects, but so is inertia; the effects cancel in a = F/m. -
What kind of motion does an object in free fall undergo?
Answer: Uniformly accelerated motion under gravity (a = g).
Why: The gravitational field is (approximately) constant near Earth’s surface.
🟢 Section 2: Gravitational Potential Energy
-
Write the equation for gravitational potential energy change.
Answer: ΔEp = m g Δh.
Why: Lifting against gravity increases energy in proportion to mass and height change. -
A 2 kg object is lifted from 1 m to 4 m. What is the gain in potential energy?
Answer: ΔEp = 2 × 9.8 × (4 − 1) = 58.8 J.
Why: Only the change in height matters for ΔEp. -
If a 5 kg rock falls 6 m, how much GPE is converted to kinetic energy?
Answer: ΔEp = 5 × 9.8 × 6 = 294 J (to KE, ignoring air resistance).
Why: In free fall, lost GPE becomes kinetic energy (energy conservation). -
What energy transformation occurs during free fall?
Answer: GPE decreases; KE increases by the same amount (ideal case).
Why: Total mechanical energy is conserved when non-conservative forces are negligible. -
At the highest point of a vertical throw, what is the object’s KE and GPE?
Answer: KE = 0; GPE = maximum (relative to the release point).
Why: Vertical speed is momentarily zero at the top; all energy is stored as GPE.
🟢 Section 3: Analyzing Projectile Motion
-
What are the horizontal and vertical components of motion in a projectile?
Answer: Horizontal: constant velocity; Vertical: uniform acceleration (g downward).
Why: Gravity acts vertically; there’s no horizontal force (ideal model). -
A ball is thrown horizontally at 10 m/s from a 20 m high cliff. How far from the base does it land?
Answer: Flight time t = √(2h/g) = √(40/9.8) ≈ 2.02 s → Range = 10 × 2.02 ≈ 20.2 m.
Why: Horizontal and vertical motions are independent; time comes from vertical drop. -
True or False: Gravity affects only the vertical component of projectile motion.
Answer: True (in the ideal no-air-resistance model).
Why: Gravity is a vertical force; horizontal acceleration is zero. -
What is the vertical acceleration of a projectile at the top of its path?
Answer: 9.8 m/s2 downward.
Why: Acceleration is due to gravity and does not vanish at the apex—even when vertical speed is zero. -
A projectile is launched at an angle. What shape does its path take (ideal case)?
Answer: A symmetric parabola (ignoring air resistance).
Why: Combining constant horizontal velocity with uniformly accelerated vertical motion yields a parabolic trajectory.
🟢 Section 4: Air Resistance and Terminal Velocity
-
What is air resistance?
Answer: A friction-like drag force opposing motion through air; it grows with speed and depends on shape/area and air density.
Why: Moving objects push on air; the resulting fluid forces act opposite motion. -
What is terminal velocity?
Answer: The constant speed reached when drag equals weight (Fdrag = mg), so net force and acceleration are zero.
Why: With forces balanced, there’s no further change in speed. -
True or False: Terminal velocity occurs when net force becomes zero.
Answer: True — that’s precisely the condition for terminal motion.
Why: Zero net force implies zero acceleration, hence steady speed. -
What two forces act on a falling object with air resistance?
Answer: Weight (downward) and air resistance (upward).
Why: Gravity pulls down; the fluid pushes back against motion. -
Why do skydivers initially accelerate and then fall at constant speed?
Answer: At first, mg > drag → acceleration. As speed builds, drag increases until drag = mg → terminal velocity (constant speed).
Why: Drag depends on speed (roughly ∝ v or v2), so it grows until it balances weight.
🟢 Section 5: Qualitative Effects of Air Resistance
-
Describe the effect of air resistance on the range of a projectile.
Answer: Range is reduced compared with the ideal case.
Why: Drag removes kinetic energy and slows the horizontal component, shortening the distance traveled. -
How does air resistance affect time of flight?
Answer: It often decreases for angled launches (slows ascent and speeds descent), but can increase slightly in near-vertical drops where drag quickly counters gravity.
Why: The balance between reduced upward motion and altered downward speed depends on angle and speed regime. -
What happens to the trajectory shape due to air resistance?
Answer: It becomes asymmetric, with a steeper, shorter descent path than ascent.
Why: Drag continually removes speed, especially near the end of flight. -
Why does a feather fall slower than a stone in air?
Answer: A feather has far greater drag relative to weight than a stone, so it reaches a much lower terminal speed.
Why: Large area and low mass give a high drag-to-weight ratio. -
How does surface area affect terminal velocity?
Answer: Larger area → more drag → lower terminal velocity (all else equal).
Why: Drag is roughly proportional to cross-sectional area and the square of speed in typical conditions.
Problems and Solutions
-
A stone is dropped from rest from a cliff. How fast is it moving after 4 seconds?
Solution: Given u=0, a=9.8 m/s2, t=4 s. Use v=u+a t ⇒ v=0+9.8×4=39.2 m/s downward.
Why: In free fall with negligible air resistance, speed increases linearly with time under constant acceleration g. -
A ball is thrown upward at 20 m/s. How high does it rise before stopping momentarily?
Solution: At the top, v=0. Use v2=u2+2a s with a=−9.8 m/s2:
0 = 202 + 2(−9.8)s ⇒ s=400/19.6=20.41 m.
Why: Upward motion decelerates at magnitude g until vertical speed becomes zero at the peak. -
How long does it take the ball in Q2 to reach the highest point?
Solution: Use v=u+a t: 0 = 20 − 9.8t ⇒ t=20/9.8=2.04 s.
Why: Time to peak is initial speed divided by the (downward) acceleration magnitude. -
A car accelerates uniformly from rest at 2 m/s². How far does it travel in 10 s?
Solution: u=0, a=2, t=10. Use s=u t+½a t2 ⇒ s=0+0.5×2×100=100 m.
Why: With constant acceleration from rest, distance grows with t2. -
A rock falls freely and travels 45 m. Find its final speed before hitting the ground.
Solution: u=0, s=45 m, a=9.8. Use v2=2a s ⇒ v=√(2×9.8×45)=√882=29.7 m/s (downward).
Why: Starting from rest under constant acceleration, speed depends on drop height via energy/work equivalence. -
A runner slows from 8 m/s to 2 m/s with uniform deceleration 1.5 m/s². How long does it take?
Solution: Use v=u+a t: 2 = 8 + (−1.5)t ⇒ t=(2−8)/(−1.5)=4.0 s.
Why: Negative acceleration (deceleration) reduces speed linearly in time. -
A projectile is launched vertically with initial speed 15 m/s. Find the time to return to the ground.
Solution: Time to rise tup=u/g=15/9.8≈1.53 s. Total time ≈ 3.06 s.
Why: Symmetry (ignore air): ascent time equals descent time back to launch level. -
What is the total displacement of the projectile in Q7 after 3.06 s?
Solution: It returns to its launch level ⇒ displacement = 0 m.
Why: Displacement is final position minus initial; same level gives zero. -
A ball is dropped from 30 m high. How long does it take to hit the ground?
Solution: Use s=½g t2: 30 = 0.5×9.8×t2 ⇒ t2=6.122 ⇒ t=2.47 s.
Why: From rest with constant g, time grows with √height. -
A bullet is fired upward at 50 m/s. How long before it is 60 m above the launch point?
Solution: Use s=u t+½a t2 with a=−9.8: 60 = 50t − 4.9t2 ⇒ 4.9t2 − 50t + 60 = 0.
Quadratic formula ⇒ t ≈ 1.34 s (on the way up) or 9.11 s (on the way down).
Why: The projectile passes the same height twice (ascending and descending) in the ideal model. -
A rocket goes from 0 to 60 m/s in 6 s. What is its acceleration and distance covered?
Solution: a=(v−u)/t=(60−0)/6=10 m/s2.
Distance: s=u t+½a t2=0+0.5×10×36=180 m.
Why: Constant acceleration kinematics; distance grows with t2. -
A cyclist decelerates from 12 m/s to rest in 4 s. What distance is covered?
Solution: a=(0−12)/4=−3 m/s2. Then s=u t+½a t2=12×4+0.5×(−3)×16=48−24=24 m.
Why: Negative acceleration reduces speed; the average speed over the interval is (12+0)/2=6 m/s; 6×4=24 m (same result). -
A ball is thrown downward at 5 m/s from a height of 25 m. What is its speed just before hitting the ground?
Solution: Take downward positive. Use v2=u2+2a s ⇒ v2=52+2×9.8×25=25+490=515 ⇒ v=22.7 m/s (downward).
Why: Initial downward speed adds to the gain from gravitational acceleration. -
An object takes 3 seconds to hit the ground after falling. What height did it fall from?
Solution: s=½g t2=0.5×9.8×9=44.1 m.
Why: From rest under constant g, distance depends on the square of time. -
A motorbike speeds up from 15 m/s to 30 m/s in 5 s. Find its acceleration and distance covered.
Solution: a=(30−15)/5=3 m/s2.
s=u t+½a t2=15×5+0.5×3×25=75+37.5=112.5 m.
Why: Distance equals average speed × time; average speed here is (15+30)/2=22.5 m/s; 22.5×5=112.5 m. -
A falling object reaches 40 m/s after falling 50 m. What was its initial velocity?
Solution: Use v2=u2+2a s: 1600 = u2 + 2×9.8×50 = u2 + 980 ⇒ u2=620 ⇒ u=24.9 m/s downward.
Why: A nonzero initial speed is required if the final speed after a given drop is less than √(2g s). -
A diver jumps vertically upwards at 6 m/s. What maximum height does she reach?
Solution: 0 = 62 + 2(−9.8)s ⇒ s=36/19.6=1.84 m.
Why: Convert initial kinetic energy to gravitational potential energy (same result as constant-g kinematics). -
A particle is projected upward and reaches maximum height after 2.5 s. What was its initial velocity?
Solution: At the top, v=0. Use v=u+a t: 0=u−9.8×2.5 ⇒ u=24.5 m/s (upward).
Why: Time to peak equals initial speed divided by g. -
How long does it take an object thrown upward at 10 m/s to fall back to the same level?
Solution: Up time tup=10/9.8≈1.02 s ⇒ total time ≈ 2.04 s.
Why: Ideal symmetry of projectile motion about the highest point. -
A stone is thrown vertically upward and reaches a height of 45 m. What was its launch speed?
Solution: 0 = u2 − 2×9.8×45 ⇒ u2=882 ⇒ u=29.7 m/s (upward).
Why: Initial kinetic energy equals the gain in gravitational potential energy at the top.
Have feedback or questions? We’d love to hear from you!
Course: Prep4Uni Physics 1
Chapter 1: Quantities and Measurement
Chapter 2: Forces and Moments
Chapter 3: Motion and Forces
Chapter 4: Energy and Fields
Chapter 5: Projectile Motion