Topic 3: Motion and Forces
Course: Prep4Uni Physics 1
Chapter 1: Quantities and Measurement
Chapter 2: Forces and Moments
Chapter 3: Motion and Forces
Chapter 4: Energy and Fields
Chapter 5: Projectile Motion
🚁Overview
This topic develops your understanding of how and why objects move. It connects the description of motion (kinematics) with the forces that cause motion, using Newton’s Laws as a foundation for analyzing dynamics in real-world and theoretical situations.
📖Contents
- Kinematics and uniformly accelerated motion
- Linear momentum
- Newton’s Laws of Motion
🎯Learning Outcomes
By the end of this section, students should be able to:
- Define and use terms: displacement, speed, velocity, and acceleration
- Use and interpret motion-time and velocity-time graphs
- Derive and apply the kinematic equations for uniformly accelerated motion
- Understand mass as a measure of inertia
- Define and use momentum in practical situations
- Apply Newton’s Laws to explain and predict motion
- Solve problems using Newton’s Second Law: F = ma
Table of Contents
🔢1. Kinematics and Uniformly Accelerated Motion
Key concepts.- Displacement \( (s) \): change in position (vector; includes direction).
- Speed \( (v) \): scalar rate of motion; \( v=\frac{\text{distance}}{\text{time}} \).
- Velocity \( (v) \): vector rate of change of position (magnitude + direction).
- Acceleration \( (a) \): rate of change of velocity; \( a=\frac{\Delta v}{\Delta t} \).
- \( v = u + a t \) (vector form: \( \vec v=\vec u+\vec a\,t \)).
- \( s = u t + \frac12 a t^{2} \) (area under the \(v\)-\(t\) graph).
- \( v^{2} = u^{2} + 2 a s \) (useful when time \( t \) is unknown).
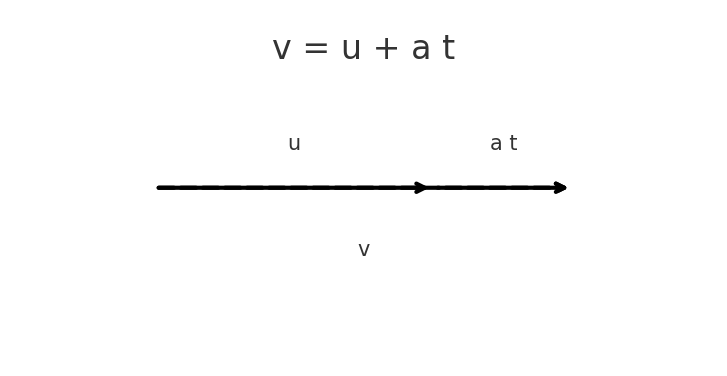
Vector relation: \( \vec v = \vec u + \vec a\,t \).

Displacement from \( v\!-\!t \) graph: \( s = u t + \frac12 a t^{2} \).
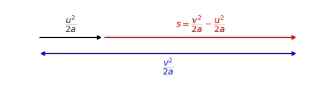
When \( t \) is unknown: \( v^{2} = u^{2} + 2 a s \).
- Use \( a=\frac{v-u}{t} \).
- \( a=\frac{30-10}{5}=4~\text{m s}^{-2}. \)
Answer: \( 4~\text{m s}^{-2} \).
- At the top, \( v=0 \). Take upward \( + \), use \( a=-g\approx-9.8~\text{m s}^{-2} \).
- \( t=\frac{v-u}{a}=\frac{0-15}{-9.8}\approx 1.53~\text{s}. \)
Answer: \( \approx 1.53~\text{s} \).
- First \( a=\frac{25-0}{10}=2.5~\text{m s}^{-2} \).
- Then \( s=u t+\frac12 a t^{2}=0+\frac12(2.5)(10^{2})=125~\text{m}. \)
Answer: \( 125~\text{m} \).
Exam tip: choose a clear sign convention (e.g., upward \(+\)) and stick to it; check units at each step (\(\text{m}, \text{s}, \text{m s}^{-1}, \text{m s}^{-2}\)).
🔢2. Interpreting Motion Graphs
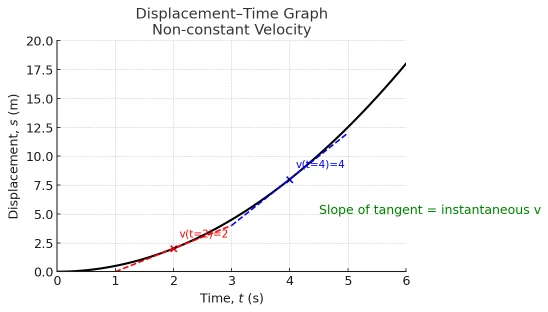
Displacement–time graph (s–t).- Slope = instantaneous velocity: \( v=\frac{\Delta s}{\Delta t} \) for a straight segment, \( v(t)=\frac{ds}{dt} \) in general.
- Horizontal line ⇒ \( v=0 \) (object at rest). Steeper line ⇒ larger speed.
- Positive slope ⇒ motion in + direction; negative slope ⇒ motion in − direction.
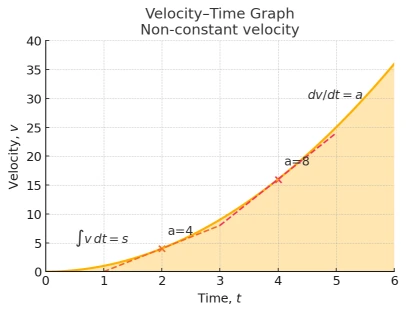
- Slope = acceleration: \( a=\frac{\Delta v}{\Delta t} \) for a straight segment, \( a(t)=\frac{dv}{dt} \) in general.
- Area under the curve = displacement over an interval: \( s=\int_{t_1}^{t_2} v(t)\,dt \).
- Horizontal line ⇒ constant velocity (\( a=0 \)). A rising line through \( v=0 \) ⇒ speeding up in the + direction.
- Acceleration (slope): \( a=\frac{\Delta v}{\Delta t}=\frac{20-0}{4-0}=5~\text{m s}^{-2} \).
- Displacement (area of triangle): \( s=\frac12\times\text{base}\times\text{height}=\frac12\times 4\times 20=40~\text{m} \).
Answer: \( a=5~\text{m s}^{-2} \), \( s=40~\text{m} \).
Answer: Constant velocity (\( a=0 \)).
Answer: Displacement over that time interval, \( s=\int v(t)\,dt \).
🔢3. Newton’s Laws of Motion
First Law (Inertia): A body remains at rest or moves with constant velocity when the net external force is zero. In symbols: \( \sum \vec F = \vec 0 \Rightarrow \vec v = \text{constant} \).
Second Law (Dynamics): Net force equals mass times acceleration: \( \sum \vec F = m\,\vec a \). More generally, \( \sum \vec F = \frac{d\vec p}{dt} \) with momentum \( \vec p = m\vec v \) (for constant \( m \Rightarrow m\,\vec a \)).
Third Law (Action–Reaction): Forces between two bodies are equal in magnitude and opposite in direction: \( \vec F_{A\to B} = -\,\vec F_{B\to A} \). They act on different bodies and therefore do not cancel in a single free-body diagram.
Units & components: \( [\vec F] = \text{kg m s}^{-2} = \text{N} \). Components: \( \sum F_x = m a_x,\ \sum F_y = m a_y \). Weight: \( W = m g \) (near Earth, \( g \approx 9.8~\text{m s}^{-2} \)).
- By the second law: \( F_{\text{net}} = m a = 3.0 \times 2.0 = 6.0~\text{N} \) in \(+x\).
- If several forces act (e.g., push \(P\) and friction \(f\)), then \( P – f = 6.0~\text{N} \). Knowing either \(P\) or \(f\) lets you solve for the other.
Answer: \( 6.0~\text{N} \) along \(+x\).
\( m = \frac{F}{a} = \frac{10}{5.0} = 2.0~\text{kg} \).
Newton’s First Law (Inertia) — bodies tend to maintain their current state of motion.
🔢4. Mass and Inertia
Mass (m) quantifies an object’s resistance to changes in its motion (inertia). For a given net force, acceleration is smaller when mass is larger: \( \vec a = \frac{\sum \vec F}{m} \).
Inertia is the tendency to maintain the current state of motion (rest or constant velocity). More mass ⟹ more inertia ⟹ harder to start/stop/turn.
Units & types of mass. SI unit: kilogram (kg). In everyday mechanics we treat inertial mass (resists acceleration) and gravitational mass (appears in \( W = m g \)) as numerically identical.
Mass vs weight. Mass (kg) is intrinsic; weight is a force: \( W = m g \) (newtons). On the Moon, \(g\) is smaller, so weight changes while mass stays the same.
- Cart A: \( a_A = \frac{F}{m_A} = \frac{12}{3.0} = 4.0~\text{m s}^{-2} \).
- Cart B: \( a_B = \frac{F}{m_B} = \frac{12}{6.0} = 2.0~\text{m s}^{-2} \).
- Conclusion: the lighter cart accelerates twice as much under the same force (less inertia).
Answer: \( a_A = 4.0~\text{m s}^{-2} \), \( a_B = 2.0~\text{m s}^{-2} \).
The lighter cart. From \( a = \frac{F}{m} \), smaller \(m\) gives larger \(a\) (less inertia).
Inertia (quantified by mass, unit kg). It appears in \( \sum \vec F = m \vec a \) and \( W = m g \).
🔢5. Linear Momentum
Definition (vector): linear momentum \( \vec p \) is \( \vec p = m\,\vec v \). Unit: kg·m·s\(^{-1}\).
Impulse–momentum theorem: The impulse delivered by a net force equals the change in momentum: \[ \vec J \equiv \int_{t_1}^{t_2} \vec F_{\text{net}}(t)\,dt = \Delta \vec p = \vec p_2 – \vec p_1. \] For an approximately constant force over \(\Delta t\): \( \vec F_{\text{avg}} = \frac{\Delta \vec p}{\Delta t} \).
Newton’s 2nd Law (momentum form): \( \vec F_{\text{net}} = \frac{d\vec p}{dt} \). For constant mass, \( \vec F_{\text{net}} = m\,\vec a \).
Conservation of momentum: In an isolated system (external net impulse \(= \vec 0\)), total momentum is conserved: \[ \sum \vec p_{\text{initial}} = \sum \vec p_{\text{final}}. \] Energy may or may not be conserved (elastic vs inelastic collisions).
- Initial momentum: \( \vec p_i = (2.0)(+3.0) = +6.0~\text{kg m s}^{-1} \).
- Final momentum: \( \vec p_f = 0 \Rightarrow \Delta \vec p = \vec p_f – \vec p_i = -6.0~\text{kg m s}^{-1} \) (opposite motion).
- Average force on trolley: \( \vec F_{\text{avg}} = \frac{\Delta \vec p}{\Delta t} = \frac{-6.0}{0.10} = -60~\text{N} \) (direction opposite the incoming motion).
Report: magnitude \(60~\text{N}\), directed opposite to the initial velocity.
- Before: \( p_i = (0.40)(+2.5) + (0.60)(0) = +1.00~\text{kg m s}^{-1} \).
- After (stuck): total mass \(= 1.00~\text{kg}\), speed \(v_f\) so \( p_f = (1.00)v_f \).
- Conservation: \( p_f = p_i \Rightarrow v_f = \frac{1.00}{1.00} = 1.00~\text{m s}^{-1} \) (to the right).
Answer: \( v_f = 1.00~\text{m s}^{-1} \) (perfectly inelastic; kinetic energy is not conserved).
\( p = m v = 0.50 \times 8.0 = 4.0~\text{kg m s}^{-1} \) (direction of motion).
Impulse: \( J = F\,\Delta t = 20 \times 0.20 = 4.0~\text{N s} = 4.0~\text{kg m s}^{-1} \).
Final speed: \( v = \frac{\Delta p}{m} = \frac{4.0}{0.40} = 10~\text{m s}^{-1} \).
⚙️Key Concepts Recap
| Concept | Formula | When / notes |
|---|---|---|
| Displacement (s) | \( s = u t + \frac{1}{2} a t^{2} \) | Uniform acceleration; area under \(v\)–\(t\) graph. |
| Final velocity (v) | \( v = u + a t \) | Vector form: \( \vec v = \vec u + \vec a\,t \). |
| Time-free kinematic | \( v^{2} = u^{2} + 2 a s \) | Use when \(t\) is unknown. |
| Average acceleration | \( a_{\text{avg}}=\frac{\Delta v}{\Delta t} \) | Slope of \(v\)–\(t\) graph on straight segments. |
| Displacement from \(v\)–\(t\) | \( s = \int_{t_1}^{t_2} v(t)\,dt \) | Area under the \(v\)–\(t\) curve; sign matters. |
| Newton’s 2nd Law | \( \sum \vec F = m\,\vec a \) | Momentum form: \( \sum \vec F = \frac{d\vec p}{dt} \). |
| Weight | \( W = m g \) | Near Earth, \( g \approx 9.8~\text{m s}^{-2} \). |
| Linear momentum | \( \vec p = m\,\vec v \) | Unit: kg·m·s\(^{-1}\); vector quantity. |
| Impulse | \( \vec J=\int \vec F\,dt=\Delta \vec p \) | For constant \(F\): \( \vec J=\vec F\,\Delta t \). |
Proceed to: Topic 4: Energy and Fields
Go back to Prep4Uni Physics 1
Additional Resources:
📝 EXERCISES
25 Learning-Check Questions & Answers
(5 from each of the 5 subsections in “Motion and Forces”)
- Q: What is the difference between distance and displacement?A: Distance is total path length (scalar). Displacement is straight-line change from start to finish (vector with direction).
- Q: A runner goes 200 m east then 150 m west. What are the total distance and displacement?A: Distance \(=200+150=350~\text{m}\). Displacement \(=200-150=50~\text{m}\) east.
- Q: Define speed and instantaneous velocity.A: Speed \(=\frac{\text{distance}}{\text{time}}\) (scalar). Instantaneous velocity \(=\frac{d\vec s}{dt}\) (vector rate of change of position).
- Q: A car covers \(180~\text{km}\) north in \(3~\text{h}\), then \(60~\text{km}\) east in \(1~\text{h}\). Find the average velocity vector (magnitude & direction).A: Displacement \(=(60,\,180)~\text{km}\). Total time \(=4~\text{h}\).
Magnitude \(=\frac{\sqrt{60^{2}+180^{2}}}{4}=\frac{189.74}{4}\approx 47.4~\text{km h}^{-1}\).
Direction \(=\arctan\!\big(\frac{180}{60}\big)\approx 71.6^\circ\) north of east. - Q: What is the physical meaning of a negative acceleration?A: The velocity’s magnitude decreases (deceleration) or the velocity is directed opposite the chosen positive direction.
- Q: On a displacement–time (s–t) graph, how do you tell if an object is accelerating?A: Non-linear (curved) graph ⇒ slope changes with time ⇒ acceleration present.
- Q: On a velocity–time (v–t) graph, what does the area under the curve represent?A: Displacement over that interval: \( s=\int v(t)\,dt\).
- Q: A v–t graph is a straight line from \((0,0)\) to \((5~\text{s},\,20~\text{m s}^{-1})\). What are the acceleration and distance traveled?A: \(a=\frac{\Delta v}{\Delta t}=\frac{20}{5}=4~\text{m s}^{-2}\). Distance \(=\frac12\times 5\times 20=50~\text{m}\). → Using \(\frac12\) as \(\frac12\).
- Q: What feature of a v–t graph indicates constant velocity?A: A horizontal line (zero slope ⇒ \(a=0\)).
- Q: How do you find instantaneous acceleration on an s–t graph?A: Acceleration \(= \frac{d^{2}s}{dt^{2}}\) (concavity). Upward curvature ⇒ \(a>0\).
- Q: State the three “suvat” equations for constant acceleration.A: \(v=u+at\); \(s=ut+\frac12 at^{2}\); \(v^{2}=u^{2}+2as\).
- Q: Derive \(s=\frac12 a t^{2}\) for motion from rest.A: With \(u=0\): \(s=ut+\frac12 at^{2}=0+\frac12 at^{2}\).
- Q: How long does a stone dropped from rest take to fall \(20~\text{m}\) ( \(g=9.8~\text{m s}^{-2}\) )?A: \(s=\frac12 g t^{2}\Rightarrow t=\sqrt{\frac{2s}{g}}=\sqrt{\frac{40}{9.8}}\approx 2.02~\text{s}\).
- Q: A car accelerates uniformly from \(10\) to \(30~\text{m s}^{-1}\) over \(50~\text{m}\). Find \(a\).A: \(v^{2}=u^{2}+2as\Rightarrow 30^{2}=10^{2}+2a(50)\Rightarrow a=8~\text{m s}^{-2}\).
- Q: If \(a=0\), which kinematic equations still hold?A: \(v=u\) (constant), \(s=ut\), and \(v^{2}=u^{2}\).
- Q: Define linear momentum and its SI unit.A: \(\vec p = m\vec v\). Unit: \(\text{kg·m s}^{-1}\).
- Q: What is impulse, and how is it related to momentum?A: Impulse \(J=\vec F\,\Delta t\); \(J=\Delta \vec p\).
- Q: A \(0.5~\text{kg}\) ball thrown at \(20~\text{m s}^{-1}\) has what momentum?A: \(p=0.5\times 20=10~\text{kg·m s}^{-1}\).
- Q: A constant \(5~\text{N}\) force acts for \(3~\text{s}\) on a \(1~\text{kg}\) mass initially at rest. What is the final speed?A: \(J=5\times 3=15~\text{N·s}=\Delta p=m\,\Delta v\Rightarrow v=15/1=15~\text{m s}^{-1}\).
- Q: State conservation of momentum for a closed system.A: Total momentum before \(=\) total momentum after, if no external forces act.
- Q: State Newton’s First Law.A: A body remains at rest or moves with constant velocity unless acted upon by a net external force.
- Q: Give a real-world example of Newton’s First Law.A: A hockey puck glides on nearly frictionless ice at constant speed in a straight line.
- Q: State Newton’s Second Law.A: \(\sum \vec F = m\,\vec a\).
- Q: What is the reaction force to the weight of a book on a table (Third Law)?A: The book exerts an equal-and-opposite downward force on the table.
- Q: A \(5~\text{kg}\) block is pushed with \(20~\text{N}\) across a frictionless floor. What is its acceleration?A: \(a=\frac{F}{m}=\frac{20}{5}=4~\text{m s}^{-2}\).
Tip: Keep a consistent sign convention, write units at each step, and check vector directions before substituting numbers.
20 Problems with Detailed Solutions
(Covering all five sections of “Motion and Forces”)
Section 1: Displacement & Kinematics
- Variable-Speed Journey
A car’s velocity is \(v(t)=4t\) (m/s) for \(0\le t\le 5\ \text{s}\).
a) Displacement from \(t=0\) to \(5\ \text{s}\).
b) Acceleration at \(t=2\ \text{s}\).Solution.
a) \( s=\int_{0}^{5} 4t\,dt=[2t^{2}]_{0}^{5}=50~\text{m}.\)
b) \( a=\frac{dv}{dt}=4~\text{m s}^{-2}\) (constant). - Change of Direction
A cyclist travels \(100~\text{m}\) east in \(20~\text{s}\), then \(60~\text{m}\) west in \(15~\text{s}\).
a) Total distance and displacement.
b) Average speed and average-velocity magnitude.Solution.
a) Distance \(=160~\text{m}\); Displacement \(=100-60=40~\text{m}\) east.
b) \(\text{Avg speed}=160/35\approx 4.57~\text{m s}^{-1}\);
\(\ |\vec v_{\text{avg}}|=40/35\approx 1.14~\text{m s}^{-1}\) east. - Instantaneous vs. Average
A particle’s position is \(s(t)=t^{3}-6t^{2}+9t\) (m).
a) Average velocity on \(t\in[1,3]\).
b) Instantaneous velocity at \(t=2~\text{s}\).Solution.
a) \(s(3)=0,\ s(1)=4 \Rightarrow \Delta s=-4,\ \Delta t=2\Rightarrow v_{\text{avg}}=-2~\text{m s}^{-1}.\)
b) \(v(t)=3t^{2}-12t+9\Rightarrow v(2)=-3~\text{m s}^{-1}.\) - Non-Uniform Motion
A runner’s speed increases uniformly from \(5\) to \(9~\text{m s}^{-1}\) in \(4~\text{s}\), then remains constant.
a) Sketch \(v\)–\(t\). b) Distance in first \(4~\text{s}\) and next \(6~\text{s}\).Solution.
a) Line from \((0,5)\) to \((4,9)\), then horizontal at \(v=9\).
b) First \(4~\text{s}\): trapezoid area \(=\frac{(5+9)}{2}\cdot 4=28~\text{m}\). Next \(6~\text{s}\): \(9\cdot 6=54~\text{m}\). - Rapid Deceleration
A car at \(25~\text{m s}^{-1}\) brakes with constant \(a=-5~\text{m s}^{-2}\).
a) Time to stop. b) Braking distance.Solution.
a) \(0=u+at\Rightarrow t=25/5=5~\text{s}\).
b) \(s=ut+\frac12 a t^{2}=25\cdot 5+\frac12(-5)\cdot 25=62.5~\text{m}\).
Section 2: Motion Graphs
- Piecewise \(v\)–\(t\) Analysis
Given \(v\)–\(t\): \(0\!\to\!4~\text{s}\) at \(2\) m/s; \(4\!\to\!6~\text{s}\) linear to \(6\) m/s; \(6\!\to\!10~\text{s}\) constant at \(6\) m/s. Find total displacement.
Solution. Areas: \(0\)–\(4\): \(2\cdot 4=8\). \(4\)–\(6\): trapezoid \(=\frac{2+6}{2}\cdot 2=8\). \(6\)–\(10\): \(6\cdot 4=24\). Total \(=40~\text{m}\). - Reading \(s\)–\(t\) Curves
\(s(t)=2t^{2}\).
a) \(v\) at \(t=3~\text{s}\). b) \(a\).Solution. \(v=\frac{ds}{dt}=4t\Rightarrow v(3)=12~\text{m s}^{-1}\). \(a=\frac{dv}{dt}=4~\text{m s}^{-2}\). - Acceleration–Time to Velocity
An \(a\)–\(t\) graph is horizontal at \(a=3~\text{m s}^{-2}\) from \(0\) to \(5~\text{s}\). If \(u=2~\text{m s}^{-1}\), find \(v(t)\) and distance traveled.
Solution. \(v(t)=u+at=2+3t\). Distance \(=\int_{0}^{5}(2+3t)\,dt=[2t+1.5t^{2}]_{0}^{5}=47.5~\text{m}\). - Slope of \(s\)–\(t\)
Line through \((2,6~\text{m})\) and \((5,15~\text{m})\). What is the speed?
Answer. \(\text{slope}=\Delta s/\Delta t=(15-6)/(5-2)=3~\text{m s}^{-1}\). - Curved vs. Straight
Explain why a curved \(s\)–\(t\) graph always implies non-zero acceleration.
Answer. Because the slope (velocity) changes with time \(\Rightarrow \frac{d^{2}s}{dt^{2}}\neq 0\).
Section 3: Uniformly Accelerated Motion
- Uphill Skate
A skateboarder goes up a \(5~\text{m}\) slope with \(u=6~\text{m s}^{-1}\), coming to rest halfway. Find \(a\).
Solution. Over \(s=2.5~\text{m}\): \(0=u^{2}+2as\Rightarrow a=-\frac{36}{5}=-7.2~\text{m s}^{-2}\). - Downward Throw
A stone is thrown downward at \(5~\text{m s}^{-1}\) from \(20~\text{m}\). Time to hit ground?
Solution. \(s=ut+\frac12 gt^{2}\Rightarrow 20=5t+4.9t^{2}\Rightarrow t\approx 1.57~\text{s}\). - Upward Launch
A football is kicked at \(15~\text{m s}^{-1}\) upward.
a) Time to max height. b) Max height.Solution. a) \(t=\frac{u}{g}=\frac{15}{9.8}\approx 1.53~\text{s}\).
b) \(s_{\max}=\frac{u^{2}}{2g}=\frac{225}{19.6}\approx 11.48~\text{m}\). - Braking Distance
A car at \(20~\text{m s}^{-1}\) decelerates at \(4~\text{m s}^{-2}\). How far to stop?
Solution. \(0=u^{2}+2as\Rightarrow s=\frac{u^{2}}{2|a|}=\frac{400}{8}=50~\text{m}\). - Mid-race Speed
From rest, \(a=3~\text{m s}^{-2}\) for \(8~\text{s}\), then coast. Speed at \(t=8~\text{s}\)?
Answer. \(v=at=3\cdot 8=24~\text{m s}^{-1}\).
Section 4: Linear Momentum
- Crash Test
A \(1000~\text{kg}\) car at \(20~\text{m s}^{-1}\) stops in \(0.1~\text{s}\). Average force on barrier?
Solution. \(\Delta p=1000\cdot 20=2.0\times 10^{4}\). \(F_{\text{avg}}=\Delta p/\Delta t=2.0\times 10^{5}~\text{N}\). - Recoil of Gun
A \(0.01~\text{kg}\) bullet leaves a \(5~\text{kg}\) rifle at \(400~\text{m s}^{-1}\). Recoil speed?
Solution. \(0=m_R v_R+m_b v_b\Rightarrow v_R=-(0.01\cdot 400)/5=-0.8~\text{m s}^{-1}\). - Two-Mass Collision
\(m_1=2~\text{kg}\) at \(u_1=3~\text{m s}^{-1}\) hits \(m_2=1~\text{kg}\) at rest, elastically. Speeds after?
Solution.
\(v_1’=\frac{m_1-m_2}{m_1+m_2}u_1=\frac{1}{3}\cdot 3=1~\text{m s}^{-1}\).
\(v_2’=\frac{2m_1}{m_1+m_2}u_1=\frac{4}{3}\cdot 3=4~\text{m s}^{-1}\). - Inelastic Impact
A \(0.2~\text{kg}\) ball at \(5~\text{m s}^{-1}\) sticks to a \(0.8~\text{kg}\) block at rest. Final velocity?
Solution. \(v=\frac{0.2\cdot 5 + 0}{1.0}=1.0~\text{m s}^{-1}\). - Rocket Propulsion (Simplified)
A rocket ejects \(100~\text{kg}\) of gas at \(2000~\text{m s}^{-1}\). Initial mass \(1000~\text{kg}\). \(\Delta v\)?
Solution (Tsiolkovsky). \(\Delta v=v_e\ln\!\left(\frac{m_0}{m_1}\right)=2000\ln(1000/900)\approx 210.6~\text{m s}^{-1}\).
Section 5: Newton’s Laws
- Atwood Machine
\(m_1=5~\text{kg},\ m_2=3~\text{kg}\) over a frictionless pulley. Find \(a\) and \(T\).
Solution. \(a=\frac{(m_1-m_2)g}{m_1+m_2}=\frac{2\cdot 9.8}{8}=2.45~\text{m s}^{-2}\).
\(T=m_1(g-a)=5(9.8-2.45)=\mathbf{36.75~\text{N}}\). - Block on Incline with Friction
\(m=4~\text{kg},\ \theta=30^\circ,\ \mu_k=0.20\). Find \(a\) down the slope.
Solution.
\(F_{\parallel}=mg\sin\theta=4\cdot 9.8\cdot 0.5=19.6~\text{N}\).
\(f_k=\mu_k N=\mu_k mg\cos\theta=0.20\cdot 4\cdot 9.8\cdot 0.866\approx 6.79~\text{N}\).
Net \(=19.6-6.79=12.81~\text{N}\Rightarrow a=12.81/4\approx \mathbf{3.20~\text{m s}^{-2}}\). - Centripetal Force
A \(0.5~\text{kg}\) mass on a \(2~\text{m}\) string circles at \(2~\text{rev s}^{-1}\). Tension?
Solution. \(\omega=2(2\pi)=4\pi\ \text{rad s}^{-1}\).
\(F=m\omega^{2}r=0.5(4\pi)^{2}\cdot 2=16\pi^{2}\approx 158~\text{N}\). - Elevator Tension
Elevator \(m=600~\text{kg}\) accelerates upward at \(1.5~\text{m s}^{-2}\). Cable tension?
Solution. \(T-mg=ma\Rightarrow T=m(g+a)=600(9.8+1.5)=\mathbf{6780~\text{N}}\). - Forced Oscillation (Hooke + Newton)
Mass \(m=0.5~\text{kg}\) on spring \(k=100~\text{N m}^{-1}\) pulled to \(x=0.1~\text{m}\) and released. Max acceleration?
Solution. \(a_{\max}=\frac{k}{m}x=\frac{100}{0.5}\cdot 0.1=20~\text{m s}^{-2}\).
Have feedback or questions? We’d love to hear from you!
Course: Prep4Uni Physics 1
Chapter 1: Quantities and Measurement
Chapter 2: Forces and Moments
Chapter 3: Motion and Forces
Chapter 4: Energy and Fields
Chapter 5: Projectile Motion
