Topic 2: Forces and Moments
Course:
Prep4Uni Physics 1
Chapter 1: Quantities and Measurement
Chapter 2: Forces and Moments
Chapter 3: Motion and Forces
Chapter 4: Energy and Fields
Chapter 5: Projectile Motion
🚁 Overview
This topic explores how objects interact through forces and how these forces produce both linear and rotational effects. Understanding forces and moments is essential for analyzing structures, machines, and motion in physics and engineering contexts.
📖 Contents
- Types of forces
- Hooke’s Law and Elastic Forces
- Moment and torque
- Couples and the Principle of Moments
- Equilibrium Conditions
🎯 Learning Outcomes
By the end of this section, students should be able to:
- Describe forces on masses, charges, and currents in various fields
- Understand forces such as normal, frictional, buoyant, and viscous
- Apply Hooke’s Law: F = kx
- Define and apply moment of a force and torque
- Understand the concept of a couple
- Apply the principle of moments and define the
centre of gravity - Analyze equilibrium using free-body diagrams and vector methods
Table of Contents
🔢 1. Types of Forces
Contact forces (require touching):
- Normal force — acts perpendicular to the surface; balances compression (e.g., table on book).
- Friction — opposes relative motion along the surface; kinetic: \(f_k=\mu_k N\), static: \(f_s\le \mu_s N\).
- Tension — pull transmitted by an ideal (massless, inextensible) string; same magnitude along the string.
- Spring force — linear elastic restoring force: \(F=kx\) (toward equilibrium; \(k\) in N·m\(^{-1}\)).
Non-contact (field) forces (act at a distance):
- Gravitational force — attraction between masses: \(F=\;G\,\frac{m_1 m_2}{r^{2}}\) (near Earth’s surface: weight \(W=mg\)).
- Electrostatic force — between charges: \(F=\;k\,\frac{|q_1 q_2|}{r^{2}}\) (repel/attract depending on signs).
- Magnetic force — on a moving charge: \(F=q\,vB\sin\theta\) (or on a wire \(F=I L B\sin\theta\)).
- Buoyant force — upward fluid force: \(F_b=\rho g V_{\!\text{disp}}\) (Archimedes’ principle).
- Viscous/drag force — resistance in fluids; low speed: \(F\propto v\) (e.g., \(6\pi\eta r v\)); high speed: \(F\propto v^2\).
📐 Learning-Check 1
A \(2~\text{kg}\) object rests on a flat table. Identify the forces and their directions.
Answer: Weight \(W=mg\) acting downward; normal reaction \(N\) acting upward. At rest, \(N=W=2\times9.8\approx19.6~\text{N}\), so \(\sum F_y=0\).
📐 Learning-Check 2
Which of the following is a non-contact force?
A) Friction B) Tension C) Buoyant force D) Gravitational force
Answer: D) Gravitational force.
Why: It acts through a field without physical contact; the others require a surface or medium.
Tip: When drawing a free-body diagram (FBD), show each force as an arrow from the object’s centre; label magnitudes/angles and use up to two axes so you can write \(\sum F_x=0\), \(\sum F_y=0\) (and \(\sum M=0\) for rotation) clearly.
🔢 2. Hooke’s Law and Elastic Forces
Hooke’s law (linear elasticity)
- Magnitude form: \( F = k\,x \), where
\(F\) is the applied/restoring force (N), \(k\) the spring constant (N·m\(^{-1}\)), and \(x\) the extension or compression (m). - Vector/sign-convention form: the spring’s restoring force opposes the displacement:
\( \vec{F}_{\text{spring}} = -\,k\,\vec{x} \). - Elastic potential energy stored in the spring:
\( U(x)=\frac12\,k\,x^{2} \) (J).
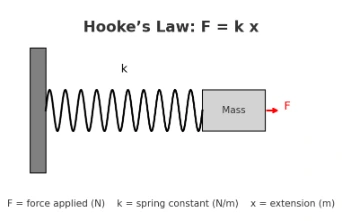
Static equilibrium with weight: If a mass \(m\) hangs from a vertical spring and comes to rest after stretching by \(x\),
then \( \sum F_y=0 \Rightarrow kx = mg \Rightarrow x=\frac{mg}{k} \).
Series/parallel springs (effective stiffness)
- Series: \( \displaystyle \frac{1}{k_{\mathrm{eq}}}=\frac{1}{k_1}+\frac{1}{k_2}\;\Rightarrow\;
k_{\mathrm{eq}}=\frac{k_1 k_2}{k_1+k_2} \). - Parallel: \( k_{\mathrm{eq}}=k_1+k_2 \).
Graph method (lab tip): Plot applied force \(F\) (y-axis) vs extension \(x\) (x-axis). The best-fit straight line
has slope \(k\) (units N·m\(^{-1}\)). The linear region ends near the elastic limit.
Worked example
A spring stretches \(4~\text{cm}=0.04~\text{m}\) under a \(2~\text{N}\) load. Find \(k\).
Using \( F=kx \Rightarrow k=\frac{F}{x}=\frac{2}{0.04}= \mathbf{50}~\text{N·m}^{-1}. \)
📐 Learning-Check 1
A spring extends \(0.08~\text{m}\) when a \(4~\text{N}\) force is applied. What is \(k\)?
Solution:
\( k=\frac{F}{x}=\frac{4}{0.08}= \mathbf{50}~\text{N·m}^{-1}. \)
📐 Learning-Check 2
True or False: Hooke’s law holds for any deformation, even if the spring is permanently stretched.
Answer: False.
Hooke’s law applies only within the elastic limit. Beyond yield, the \(F\)–\(x\) relation is no longer linear and permanent deformation can occur.
Common pitfalls: (i) forgetting to convert cm to m; (ii) using \(F= kx\) with the wrong sign when writing vector equilibrium;
(iii) assuming linear behavior beyond the elastic limit; (iv) mixing weight \(W=mg\) with mass \(m\) (units!).
🔢3. Moment and Torque
What is a moment? The moment of a force (turning effect) about a pivot measures how strongly the force tends to rotate an object.- Scalar (perpendicular) definition: For a force applied perpendicularly at a distance r from the pivot, \( \;M = F\,r\; \) with SI unit N·m.
- General (angled) case: When the force makes an angle \( \theta \) to the lever arm, \[ M = F\,r\,\sin\theta \quad\text{or}\quad M = F_\perp\,r, \] where \( F_\perp = F\sin\theta \) is the component of the force perpendicular to the lever arm.
- Vector definition (torque): \( \vec{\tau} = \vec{r} \times \vec{F} \); \( \|\vec{\tau}\| = r\,F\,\sin\theta \). Direction given by the right-hand rule (thumb = \( \vec{\tau} \), fingers curl from \( \vec{r} \) to \( \vec{F} \)).
- Units: Newton–metre (N·m). Moments/torques are not “joules” even though \(1~\text{N·m} = 1~\text{J}\) dimensionally; energy is a scalar work quantity, torque is an axial (pseudovector) quantity.
- Sign convention: In 2D statics, take counter-clockwise positive (CCW \(+\)), clockwise negative (CW \(−\)). Be consistent across the page.
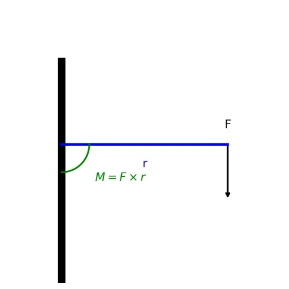
📐 Learning-Check 1 (moment magnitude): A \(12~\text{N}\) force is applied at a perpendicular distance \(0.25~\text{m}\) from a pivot. Compute \(M\). \[ M = F\,r = 12 \times 0.25 = \mathbf{3.0}~\text{N·m}. \]
📐 Learning-Check 2 (lever arm from torque): A spanner applies a torque of \(10~\text{N·m}\). If the applied force is \(20~\text{N}\), find the perpendicular distance \(d\). \[ \tau = F\,d \;\Rightarrow\; d = \frac{\tau}{F} = \frac{10}{20} = \mathbf{0.50}~\text{m}. \]
SEO note for learners: Engineers often search “moment vs torque,” “lever arm,” and “right-hand rule.” Remember: moment is the turning effect; torque is the vector form \( \boldsymbol{\tau} = \boldsymbol{r} \times \boldsymbol{F} \); use \(M = F\,r\,\sin\theta\) for angled forces, and N·m as the SI unit.🔢4. Couples and the Principle of Moments
Couple:- Two equal and opposite forces acting on different lines.
- Produces pure rotation (no net force, only turning effect).
- For an object in rotational equilibrium: Sum of clockwise moments = Sum of anticlockwise moments
- The picture below illustrates the moment due to two equal forces F acting at distance D apart but in opposite directions, forming a rotating moment called a pure couple.
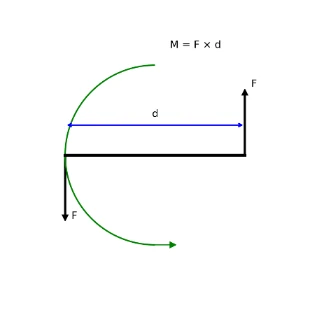
📐Learning-Check 1: Two equal and opposite forces of 15 N act on a steering wheel, 0.4 m apart. What is the moment (torque) produced by this couple?
Solution: Moment of a couple = One force × Distance between forces = 15 N × 0.4 m = 6 Nm
📐Learning-Check 2: A plank is balanced on a pivot. A 30 N weight is placed 1.2 m from the pivot. What weight must be placed 0.8 m on the other side to balance the plank?
Solution: Clockwise moment = 30 N × 1.2 m = 36 Nm To balance: Anticlockwise moment = W × 0.8 m → W = 36 / 0.8 = 45 N
🔢5. Equilibrium Conditions
Translational Equilibrium (no net force):
- Object remains at rest or moves with constant velocity (Newton’s First Law).
- In 2D:
\( \sum F_x = 0,\quad \sum F_y = 0. \) - In 3D, also \( \sum F_z = 0 \).
Rotational Equilibrium (no net moment/torque):
- No angular acceleration; object does not start/stop spinning.
- About any chosen pivot:
\( \sum M = 0. \)
Free-Body Diagrams (FBDs):
- Show the body as a simple shape (point/box/beam) and draw all external forces acting on it (no internal forces between parts of the same rigid body).
- Label magnitudes and directions; choose and mark a sign convention for moments (e.g., counter-clockwise \(+\)).

- Friction models (useful in FBDs):
- Static friction (no slip): \( |f| \le \mu_s N \) (at impending motion: \( f=\mu_s N \)).
- Kinetic friction (sliding): \( f_k = \mu_k N \) opposing motion.
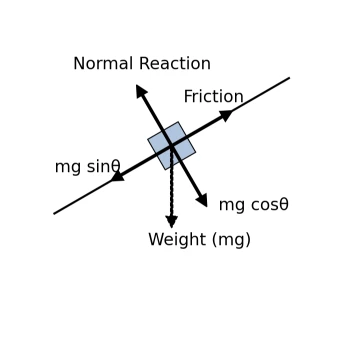
Inclined Plane Decomposition (angle \( \theta \) to horizontal):
- Weight: \( mg \) acts vertically downward.
- Components along/normal to plane:
\( \;mg\sin\theta \) (down the plane), \( mg\cos\theta \) (into the plane). - Normal reaction (no lift-off): \( N = mg\cos\theta \) (if no other vertical forces).
- If at rest (no slip): \( \sum F_{\parallel}=0 \Rightarrow f = mg\sin\theta \) with \( |f|\le \mu_s N \).
Beam Equilibrium (supports & moments):
A beam is in equilibrium when both translation and rotation balance:
\( \sum F_x=0,\; \sum F_y=0,\; \sum M=0 \).
For a simply supported beam with reactions \(R_A, R_B\), and a point load \(P\) at distance \(a\) from support \(A\):
Choose moments about \(A\):
\( \sum M_A = 0 \Rightarrow R_B L – P a = 0 \Rightarrow R_B = \frac{P a}{L}. \)
Then vertical forces:
\( \sum F_y = 0 \Rightarrow R_A + R_B – P = 0 \Rightarrow R_A = P – \frac{P a}{L} = P\!\left(1-\frac{a}{L}\right). \)

Worked Example (Ladder idea, FBD thinking)
A ladder leans against a rough wall and rests on a rough floor. Draw the FBD: weight \(mg\) at the ladder’s centre, normal reactions at wall and floor, and friction forces at both contacts opposing possible slip. Apply
\( \sum F_x=0,\; \sum F_y=0,\; \sum M=0 \)
about a convenient pivot (often the floor contact) to find unknown reactions. Check that any friction forces obey \( |f|\le \mu N \).
📐Learning-Check 1:
Draw an FBD for a box pushed across a rough floor at constant speed. Label all forces and write the equilibrium equations.
Answer (sketch & equations):
Forces: applied \(F\) (forward), friction \(f_k\) (back), weight \(mg\) (down), normal \(N\) (up). Since speed is constant:
\( \sum F_x=0 \Rightarrow F – f_k=0,\;
\sum F_y=0 \Rightarrow N – mg = 0,\;
f_k=\mu_k N. \)
📐Learning-Check 2:
A beam is in static equilibrium. Which must be true?
A) \( \sum F \ne 0 \) and \( \sum M = 0 \)
B) \( \sum F = 0 \) and \( \sum M = 0 \)
C) \( \sum F = 0 \) and \( \sum M \ne 0 \)
D) \( \sum F \ne 0 \) and \( \sum M \ne 0 \)
Answer: B) \( \sum F = 0 \) and \( \sum M = 0 \).
Explanation: Complete (static) equilibrium requires zero net force and zero net moment.
💡Some Interesting Examples
- \(A = 80~\text{N}\) directed horizontally to the right,
- \(B = 60~\text{N}\) directed vertically upward.
Section 1 — Graphical (tip-to-tail) vector addition
- From O, draw vector \( \vec A \) to the right (length ∝ 80 N).
- From the tip of \( \vec A \), draw vector \( \vec B \) upward (length ∝ 60 N).
- The closing vector from the tip of \( \vec B \) back to O is the reaction \( \vec R \), satisfying \( \vec A + \vec B + \vec R = \vec 0 \Rightarrow \vec R = -(\vec A + \vec B)\).
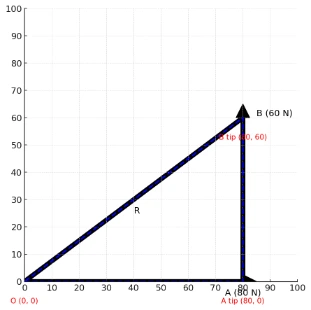
Vector addition (tip-to-tail): the reaction is equal in magnitude and opposite in direction to the resultant.
Section 2 — Resolved-component (analytic) method
- Resolve forces into Cartesian components (take \(+x\) to the right, \(+y\) upward): \[ \vec A = (80,\,0)\ \text{N},\qquad \vec B = (0,\,60)\ \text{N}. \]
- Resultant that must be opposed: \[ \vec A + \vec B = (80,\,60)\ \text{N} \quad\Rightarrow\quad \vec R = -(\vec A+\vec B) = (-80,\,-60)\ \text{N}. \]
- Magnitude of the reaction: \[ |\vec R| = \sqrt{(-80)^{2}+(-60)^{2}} = \sqrt{6400+3600} = \sqrt{10000} = 100~\text{N}. \]
- Direction of the reaction (angle from the \(+x\) axis): \[ \theta_R = \tan^{-1}\!\left(\frac{R_y}{R_x}\right) = \tan^{-1}\!\left(\frac{-60}{-80}\right). \] Since \(R_x<0\) and \(R_y<0\), \(\vec R\) lies in the third quadrant, so add \(180^\circ\): \[ \theta_R = 180^\circ + \tan^{-1}\!\left(\frac{60}{80}\right) \approx 180^\circ + 36.87^\circ = 216.87^\circ. \] (Equivalently: \(36.87^\circ\) below the \(-x\) direction.)
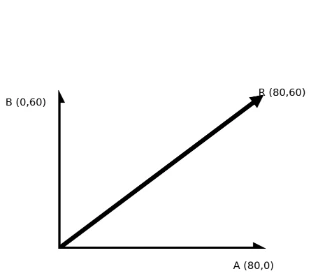
Component method: sum components, then use \( |\vec R|=\sqrt{R_x^2+R_y^2} \) and \( \theta_R=\tan^{-1}(R_y/R_x) \) with the correct quadrant.
Example 2: Centre of Gravity (Barycentre) of the Sun–Earth–Moon System
Problem. Three bodies lie (approximately) on a line:
- Sun: mass \(M_{\odot}=1.989\times 10^{30}\,\text{kg}\) at \(x_{\odot}=0\).
- Earth: mass \(M_E=5.972\times 10^{24}\,\text{kg}\) at \(x_E=1\,\text{AU}=1.496\times 10^{11}\,\text{m}\).
- Moon: mass \(M_m=7.347\times 10^{22}\,\text{kg}\) at \(x_m=1.496\times 10^{11}+3.84\times 10^{8}=1.49984\times 10^{11}\,\text{m}\).
Method (1D barycentre): The centre of gravity along this line is
\[ x_{\text{CG}}=\frac{\sum_i M_i x_i}{\sum_i M_i}. \]
- Total mass.
\[ M_{\text{tot}}=M_{\odot}+M_E+M_m =1.989006045\times 10^{30}\,\text{kg}\quad(\text{to }7\ \text{sig. figs.}) \]
- Weighted sum of positions.
\[ \sum_i M_i x_i =M_{\odot}x_{\odot}+M_E x_E+M_m x_m =0+(5.972\times 10^{24})(1.496\times 10^{11}) +(7.347\times 10^{22})(1.49984\times 10^{11}). \] \[ \sum_i M_i x_i \approx 9.044305245\times 10^{35}\ \text{kg·m}. \]
- Centre of gravity.
\[ x_{\text{CG}} =\frac{9.044305245\times 10^{35}}{1.989006045\times 10^{30}} \ \text{m} \approx 4.547\times 10^{5}\ \text{m}. \]
Answer. \(\displaystyle x_{\text{CG}}\approx 4.55\times 10^{5}\ \text{m}\) from the Sun’s centre (about \(4.55\times 10^{5}\,\text{m} = 455\,\text{km}\) along the Sun–Earth line). This lies deep inside the Sun (solar radius \(\sim 6.96\times 10^{8}\,\text{m}\)).
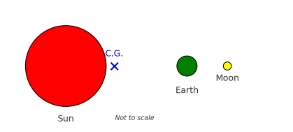
Notes for students (accuracy & modelling):
- This is a collinear approximation. In reality the bodies move in 3D; the true instantaneous barycentre is still given by the same mass-weighted sum in vector form.
- The Sun’s dominance (\(M_{\odot}\gg M_E\gg M_m\)) keeps the barycentre well inside the Sun; adding the Moon shifts it only slightly from the Sun–Earth two-body value.
- For vectors in 3D, replace \(x_i\) with \(\vec r_i\): \(\displaystyle \vec r_{\text{CG}}=\frac{\sum_i M_i \vec r_i}{\sum_i M_i}\).
Also called: barycentre, mass centre of a multi-body system. Key idea: mass-weighted average of positions.
Example 3: Maximum Incline Before Sliding
Problem. A box of mass \(m=10~\text{kg}\) rests on a rough plane. The coefficient of static friction is \(\mu=0.20\). What is the largest angle \(\theta_{\max}\) (measured from the horizontal) for which the box does not start sliding?

- Resolve forces.
Take the plane angle as \(\theta\) to the horizontal. Then the weight components relative to the plane are: \[ W_{\parallel}=mg\sin\theta,\qquad W_{\perp}=mg\cos\theta, \] and the normal reaction is \[ N=W_{\perp}=mg\cos\theta. \] At impending motion (just about to slip up or down the plane), the maximum static friction is \[ f_{\max}=\mu N=\mu\,mg\cos\theta. \]
- Limiting equilibrium at the threshold of sliding.
For a box on the verge of sliding down, friction acts up the plane with magnitude \(f_{\max}\). Balance along the plane: \[ \underbrace{mg\sin\theta}_{\text{down-plane}}=\underbrace{f_{\max}}_{\text{up-plane}}=\mu\,mg\cos\theta. \]
- Solve for \(\theta_{\max}\).
Cancel \(mg>0\) and divide by \(\cos\theta\): \[ \tan\theta_{\max}=\mu \quad\Longrightarrow\quad \theta_{\max}=\arctan(\mu)=\arctan(0.20)\approx 11.31^{\circ}. \]
Answer. \(\displaystyle \theta_{\max}\approx 11.3^{\circ}\).
Why mass cancels. The result depends only on the friction coefficient and the plane angle because both driving (\(mg\sin\theta\)) and resisting (\(\mu mg\cos\theta\)) terms are proportional to \(m\).
Static vs kinetic friction. This \(\theta_{\max}\) uses static friction \(\mu\). Once sliding begins, the coefficient drops to the kinetic value \(\mu_k\) (typically \(\mu_k<\mu\)), so the required angle to keep sliding can be smaller.
Direction check. For an up-slope impending motion (you push uphill), the balance becomes \(mg\sin\theta+\text{(applied up-slope shortfall)}=\mu mg\cos\theta\); the limiting angle relation \(\tan\theta_{\max}=\mu\) still marks the onset of unavoidable down-slope slip when no extra force is applied.
⚙️Key Concepts Recap
| Concept | Formula | Notes |
|---|---|---|
| Hooke’s Law | \( F = k\,x \) | Linear spring (within elastic limit); \(F\) in newtons, \(k\) in N·m\(^{-1}\), \(x\) in m. |
| Moment (scalar) | \( M = F\,d_\perp \) | \(d_\perp\): perpendicular distance to pivot; units N·m. |
| Torque (vector) | \( \vec{\tau} = \vec{r}\times \vec{F},\quad |\vec{\tau}| = r\,F\sin\theta \) | Direction by right-hand rule; reduces to moment magnitude for planar problems. |
| Static Equilibrium | \( \sum F_x=0,\ \sum F_y=0,\ \sum M=0 \) | No linear or angular acceleration (object at rest or constant velocity with no rotation). |
Proceed to: Topic 3: Motion and Forces
Go back to Prep4Uni Physics 1
Additional Resources:
📝 EXERCISES
Forces and Moments: Questions & Answers
1. Types of Forces
Q1: A block rests on an inclined plane at 30°. List all the forces acting on it, describe their directions, and explain how each arises.
A1:
- Weight \((mg)\): acts vertically downward (gravitational attraction of Earth).
- Normal reaction \((N)\): acts perpendicular to the plane (contact force preventing interpenetration).
- Friction \((f)\): acts along the plane opposing impending or actual motion.
- Static regime: \( f \le \mu_s N \) (at rest or just about to move).
- Kinetic regime: \( f = \mu_k N \) (sliding).
- If attached — Tension \((T)\): along the rope/cable, pulling on the block.
Q2: Explain the difference between viscous drag and buoyant force, including their origins and how they scale with velocity or volume.
A2:
- Viscous drag (fluid resistance): due to shear in a viscous fluid. For a small sphere in laminar flow (low Reynolds number),
\( F_d = 6\pi \eta r v \) — drag grows linearly with speed \(v\), with viscosity \(\eta\) and radius \(r\). - Buoyant force (Archimedes): due to vertical pressure gradient in a fluid,
\( F_b = \rho_{\text{fluid}} g V \) — depends on displaced volume \(V\), independent of speed (quasi-static).
Q3: A small metal bead is suspended from a thread (gravity only), then charged and placed in a uniform electric field. Identify the forces in each case and how tension changes.
A3:
- Gravity only: weight \(mg\) downward; tension \(T\) upward with \(T=mg\) at rest.
- With uniform field: add electrostatic force \(F_e = qE\) (direction set by the field and sign of \(q\)).
At rest: \(T = mg \mp qE\) (minus if \(qE\) upward, plus if downward).
Q4: Compare contact vs non-contact forces with engineering examples where each dominates.
A4:
- Contact: brake pads on a rotor (frictional torque); geared transmissions (normal forces between teeth).
- Non-contact: aerodynamic lift on a wing (pressure field); magnetic levitation (magnetic forces on conductors/magnets).
Q5: Derive the net horizontal force on a body in a viscous fluid with an applied force, and state the terminal-velocity condition (laminar case).
A5:
- Equation of motion (1D): \( m a = F_{\text{applied}} – F_d \), with laminar drag \( F_d = 6\pi \eta r v \).
- Hence \( m \,\frac{dv}{dt} = F_{\text{applied}} – 6\pi \eta r v \).
- Terminal velocity (steady state \(a=0\)): \( v_t = \frac{F_{\text{applied}}}{6\pi \eta r} \).
For a falling sphere with weight minus buoyancy as the driving force, replace \(F_{\text{applied}}\) accordingly.
Forces and Moments: Problems & Solutions
1. Types of Forces
Problem 1: A 5 kg block lies on a horizontal table. List all forces acting on it and compute the normal force.
Solution:
Forces: weight (mg = 5×9.81 = 49.05 N down), normal force N upward. Equilibrium ⇒ N = 49.05 N.
Problem 2: A sphere of radius 0.1 m moves at 0.5 m/s through oil (η = 0.2 Pa·s). Calculate the viscous drag.
Solution:
Stokes’ law: Fd = 6π η r v = 6π×0.2×0.1×0.5 ≈ 0.188 N.
Problem 3: A 2 kg bead on a string is in equilibrium in a downward electric field of 400 N/C. What charge must the bead carry?
Solution:
Equilibrium: qE = mg ⇒ q = (2×9.81)/400 ≈ 0.0491 C.
Problem 4: Compare the magnitudes of the gravitational force and electrostatic force between two protons separated by 1 fm.
Solution:
Fg ≈ 1.86×10⁻³⁵ N; Fe ≈ 2.30×10⁻⁸ N.
Problem 5: A body experiences an applied force of 10 N and a drag force Fd = 2v (in N). Determine the terminal velocity.
Solution:
At terminal velocity: 10 = 2v ⇒ v = 5 m/s.
2. Hooke’s Law and Elastic Forces
Problem 6: A spring extends by 0.04 m under a 2 N load. Find the spring constant k.
Solution:
k = F/x = 2 / 0.04 = 50 N/m.
Problem 7: Two springs (k₁ = 100 N/m, k₂ = 200 N/m) are connected in series. Find the equivalent k.
Solution:
1/kₛ = 1/100 + 1/200 = 0.015 ⇒ kₛ ≈ 66.7 N/m.
Problem 8: A mass m = 0.5 kg on a spring (k = 80 N/m) is released from rest at x = 0.1 m. Find maximum speed.
Solution:
½k x² = ½m v² ⇒ v = x√(k/m) = 0.1√(80/0.5) ≈ 1.26 m/s.
Problem 9: Two identical springs (k = 120 N/m) in parallel support a 240 N weight. Find the extension.
Solution:
kₚ = 2k = 240 N/m ⇒ x = F/kₚ = 240/240 = 1.0 m.
Problem 10: A mass-spring system oscillates with period T = 0.5 s and m = 0.2 kg. Find k.
Solution:
T = 2π√(m/k) ⇒ k = 4π²m/T² ≈ 31.6 N/m.
3. Moment and Torque
Problem 11: A 30 N force is applied perpendicular to a lever arm 0.3 m from the pivot. Calculate the moment.
Solution:
M = F·d = 30×0.3 = 9 N·m.
Problem 12: A wrench 0.25 m long is used at 60°. What moment results from a 40 N force?
Solution:
M = F·r·sinθ = 40×0.25×sin60° ≈ 8.66 N·m.
Problem 13: A door 0.8 m wide needs 20 N at 30° to open with torque 12 N·m. Verify whether 20 N is sufficient.
Solution:
Effective arm = 0.8 sin30° = 0.4 m ⇒ M = 20×0.4 = 8 N·m (insufficient).
Problem 14: A torque of 15 N·m is required. What force at 0.2 m perpendicular arm?
Solution:
F = M/d = 15/0.2 = 75 N.
Problem 15: Two forces of 25 N produce a net moment of 7.5 N·m on opposite sides of a pivot. Find their separation.
Solution:
d = M/F = 7.5/25 = 0.3 m.
4. Couples and the Principle of Moments
Problem 16: Two 15 N forces act opposite, 0.4 m apart. Calculate the couple’s moment.
Solution:
τ = F·d = 15×0.4 = 6 N·m.
Problem 17: A seesaw of length 4 m carries a 30 kg child at 1 m from pivot. What mass balances at 1.5 m?
Solution:
m₂ = (30×1)/1.5 = 20 kg.
Problem 18: A uniform beam weight 100 N is pivoted at center. Two opposite 60 N forces act at ends. Determine net moment.
Solution:
Net force = 0; couple moment = 60×(L/2)+60×(L/2) = 60L (pure couple).
Problem 19: Show with numbers why a couple’s moment is independent of reference point.
Solution:
Changing pivot shifts lever arms equally for both forces; net M = F·d remains unchanged.
Problem 20: A wrench applies +20 N and –20 N at ends 0.5 m apart. Calculate total moment about midpoint.
Solution:
τ = 20×0.5 = 10 N·m.
5. Equilibrium Conditions
Problem 21: A block is pulled at constant speed by 50 N on a rough floor (μ=0.3). Find frictional force.
Solution:
N = mg = 49.05 N; f = μN = 0.3×49.05 = 14.72 N (so applied force must balance 14.72 N to maintain constant speed).
Problem 22: A ladder 5 m long leans at 60°; weight 600 N at midpoint. Find minimum μ at base to prevent slipping.
Solution:
Rw = (600×2.5×cos60°)/(5×sin60°) ≈ 173.2 N; N = 600 N; μ = 173.2/600 ≈ 0.29.
Problem 23: A simply supported beam 6 m long carries 800 N at 2 m from A. Find reactions at A and B.
Solution:
RB·6 = 800·2 ⇒ RB = 266.7 N; RA = 800 − 266.7 = 533.3 N.
Problem 24: A plank 3 m long, weight 200 N, has loads 150 N at 0.5 m and 100 N at 2 m from left support. Find support forces.
Solution:
ΣMA: RB·3 = 150·0.5 + 100·2 = 75 + 200 = 275 ⇒ RB = 91.7 N; RA = 200+150+100 − 91.7 = 358.3 N.
Problem 25: A beam hinged at A and roller at B supports loads 300 N at 1 m and 200 N at 3 m along a 5 m beam. Find reactions at A and B.
Solution:
ΣMA: RB·5 = 300·1 + 200·3 = 300 + 600 = 900 ⇒ RB = 180 N; ΣFy: RA + RB = 500 ⇒ RA = 320 N.
Have feedback or questions? We’d love to hear from you!
Chapter 1: Quantities and Measurement
Chapter 2: Forces and Moments
Chapter 3: Motion and Forces
Chapter 4: Energy and Fields
Chapter 5: Projectile Motion
