Energy and Fields

Topic 4: Energy and Fields

Chapter 1: Quantities and Measurement
Chapter 2: Forces and Moments
Chapter 3: Motion and Forces
Chapter 4: Energy and Fields
Chapter 5: Projectile Motion

🚁Overview

This topic introduces the principles of energy, work, and power, along with the concepts of gravitational and electric fields. These ideas help us understand how forces can transfer energy, store it in various forms, and influence the motion of particles over a distance.

📖Contents

Energy types and transfer
Work, kinetic and potential energy
Fields and Field Lines
Equipotentials and Work in Fields
Power and efficiency

🎯Learning Outcomes

By the end of this section, students should be able to:

Identify energy stores and describe energy transfers
Apply the principle of conservation of energy
Define and calculate work, kinetic energy, and potential energy
Understand gravitational and electric fields and interpret field lines
Use equipotential concepts and relate work to potential energy changes
Calculate power and efficiency and apply these ideas to real-world devices

🔢1. Energy Types and Transfers

The total energy of an isolated system stays constant. Energy can be stored in different forms and transferred from one system to another, but it is never created or destroyed.

Main energy stores (with quick cues).

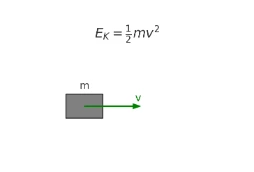
Kinetic — motion; \(E_k=\frac12 m v^{2}\).
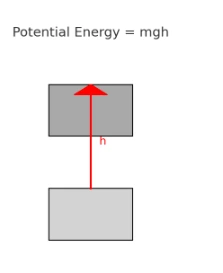
Gravitational potential — height in a field; \(E_g=mgh\).
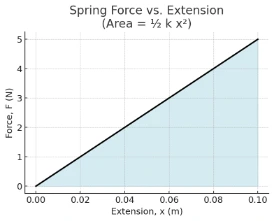
Elastic (strain) — deformation; \(E_e=\frac12 k x^{2}\).
Chemical — bonds (fuels, food, batteries).
Thermal — temperature/random motion; \( \Delta E = m c\,\Delta T \).
Electrical — separated charges / current in circuits.
Nuclear — binding energy; \(E=\Delta m\,c^{2}\).

Energy transfers.

By mechanical work (forces doing work), e.g. \(W=F s\).
By electrical work, e.g. \(W=V I t\).
By heating (conduction, convection, radiation).
By waves (e.g., light, sound).

Conservation of energy.

Energy cannot be created or destroyed — only transferred or transformed.

Examples of energy transfer.

Falling object: gravitational potential → kinetic (ignore air resistance).
Rubber band: elastic → kinetic.
Battery torch: chemical → electrical work → light + thermal.
Kettle: electrical → heating → thermal energy of water.
Speaker: electrical → sound waves → kinetic/thermal of air.

📐 Learning-Check 1

Q: Name two ways energy can be transferred from one system to another.
A: By mechanical work and by heating.

📐 Learning-Check 2

Q: What type of energy store increases when a spring is compressed?
A: Elastic potential energy.

🔢2. Work, Kinetic Energy, and Potential Energy (unit: joule, J)

Work done (W): W = F × d. The figure shows a block pushed by a force F through a displacement d.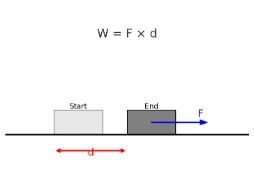

Block pushed along a horizontal surface: force F acts in the same direction as displacement d. — Work: W = F × d

Kinetic energy (KE): KE = ½mv².

A mass m moving with velocity v. — Moving mass: KE = ½mv²

Elastic potential energy (EPE): EPE = ½kx². For a spring obeying Hooke’s law (F = kx), the shaded triangular area under the F–x graph equals the stored elastic energy.

Force–extension graph of a spring; triangular area under the straight line equals elastic potential energy. — Elastic energy from force–extension graph: ½kx²

Gravitational potential energy (GPE): GPE = mgh (or ΔE_p = mgΔh).

Raising a block through height h increases gravitational potential energy mgh. — Raise by height h: *GPE* = *mgh*

Worked examples

Work: A 10 N force moves an object 4 m. W=10×4=40 J.
Kinetic energy: 2 kg at 3 m/s: KE=½×2×3²=9 J.
Elastic energy: k=200 N/m, x=0.1 m: EPE=½×200×(0.1)²=1 J.
Gravitational energy: 5 kg lifted 3 m: GPE=5×9.8×3=147 J.

📐 Learning-Check 1.

Q: A 10 N force moves an object 4 m in the direction of the force. How much work is done?

A: W = F d = 10 × 4 = 40 J.

📐 Learning-Check 2.

Q: What is the kinetic energy of a 0.5 kg ball moving at 6 m/s?

A: KE = ½mv² = 0.5 × 0.5 × 36 = 9 J.

🔢3. Fields and Field Lines

Gravitational field. A region in which a mass experiences a gravitational force.

Field strength: \( g=\frac{F}{m} \) (near Earth, \( g\approx 9.8~\text{m s}^{-2} \), directed toward Earth’s centre).
Field lines: point toward the centre of mass; lines never cross.

Gravitational field lines pointing radially inward toward Earth. Field strength g = F/m. — Gravitational field: lines are radial and inward.

Electric field. A region in which a charge experiences an electric force.

Field strength: \( E=\frac{F}{q} \).
Direction: lines start on \(+\) charges and end on \( – \); they point away from \(+\) and toward \( – \).
Uniform field (parallel plates): approximately \( E=\frac{V}{d} \) — straight, parallel, equally spaced lines.

Electric field diagram: lines leaving positive charges and entering negative charges; uniform between parallel plates. — Electric field patterns and a uniform field between parallel plates.

What field lines show.

Direction of the force on a small test mass/charge placed at that point.
Strength — denser (closer) lines indicate a stronger field.
In electrostatics, lines meet conducting surfaces at right angles; lines do not intersect.

📐 Learning-Check 1. In a gravitational field, in what direction do the field lines point?

A: Toward the mass (e.g., toward Earth’s centre).

📐 Learning-Check 2. Are electric field lines closer together in strong or weak fields?

A: Closer together in stronger fields (larger \(E\)).

🔢4. Equipotentials and Work in Fields

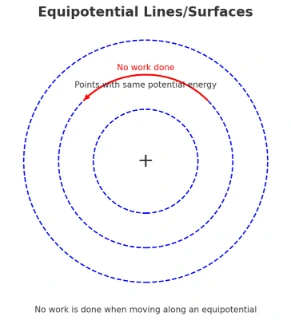
Equipotential lines/surfaces. Sets of points that share the same potential (\(V\) for electric fields; potential energy per unit charge/mass). Moving along an equipotential does no work:

\( \Delta W = 0 \) and \( \Delta V = 0 \) along an equipotential.
Equipotentials are always perpendicular to field lines.
Closer spacing of equipotentials ⇒ stronger field (larger gradient).

Equipotential lines drawn perpendicular to field lines — Equipotentials: equal potential everywhere along a line/curve.

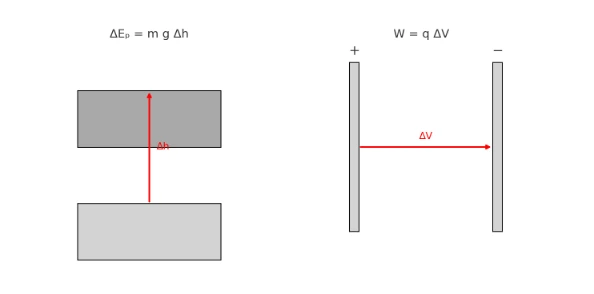
Work and potential energy.

Gravitational: \( \Delta E_p = m g\,\Delta h \). If the object moves down (\(\Delta h<0\)), gravitational potential energy decreases and the same amount can appear as kinetic energy (neglecting losses).
Electric: \( W = q\,\Delta V \). For a uniform field between plates, \( \Delta V = E d \) and \( W = q E d \).

Work from potential difference and the relation between E, d, and ΔV — Work from potential differences: \(W=q\,\Delta V\); in a uniform field, \(\Delta V = E d\).

Worked example. A \(2~\text{kg}\) mass descends \(5~\text{m}\).

\( \Delta E_p = m g\,\Delta h = 2 \times 9.8 \times 5 = 98~\text{J} \). This \(98~\text{J}\) is released (e.g., as kinetic energy) if non-conservative losses are negligible.

📐 Learning-Check 1. True or False: Work is done when a charge moves along an equipotential line.

A: False. Along an equipotential, \( \Delta V = 0 \Rightarrow W = q\,\Delta V = 0 \).

📐 Learning-Check 2. A \(3~\text{C}\) charge moves through a potential difference of \(12~\text{V}\). How much work is done?

A: \( W = q\,\Delta V = 3 \times 12 = \mathbf{36~J} \).

🔢5. Power and Efficiency

Power, \(P\) — rate of doing work / transferring energy.

\( P = \frac{W}{t} = \frac{\Delta E}{t} \) (unit: watt, W = J·s\(^{-1}\)).
For constant speed in a straight line: \( P = F\,v \).

Efficiency — fraction of input energy (or power) that becomes useful output.

\( \text{Efficiency} = \frac{\text{useful output}}{\text{total input}} \times 100\% \).
Equivalently with power: \( \text{Efficiency} = \frac{P_{\text{useful}}}{P_{\text{in}}} \times 100\% \).

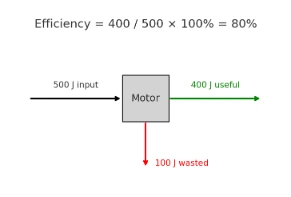
Energy flow diagram for a motor showing useful output versus wasted energy — Energy flow: only part of the input becomes useful output; the rest is dissipated (e.g., heat, sound).

Worked example. A motor delivers \(400~\text{J}\) of useful energy from \(500~\text{J}\) input.

Efficiency: \( \text{Efficiency} = \frac{400}{500}\times 100\% = \mathbf{80\%} \).

📐 Learning-Check 1. A 60 W bulb operates for 10 s. How much energy does it use?

A: \( E = P\,t = 60 \times 10 = \mathbf{600~\text{J}} \).

📐 Learning-Check 2. A machine uses \(1000~\text{J}\) of energy but delivers \(300~\text{J}\) of useful work. What is its efficiency?

A: \( \frac{300}{1000}\times 100\% = \mathbf{30\%} \).

⚙️Key Concepts Recap

Concept	Formula	Notes
Work	\( W = Fd\cos\theta \)	\(\theta\) is angle between force and displacement
Kinetic energy	\( KE = \frac12 m v^2 \)	Always positive
Gravitational potential	\( GPE = m g h \)	Relative to a reference height
Power	\( P = \frac{W}{t} \) or \( P = Fv \)	Rate of doing work
Efficiency	\( \frac{\text{useful}}{\text{total}} \times 100\% \)	Expressed as a percentage

Proceed to: Topic 5: Projectile Motion

Go back to Prep4Uni Physics 1

Additional Resources:

To deepen your understanding, you are strongly encouraged to explore the materials provided on the following pages.

Classical Mechanics
Dynamics and Kinematics
Newton’s First Law of Motion

Newton’s Second Law of Motion

Newton’s Third Law of Motion
Fundamental Forces of Nature
Kinematics
Statics
Solid Mechanics

📝EXERCISES

25 Learning-Check Questions & Answers

Section 1: Energy Stores & Transfers

Q: What is meant by an energy “store”?
A: A way energy is held in a system (e.g., chemical, thermal, gravitational).
Q: Give two examples of energy-transfer mechanisms.
A: Mechanical work (force × distance) and heating (conduction/convection/radiation).
Q: State the principle of conservation of energy.
A: Energy cannot be created or destroyed—only transferred or transformed.
Q: In a swinging pendulum, which stores interchange?
A: Gravitational potential ↔ kinetic.
Q: Distinguish an open system from a closed system in energy terms.
A: Open: exchanges energy with surroundings; Closed: does not.

Section 2: Work & Kinetic Energy

Q: Define “work done” by a force.
A: \( W = F\,s\cos\theta \) (in the force direction).
Q: What is the SI unit of work and energy?
A: Joule (J).
Q: Write the formula for kinetic energy.
A: \( KE = \frac12 m v^{2} \).
Q: State the work–energy theorem.
A: Net work done equals the change in kinetic energy.
Q: A \(2~\text{kg}\) mass accelerates from rest to \(5~\text{m s}^{-1}\). Find \(KE\).
A: \( KE = \frac12(2)(5^{2}) = 25~\text{J} \).

Section 3: Potential Energy & Equipotentials

Q: Define gravitational potential energy near Earth’s surface.
A: \( \Delta E_{p} = m g\,\Delta h \).
Q: What is an equipotential surface?
A: A surface with equal potential everywhere—no work moving along it.
Q: How is work related to change in potential energy?
A: \( W = -\,\Delta E_{p} \) (work by the field reduces \(E_p\)).
Q: Write the expression for elastic potential energy in a spring.
A: \( E_{\text{elastic}}=\frac12 k x^{2} \).
Q: A \(1~\text{kg}\) object is lifted \(3~\text{m}\). What \( \Delta E_p \) does it gain?
A: \( 1\times 9.8\times 3 = 29.4~\text{J} \).

Section 4: Fields (Gravitational & Electric)

Q: Define gravitational field strength \( g \).
A: \( g=\frac{F}{m} \) on a small test mass (N kg\(^{-1}\)).
Q: State Newton’s law of gravitation.
A: \( F=G\frac{m_1 m_2}{r^{2}} \).
Q: Define electric field strength \( E \).
A: \( E=\frac{F}{q} \) on a positive test charge (N C\(^{-1}\)).
Q: How do field lines represent field strength?
A: Denser lines ⇢ stronger field.
Q: Two \(1~\mu\text{C}\) charges \(0.1~\text{m}\) apart (\(k=9\times10^{9}\)). Find \(F\).
A: \( F = k\frac{q^{2}}{r^{2}} = 9\times10^{9}\frac{(10^{-6})^{2}}{0.1^{2}} = 0.9~\text{N} \).

Section 5: Power & Efficiency

Q: Define power (mechanical).
A: Rate of doing work, \( P=\frac{W}{t} \) (W).
Q: Instantaneous power when a force \(F\) moves at speed \(v\).
A: \( P=Fv \).
Q: Define efficiency.
A: \( \eta=\frac{\text{useful output}}{\text{input}}\times100\% \).
Q: A motor lifts \(100~\text{kg}\) at \(0.5~\text{m s}^{-1}\). Required power (ignore losses)?
A: \( P=mgv=100\times9.8\times0.5=490~\text{W} \).
Q: A device has \(80~\text{J}\) input and \(56~\text{J}\) useful output. Efficiency?
A: \( \eta=\frac{56}{80}\times100\%=70\% \).

25 Problems & Solutions

Problem 1 (Thermal energy):
A \(0.5~\text{kg}\) kettle of water warms \(20^\circ\text{C}\to100^\circ\text{C}\) (\(c=4180~\text{J kg}^{-1}\text{K}^{-1}\)).
Solution: \(\Delta T=80~\text{K}\), \(Q=mc\Delta T=0.5\times4180\times80=1.672\times10^{5}~\text{J}\).
Problem 2 (Energy transfer):
A heater converts \(1000~\text{J}\) electrical into \(800~\text{J}\) heat.
Solution: Input: electrical; Useful output: thermal; Loss: \(200~\text{J}\) to surroundings.
Problem 3 (Pendulum):
A \(2~\text{kg}\) bob exchanges \(10~\text{J}\) between \(KE\) and \(GPE\) each half swing.
Solution: \(GPE \leftrightarrow KE\) (neglect losses).
Problem 4 (Efficiency fraction):
Car engine outputs \(2~\text{MJ}\) kinetic from \(5~\text{MJ}\) chemical.
Solution: \(\frac{2}{5}=0.4 \Rightarrow 40\%\).
Problem 5 (Closed system):
In a closed system, \(100~\text{J}\) of \(KE\) converts entirely to thermal.
Solution: Total energy remains \(100~\text{J}\); store changes from \(KE\) to thermal.
Problem 6 (Work & speed):
A \(50~\text{N}\) force pushes a \(10~\text{kg}\) box \(3~\text{m}\) from rest.
Solution: \(W=50\times3=150~\text{J}\Rightarrow \frac12(10)v^{2}=150\Rightarrow v=\sqrt{30}=5.48~\text{m s}^{-1}\).
Problem 7 (Braking work):
A \(1500~\text{kg}\) car brakes with \(4000~\text{N}\) over \(20~\text{m}\). Initial speed?
Solution: \(W=4000\times20=8.0\times10^{4}~\text{J}=\frac12(1500)v^{2}\Rightarrow v\approx 10.33~\text{m s}^{-1}\).
Problem 8 (Lifting crate):
Lift a \(15~\text{kg}\) crate \(2.5~\text{m}\) at constant speed.
Solution: \(W=mgh=15\times9.8\times2.5=367.5~\text{J}\).
Problem 9 (Resistive force):
Cyclist does \(5000~\text{J}\) of work against friction over \(2~\text{km}\).
Solution: \(F=\frac{W}{s}=\frac{5000}{2000}=2.5~\text{N}\).
Problem 10 (Bullet KE):
A \(0.02~\text{kg}\) bullet gains \(200~\text{J}\) of \(KE\).
Solution: \(\frac12(0.02)v^{2}=200\Rightarrow v=\sqrt{\frac{400}{0.02}}=\sqrt{20000}=141.4~\text{m s}^{-1}\).
Problem 11 (Spring PE):
Mass compresses spring (\(k=800~\text{N m}^{-1}\)) by \(0.10~\text{m}\).
Solution: \(E=\frac12 kx^{2}=\frac12(800)(0.1^{2})=4~\text{J}\).
Problem 12 (Gravitational \(\Delta E_p\) approx):
Satellite \(m=500~\text{kg}\) raised \(300~\text{km}\).
Solution (rough): \( \Delta E_p\approx mgh=500\times9.8\times3.0\times10^{5}=1.47\times10^{9}~\text{J}\) (constant-\(g\) approximation).
Problem 13 (Electric PE):
Move \(1~\text{C}\) through \(100~\text{V}\).
Solution: \(\Delta E = qV = 100~\text{J}\).
Problem 14 (Equipotential work):
Work done moving a charge along an equipotential?
Solution: \(0~\text{J}\).
Problem 15 (Pump power):
Water flow \(Q=2~\text{L s}^{-1}\) to height \(50~\text{m}\) (\(\rho=1000\)).
Solution: \(\dot m=\rho Q=2~\text{kg s}^{-1}\Rightarrow P=\dot m g h=2\times9.8\times50=980~\text{W}\).
Problem 16 (Gravitational field):
Two \(500~\text{kg}\) masses \(10~\text{m}\) apart. \(g\) at midpoint?
Solution: Fields equal and opposite → net \(g=0\).
Problem 17 (Parallel-plate \(E\)):
Plates \(2~\text{cm}\) apart, \(V=100~\text{V}\).
Solution: \( E=\frac{V}{d}=\frac{100}{0.02}=5.0\times10^{3}~\text{N C}^{-1}\).
Problem 18 (Electric force):
Charge \(2~\mu\text{C}\) in \(E=2000~\text{N C}^{-1}\).
Solution: \(F=qE=2\times10^{-6}\times2000=4.0\times10^{-3}~\text{N}\).
Problem 19 (Field lines):
Sketch field lines for a positive point charge.
Solution: Radially outward, denser near the charge.
Problem 20 (Vector \(g\)):
Net gravitational force on a \(2~\text{kg}\) at apex of isosceles triangle with two \(1~\text{kg}\) at base corners.
Solution: Vector sum of two equal attractions along the bisector; magnitude \(2F\cos(\frac{\theta}{2})\) where \(F\) is force from one base mass.
Problem 21 (Elevator power):
Elevator \(1000~\text{kg}\) ascends \(5~\text{m}\) in \(10~\text{s}\).
Solution: \( P=\frac{mgh}{t}=\frac{1000\times9.8\times5}{10}=4.9~\text{kW}\).
Problem 22 (Energy use):
Lamp \(60~\text{W}\) for \(4~\text{h}\).
Solution: \(E=Pt=60\times4~\text{Wh}=240~\text{Wh}=0.24~\text{kWh}=864~\text{kJ}\).
Problem 23 (Pump efficiency – revised):
Pump delivers \(Q=0.05~\text{m}^3\text{/s}\) to \(h=10~\text{m}\) using \(P_\text{in}=10~\text{kW}\). Find \(\eta\).
Solution: \(P_\text{useful}=\rho g Q h=1000\times9.8\times0.05\times10=4.9~\text{kW}\Rightarrow \eta=\frac{4.9}{10}\times100\%=49\%\). Numbers adjusted to keep \(\eta\le 100\%\).
Problem 24 (Lift speed):
A \(500~\text{W}\) motor lifts \(50~\text{kg}\). Max steady speed?
Solution: \( v=\frac{P}{mg}=\frac{500}{50\times9.8}=1.02~\text{m s}^{-1}\).
Problem 25 (Solar panel):
Panel \(\eta=15\%\), absorbs \(200~\text{W}\). Output?
Solution: \(0.15\times200=30~\text{W}\).

Have feedback or questions? We’d love to hear from you!

Course: Prep4Uni Physics 1