Topic 1: Quantities and Measurement
Course: Prep4Uni.Online Physics 1
Chapter 1: Quantities and Measurement
Chapter 2: Forces and Moments
Chapter 3: Motion and Forces
Chapter 4: Energy and Fields
Chapter 5: Projectile Motion
🚁Overview
This topic introduces the fundamental language of physics — the ability to describe, quantify, and measure physical phenomena. These foundational ideas underpin all topics in physics and engineering.
📖Contents
- Physical Quantities and SI Units
- Prefixes for Multiples and Submultiples
- Derived Units and Dimensional Homogeneity
- Errors and Uncertainties
- Scalars and Vectors
🎯 Learning Outcomes
By the end of this topic, you should be able to:
Recall and use SI base quantities and units
Convert units using SI prefixes
Use dimensional analysis to check equations
Identify types of measurement errors and estimate uncertainties
Distinguish between scalar and vector quantities
Add vectors using graphical and component methods
Table of Contents
1. Physical Quantities and SI Units
A physical quantity is anything that can be measured—length, time, mass, temperature, etc. Every quantity is expressed as a number and a unit. For example, \( 5.2~\mathrm{m} \) means a length whose numerical value is 5.2 and whose unit is the metre (\(\mathrm{m}\)).
SI Base Quantities and Units
The International System of Units (SI) defines seven base quantities. All other measurable quantities (called derived quantities) are built from these.
| Quantity | Unit name | Symbol |
|---|---|---|
| Length | metre | \(\mathrm{m}\) |
| Mass | kilogram | \(\mathrm{kg}\) |
| Time | second | \(\mathrm{s}\) |
| Electric current | ampere | \(\mathrm{A}\) |
| Thermodynamic temperature | kelvin | \(\mathrm{K}\) |
| Amount of substance | mole | \(\mathrm{mol}\) |
| Luminous intensity | candela | \(\mathrm{cd}\) |
Example
- Numerical value: \(2.10\)
- Unit: metre \((\mathrm{m})\)
Learning Check
Question: Which of the following is not an SI base quantity?
A. Speed B. Mass C. Time D. Temperature
Answer: A — Speed is a derived quantity because \( \text{speed} = \frac{\text{distance}}{\text{time}} \) with SI unit \( \mathrm{m\,s^{-1}} \).
Tip: Write numbers and units with a thin space and use unit exponents, e.g. \( 3.0~\mathrm{m\,s^{-2}} \) for acceleration and \( 25~^\circ\mathrm{C} \) for temperature.
2. Prefixes for Multiples and Submultiples
SI prefixes make it easier to express very large or very small numbers. Instead of writing out many zeros, these prefixes scale base units for clarity and simplicity.
| Prefix | Symbol | Factor |
|---|---|---|
| kilo | k | 10³ (1,000) |
| mega | M | 10⁶ |
| giga | G | 10⁹ |
| milli | m | 10⁻³ |
| micro | μ | 10⁻⁶ |
| nano | n | 10⁻⁹ |
Example 1: A 5 km road = 5 × 10³ m = 5000 m
Example 2: A computer processor operates at 3.2 GHz = 3.2 × 10⁹ Hz
✅ Learning Check: Convert the following:
- 1200 mm = ? m → Answer: 1.2 m
- 2.5 μs = ? s → Answer: 2.5 × 10⁻⁶ s
3. Derived Units and Dimensional Homogeneity
Derived units are combinations of SI base units used to express physical quantities that are not fundamental. They let us relate measurable quantities in a consistent, comparable way.
Examples of common derived units
- Speed: \( \displaystyle \text{speed}=\frac{\text{distance}}{\text{time}} \;\Rightarrow\; \mathrm{m\,s^{-1}} \)
- Acceleration: \( \displaystyle \text{acc}=\frac{\Delta \text{speed}}{\text{time}} \;\Rightarrow\; \mathrm{m\,s^{-2}} \)
- Force (Newton’s second law): \( \displaystyle F=ma \;\Rightarrow\; \mathrm{kg\,m\,s^{-2}} = \mathrm{N} \)
- Energy (work): \( \displaystyle E=F\,d \;\Rightarrow\; \mathrm{N\,m}=\mathrm{kg\,m^{2}\,s^{-2}} = \mathrm{J} \)
- Pressure: \( \displaystyle p=\frac{F}{A} \;\Rightarrow\; \frac{\mathrm{N}}{\mathrm{m^{2}}}=\mathrm{kg\,m^{-1}\,s^{-2}} = \mathrm{Pa} \)
Dimensional homogeneity means every term in a physical equation must have the same dimensions (e.g., all terms are lengths, or all are energies). Using the base dimensions \( [M] \) (mass), \( [L] \) (length), \( [T] \) (time), an equation is meaningful only if each term has identical \( [M^{a}L^{b}T^{c}] \).
Example (kinematics): Consider the equation of motion
\[ s = ut + \frac{1}{2} a t^{2}. \]
- \( u \) is initial velocity, units \( \mathrm{m\,s^{-1}} \) → dimensions \( [LT^{-1}] \).
- \( a \) is acceleration, units \( \mathrm{m\,s^{-2}} \) → dimensions \( [LT^{-2}] \).
- \( t \) is time, units \( \mathrm{s} \) → dimensions \( [T] \).
- \( s \) is displacement, units \( \mathrm{m} \) → dimensions \( [L] \).
Check each term: \( [ut]=[LT^{-1}]\![T]=[L] \), and \( [\frac12 a t^{2}]=[LT^{-2}]\![T^{2}]=[L] \). ✅ Both terms on the right are lengths, matching \( s \). The equation is dimensionally consistent.
📐 Learning Check: Is \( F=ma \) dimensionally consistent?
Force: \( [F]=\mathrm{kg\,m\,s^{-2}} = [M L T^{-2}] \). Right-hand side: \( [m][a]=[M]\,[L T^{-2}]=[M L T^{-2}] \). ✅ Yes — both sides have the same dimensions and SI unit \( \mathrm{N} \).
Style tip: Write numbers and units with a thin space and upright units, e.g., \( 3.0~\mathrm{m\,s^{-2}} \), \( 25~^{\circ}\mathrm{C} \).
Learn how to instantly spot invalid physics equations using the principle of dimensional homogeneity! In this short tutorial, you’ll learn:
- ✅ What dimensional homogeneity means and why it’s a must-have check
- 🔍 Step-by-step how to compare units on both sides of any equation
- ⚠️ Common pitfalls to watch out for when you’re solving problems
- 📚 Real-world examples that demonstrate why mismatched dimensions always signal an error
By the end of this video, you’ll be able to scan any physics or engineering formula and verify its validity in seconds—no calculator required!
4. Errors and Uncertainties
Every measurement carries uncertainty—from instrument limits to human reading. Quantifying and propagating that uncertainty lets you report results honestly and compare them reliably.4.1 Types of Errors
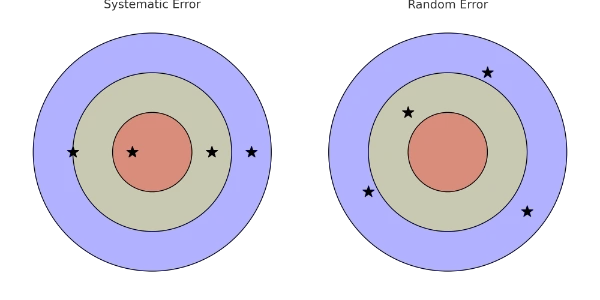
- Random errors: unpredictable scatter from reading to reading (e.g., display flicker, hand reaction time). They broaden the spread around the true value.
- Systematic errors: consistent bias that shifts all readings the same way (e.g., a scale with a non-zero offset). They move the average away from the true value.
4.2 Expressing Uncertainty
- Report as value ± absolute uncertainty, with matching decimal places, e.g. \( L = 25.4 \pm 0.2~\text{cm} \).
- Percent uncertainty: \( \%\Delta = \frac{\Delta x}{x}\times 100\% \).
4.3 Propagation of Uncertainty (quick rules)
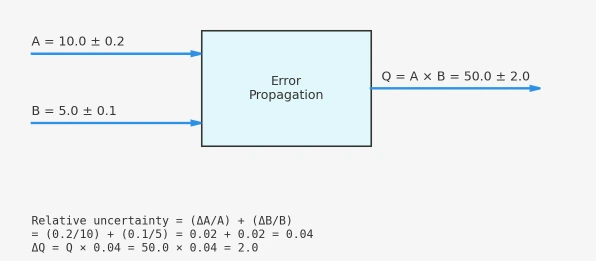
- Add/Subtract \( y = a \pm b \pm c \): add absolute uncertainties \( \Delta y = \Delta a + \Delta b + \Delta c \).
- Multiply/Divide \( y = \frac{a\,b}{c} \): add fractional (percentage) uncertainties \( \frac{\Delta y}{y} = \frac{\Delta a}{a} + \frac{\Delta b}{b} + \frac{\Delta c}{c} \).
- Powers \( y = a^{n} \): \( \frac{\Delta y}{y} = |n|\frac{\Delta a}{a} \).
4.4 Worked Example
- Measured time \( t = 2.00 \pm 0.05~\text{s} \), distance \( s = 10.0 \pm 0.2~\text{m} \).
- Speed \( v = \frac{s}{t} \).
Fractional uncertainties: \[ \frac{\Delta s}{s} = \frac{0.2}{10.0} = 0.020 \quad(2.0\%), \qquad \frac{\Delta t}{t} = \frac{0.05}{2.00} = 0.025 \quad(2.5\%). \] Combine (product/quotient rule): \[ \frac{\Delta v}{v} = \frac{\Delta s}{s} + \frac{\Delta t}{t} = 0.020 + 0.025 = 0.045. \] Best value: \[ v = \frac{10.0}{2.00} = 5.00~\text{m\,s}^{-1}. \] Absolute uncertainty: \[ \Delta v = 0.045 \times 5.00 \approx 0.225 \approx 0.23~\text{m\,s}^{-1}. \]
Report: \( v = 5.00 \pm 0.23~\mathrm{m\,s^{-1}} \) (value rounded to the same decimal place as the uncertainty).
✅ Learning Check: Add \(12.0 \pm 0.2~\mathrm{cm}\) and \(8.0 \pm 0.1~\mathrm{cm}\).
Answer: Absolute uncertainties add: \( \Delta L = 0.2 + 0.1 = 0.3~\mathrm{cm} \).
Total: \( L = 12.0 + 8.0 = 20.0~\mathrm{cm} \).
Report: \( 20.0 \pm 0.3~\mathrm{cm} \).
5. Scalars and Vectors
- Scalar: magnitude only (e.g., speed, time, energy, temperature).
- Vector: magnitude and direction (e.g., velocity, force, displacement, momentum).
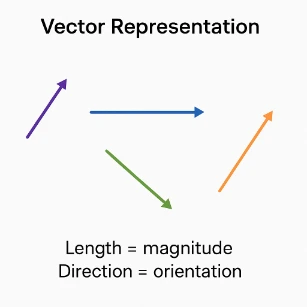
Vector Representation
- Draw an arrow: length = magnitude, orientation = direction.
- Notation (all equivalent): \( \vec{v} \), bold \( \mathbf{v} \), or italic \( v \) with an arrow in diagrams.
- In 2D Cartesian components: \( \vec{v} = (v_x,\,v_y) \) or \( \vec{v} = v_x\,\hat{\imath} + v_y\,\hat{\jmath} \).
- Magnitude (length): \( \|\vec{v}\| = \sqrt{v_x^{2} + v_y^{2}} \).
- Direction angle from the +x axis: \( \theta = \tan^{-1}\!\left(\frac{v_y}{v_x}\right) \) (use quadrant-aware arctan).
Vector Addition Methods
- Tip-to-tail method: place the tail of the second vector at the tip of the first; the resultant \( \vec{R} \) runs from the free tail to the free tip.
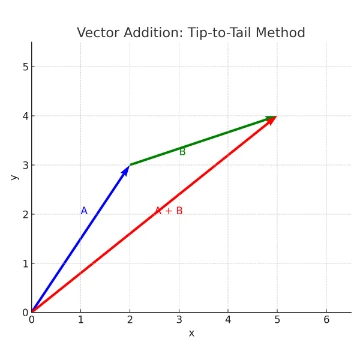
- Parallelogram method: draw both vectors from a common origin and complete the parallelogram; the diagonal is \( \vec{R} \).
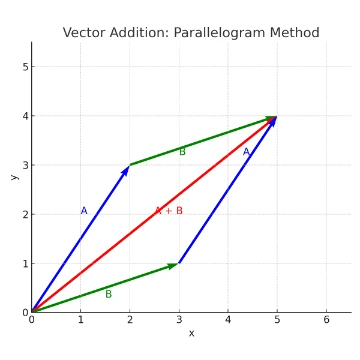
- Component method (most useful for calculation): resolve into \( x \) and \( y \) components and add them separately: \[ \vec{R} = \vec{A} + \vec{B} \quad\Rightarrow\quad \begin{cases} R_x = A_x + B_x,\\ R_y = A_y + B_y \end{cases} \qquad \|\vec{R}\| = \sqrt{R_x^{2} + R_y^{2}},\quad \theta_R = \arctan\!\left(\frac{R_y}{R_x}\right). \]
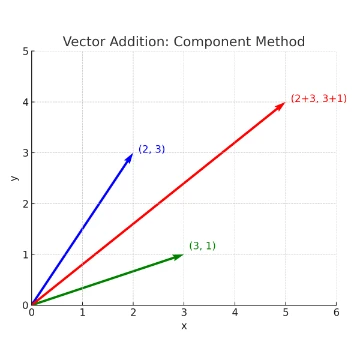
Worked Example: Resultant Displacement
A plane flies \(100~\text{km}\) east, then \(80~\text{km}\) north.
- Components: \( \vec{R} = (100,\,80)~\text{km} \).
- Magnitude: \[ \|\vec{R}\| = \sqrt{100^{2} + 80^{2}} = \sqrt{16400} \approx 128.1~\text{km}. \]
- Direction: \[ \theta = \tan^{-1}\!\left(\frac{80}{100}\right) \approx \mathbf{38.7^{\circ}}\ \text{north of east}. \]
✅ Learning Check: A force \( F = 50~\text{N} \) acts at \( 30^{\circ} \) above the horizontal. Find its components.
- Horizontal: \( F_x = F\cos 30^{\circ} = 50\cos 30^{\circ} \approx \mathbf{43.3}~\text{N}. \)
- Vertical: \( F_y = F\sin 30^{\circ} = 50\sin 30^{\circ} = \mathbf{25.0}~\text{N}. \)
Tip: for angles to the horizontal, use \( (\cos\theta,\,\sin\theta) \); to the vertical, swap to \( (\sin\theta,\,\cos\theta) \).
Vector Addition: Three Essential Methods — This short video demonstrates how to combine vectors using the Tip-to-Tail method, the Parallelogram method, and the Component method, helping learners visualise and calculate vector sums with clarity.
| Concept | Definition / Formula |
|---|---|
| Physical Quantity |
A measurable property expressed as value + unit
(e.g., 5.2 m, 3.0 s). |
| SI Base Units | Length (m), Mass (kg), Time (s), Electric current (A), Temperature (K), Amount of substance (mol), Luminous intensity (cd) |
| SI Prefixes | kilo (k, \(10^{3}\)), mega (M, \(10^{6}\)), giga (G, \(10^{9}\)), milli (m, \(10^{-3}\)), micro (µ, \(10^{-6}\)), nano (n, \(10^{-9}\)) |
| Derived Units & Dimensional Homogeneity | Combine base units, e.g., force: \( \mathrm{N} = \mathrm{kg\; m\; s^{-2}} \). Equations must be dimensionally consistent (each term with the same dimensions). |
| Measurement Uncertainty | Report as value \( \pm \) uncertainty (e.g., \( 25.4 \pm 0.2~\mathrm{cm} \)). For \(+\)/\( – \): add absolute uncertainties; for \( \times \)/\( \div \): add percentage uncertainties. |
| Random vs Systematic Errors | Random: unpredictable scatter about a mean. Systematic: consistent bias (e.g., zero offset). |
| Scalars & Vectors | Scalar: magnitude only (e.g., time, energy). Vector: magnitude and direction (e.g., displacement, velocity). Magnitude example: \( \|\vec{v}\| = \sqrt{v_x^{2} + v_y^{2}} \). |
| Vector Addition | Graphical: tip-to-tail or parallelogram. Component form (2D): \( \vec{R}=\vec{A}+\vec{B} \Rightarrow R_x=A_x+B_x,\; R_y=A_y+B_y,\; \|\vec{R}\|=\sqrt{R_x^{2}+R_y^{2}} \). |
Proceed to: Topic 2: Forces and Moments
Return to Prep4Uni Physics 1
Additional Resources:
📝EXERCISES
Questions and Answers (Try each question before revealing the answer)
Section 1: Physical Quantities and SI Units
- What are the seven SI base quantities?
Answer: Length, mass, time, electric current, thermodynamic temperature, amount of substance, luminous intensity.
(All other physical quantities are derived from these.) - State the SI base unit for electric current.
Answer: Ampere (A). 1 A corresponds to a specific electromagnetic definition based on the elementary charge. - Which SI unit is used to measure temperature?
Answer: Kelvin (K). Kelvin is absolute temperature measured from absolute zero. - Which physical quantity is measured in kilograms (kg)?
Answer: Mass. Mass quantifies the amount of matter/inertia. - What is the SI unit for time?
Answer: Second (s). Defined via the cesium-133 atomic transition.
Section 2: Prefixes for Multiples and Submultiples
- What is the prefix for \(10^{6}\)?
Answer: Mega (M): \(1~\text{Mm}=10^{6}\,\text{m}\). - Convert \(5~\text{mm}\) to metres.
Answer: \(5~\text{mm}=5\times10^{-3}~\text{m}=0.005~\text{m}\).
(Because \(1~\text{mm}=10^{-3}~\text{m}\).) - What does the prefix “nano” represent?
Answer: \(10^{-9}\). Example: \(1~\text{ns}=10^{-9}~\text{s}\). - Express \(0.000001~\text{s}\) using a prefix.
Answer: \(1~\mu\text{s}\) (microsecond), since \(1~\mu\text{s}=10^{-6}~\text{s}\). - How many metres are there in \(2.5~\text{km}\)?
Answer: \(2.5~\text{km}=2.5\times10^{3}~\text{m}=2500~\text{m}\).
Section 3: Derived Units and Dimensional Homogeneity
- What is the SI unit for force?
Answer: Newton (N), where \(1~\text{N}=1~\text{kg}\,\text{m}\,\text{s}^{-2}\). - Show that the unit of force (N) is a derived unit.
Answer: From \(F=ma\): \([F]=[\text{kg}]\,[\text{m}\,\text{s}^{-2}]=\text{kg}\,\text{m}\,\text{s}^{-2}=\text{N}\). - Write the dimensions of kinetic energy.
Answer: \(K=\frac{1}{2}mv^{2}\Rightarrow [K]=\mathrm{M}\,(\mathrm{L}\,\mathrm{T}^{-1})^{2}=\mathrm{M}\,\mathrm{L}^{2}\,\mathrm{T}^{-2}\). - Check if the equation \(s=ut+\frac{1}{2}at^{2}\) is dimensionally consistent.
Answer: \([s]=\mathrm{L}\), \([ut]=(\mathrm{L}\,\mathrm{T}^{-1})\,\mathrm{T}=\mathrm{L}\), \([at^{2}]=(\mathrm{L}\,\mathrm{T}^{-2})\,\mathrm{T}^{2}=\mathrm{L}\). All are length \(\Rightarrow\) consistent. - What is meant by dimensional homogeneity?
Answer: Every term in a physical equation has the same dimensions, ensuring physical and algebraic consistency.
Section 4: Errors and Uncertainties
- Name two types of systematic errors.
Answer: Zero error and calibration error. Both shift all readings in one direction. - What is the difference between random error and systematic error?
Answer: Random errors cause unpredictable scatter (reduced by averaging). Systematic errors are consistent biases (require correction/recalibration). - A length is measured as \(15.2\pm0.1~\text{cm}\). What is the percentage uncertainty?
Answer: \(\frac{0.1}{15.2}\times100\%\approx0.66\%\). - If two quantities \(A=5.0\pm0.2\) and \(B=3.0\pm0.1\) are added, what is the uncertainty in \(A+B\)?
Answer: Add absolute uncertainties: \(\pm(0.2+0.1)=\pm0.3\). - What is the best way to reduce random errors?
Answer: Take repeated measurements and average them; also improve resolution and consistent experimental technique.
Section 5: Scalars and Vectors
- Define scalar quantity and give an example.
Answer: A scalar has magnitude only (no direction). Example: temperature, mass, energy. - Define vector quantity and give an example.
Answer: A vector has magnitude and direction. Example: velocity, displacement, force. - Is mass a scalar or a vector?
Answer: Scalar. It has no directional property. - How can vectors be added graphically?
Answer: Tip-to-tail method or parallelogram method. Both yield the same resultant. - A displacement of \(4~\text{m}\) east is added to \(3~\text{m}\) north. What is the resultant magnitude?
Answer: Using Pythagoras:
\[
R=\sqrt{4^{2}+3^{2}}=\sqrt{25}=5~\text{m}.
\]
Direction: \(\theta=\tan^{-1}\!\left(\frac{3}{4}\right)\approx36.9^{\circ}\) north of east.
Problems and Solutions 1 (Try each before peeking!)
Problem 1: A car travels 240 km in 3 hours. What is its average speed in m/s?
Solution:
Convert to SI units:
\[
240~\text{km}=240{,}000~\text{m},\qquad 3~\text{h}=3\times 3600=10{,}800~\text{s}.
\]
Average speed
\[
\bar v=\frac{\text{distance}}{\text{time}}
=\frac{240{,}000}{10{,}800}\approx 22.2~\text{m}\,\text{s}^{-1}.
\]
Tip: \(240~\text{km}/3~\text{h}=80~\text{km}\,\text{h}^{-1}\), and \(80/3.6\approx 22.2~\text{m}\,\text{s}^{-1}\).
Problem 2: Convert \(5.6\times 10^{-3}\ \text{m}\) into a unit with a prefix.
Solution:
Since \(1~\text{mm}=10^{-3}~\text{m}\),
\[
5.6\times 10^{-3}~\text{m}=5.6~\text{mm}\ (\text{millimetres}).
\]
Problem 3: The unit of energy is the joule (J). Show it matches \(E=\frac{1}{2}mv^{2}\) dimensionally.
Solution:
From \(E=\frac{1}{2}mv^{2}\),
\[
[E]=[\mathrm{M}]\,[\mathrm{L}\,\mathrm{T}^{-1}]^{2}
=\mathrm{M}\,\mathrm{L}^{2}\,\mathrm{T}^{-2}.
\]
Since \(1~\mathrm{J}=1~\mathrm{kg}\,\mathrm{m}^{2}\,\mathrm{s}^{-2}\), it follows that
\([E]=\mathrm{M}\,\mathrm{L}^{2}\,\mathrm{T}^{-2}\).
Consistent.
Problem 4: A stopwatch reads \(3.52~\text{s}\), least count \(0.01~\text{s}\). Find absolute and percentage uncertainty.
Solution:
Absolute uncertainty: \(\pm 0.01~\text{s}\).
Percentage uncertainty:
\[
\frac{0.01}{3.52}\times 100\% \approx 0.284\% \approx 0.28\%.
\]
Note: Some labs take \(\pm\frac{\text{least count}}{2}\) if you can interpolate; here we use the full least count.
Problem 5: Two masses \(A=5.0\pm 0.2~\mathrm{kg}\) and \(B=3.0\pm 0.1~\mathrm{kg}\). Find the total mass and its uncertainty.
Solution:
For addition/subtraction, add absolute uncertainties:
\[
m_{\mathrm{tot}} = 5.0+3.0 = 8.0~\mathrm{kg},\qquad
\Delta m = 0.2+0.1 = 0.3~\mathrm{kg}.
\]
Therefore, the result is \(8.0\pm 0.3~\mathrm{kg}\).
Problem 6: Is \(s=v t^{2}\) dimensionally consistent?
Solution:
LHS: \([s]=\mathrm{L}\). RHS: \([v t^{2}]=(\mathrm{L}\,\mathrm{T}^{-1})\,\mathrm{T}^{2}=\mathrm{L}\,\mathrm{T}\).
Since \(\mathrm{L}\neq \mathrm{L}\,\mathrm{T}\), the equation is not dimensionally consistent.
Problem 7: Express \(1.2\times 10^{9}~\text{Hz}\) using a prefix.
Solution:
\[
1.2\times 10^{9}~\text{Hz}=1.2~\text{GHz}\ (\text{gigahertz}).
\]
Problem 8: Add a vector \(6~\text{m}\) at \(30^\circ\) to another \(4~\text{m}\) at \(120^\circ\). Find resultant magnitude (use components).
Solution:
Let \(x\) be east, \(y\) be north. Resolve components:
\[
\begin{aligned}
\vec A &: A_x=6\cos 30^\circ=6\cdot \tfrac{\sqrt3}{2}\approx 5.196,\quad
A_y=6\sin 30^\circ=6\cdot \tfrac12=3.000;\\
\vec B &: B_x=4\cos 120^\circ=4\cdot(-\tfrac12)=-2.000,\quad
B_y=4\sin 120^\circ=4\cdot \tfrac{\sqrt3}{2}\approx 3.464.
\end{aligned}
\]
Totals:
\[
R_x=A_x+B_x\approx 3.196,\qquad R_y=A_y+B_y\approx 6.464.
\]
Magnitude and direction:
\[
\lVert\vec R\rVert=\sqrt{R_x^2+R_y^2}\approx \sqrt{(3.196)^2+(6.464)^2}
\approx \sqrt{52.0}\approx 7.21~\text{m},
\]
\[
\theta=\tan^{-1}\!\left(\frac{R_y}{R_x}\right)\approx \tan^{-1}(2.02)\approx 63.9^\circ
\ \text{(north of east)}.
\]
Problem 9: A reading of \(1.55~\text{m}\) is taken with a ruler marked in mm. What is the uncertainty and its percentage?
Solution:
Resolution \(=1~\text{mm}=0.001~\text{m}\). A common convention is \(\pm \text{one smallest division}\) if you cannot interpolate:
\[
\Delta L=\pm 0.001~\text{m},\qquad
\%\text{uncertainty}=\frac{0.001}{1.55}\times 100\%\approx 0.0645\%\approx 0.065\%.
\]
Note: If your lab uses half-division, \(\Delta L=\pm 0.0005~\text{m}\), giving \(\approx 0.032\%\).
Problem 10: The unit of pressure is the pascal (Pa). Express it in SI base units and dimensions.
Solution:
Pressure \(p=\frac{F}{A}\). Since \(1~\text{N}=1~\text{kg}\,\text{m}\,\text{s}^{-2}\) and \(A\) is \(\text{m}^2\):
\[
1~\text{Pa}=1~\frac{\text{N}}{\text{m}^{2}}
=\frac{\text{kg}\,\text{m}\,\text{s}^{-2}}{\text{m}^{2}}
=\text{kg}\,\text{m}^{-1}\,\text{s}^{-2}.
\]
Dimensions: \([p]=\mathrm{M}\,\mathrm{L}^{-1}\,\mathrm{T}^{-2}\).
Problems and Solutions 2 (Try to answer before looking at the solution)
1. Vector Addition (tip-to-tail — travel)
Problem: A hiker walks 4 km east, then 3 km north. What is the total displacement?
Solution:
Right triangle with legs 4 and 3 (km). Magnitude:
\[
|\vec{R}|=\sqrt{4^{2}+3^{2}}=\sqrt{25}=5~\text{km}.
\]
Direction from east (counter-clockwise):
\[
\theta=\tan^{-1}\!\left(\frac{3}{4}\right)\approx 36.9^\circ~\text{north of east}.
\]
Answer: \(5~\text{km}\) at \(36.9^\circ\) north of east (i.e., to the northeast).
2. Vector Addition (components — flight)
Problem: A plane flies 200 km due north, then 150 km due east. Find the resultant displacement.
Solution:
Components: \(R_x=150\), \(R_y=200\) (km). Magnitude:
\[
|\vec{R}|=\sqrt{150^{2}+200^{2}}=\sqrt{62500}=250~\text{km}.
\]
Bearing (east of north):
\[
\theta=\tan^{-1}\!\left(\frac{150}{200}\right)\approx 36.9^\circ~\text{east of north}.
\]
Answer: \(250~\text{km}\) at \(36.9^\circ\) east of north.
3. Vector Subtraction (geographical)
Problem: A ship sails 80 km north and then 50 km south. What is the final displacement?
Solution:
Opposite directions subtract:
\[
\Delta s=80-50=30~\text{km}~\text{north}.
\]
Answer: \(30~\text{km}\) north.
4. Vector Subtraction (wind correction)
Problem: A drone is intended to fly 100 m east but is blown 60 m west by wind. What is the actual displacement?
Solution:
Take east positive:
\[
R_x=+100+(-60)=40~\text{m}.
\]
Answer: \(40~\text{m}\) east.
5. Vector Addition (components with angles)
Problem: A vector of 10 m acts at \(30^\circ\), and another of 8 m at \(120^\circ\). Find the resultant.
Solution:
Resolve each:
\[
\begin{aligned}
x_1&=10\cos 30^\circ=8.66, & y_1&=10\sin 30^\circ=5.00,\\
x_2&=8\cos 120^\circ=-4.00, & y_2&=8\sin 120^\circ=6.93.
\end{aligned}
\]
Sum:
\[
R_x=8.66-4.00=4.66,\qquad R_y=5.00+6.93=11.93.
\]
Magnitude & angle (from +x):
\[
|\vec{R}|=\sqrt{4.66^{2}+11.93^{2}}\approx 12.73~\text{m},\quad
\theta=\tan^{-1}\!\left(\frac{11.93}{4.66}\right)\approx 68.5^\circ.
\]
Answer: \(12.73~\text{m}\) at \(68.5^\circ\) above +x (first quadrant).
6. Navigation (resultant velocity)
Problem: A boat heads north at \(5~\text{m s}^{-1}\) while a current pushes east at \(3~\text{m s}^{-1}\). What is the resultant velocity?
Solution:
\[
|\vec{v}|=\sqrt{5^{2}+3^{2}}=\sqrt{34}\approx 5.83~\text{m s}^{-1}.
\]
Direction (east of north):
\[
\theta=\tan^{-1}\!\left(\frac{3}{5}\right)\approx 31.0^\circ~\text{east of north}.
\]
Answer: \(5.83~\text{m s}^{-1}\) at \(31.0^\circ\) east of north.
7. Vector Subtraction (position change)
Problem: An object moves from \(A(3,2)\) to \(B(7,6)\). What is the displacement vector and its magnitude?
Solution:
\[
\vec{d}=\langle 7-3,\;6-2\rangle=\langle 4,4\rangle.
\]
\[
|\vec{d}|=\sqrt{4^{2}+4^{2}}=\sqrt{32}=5.66~\text{units}.
\]
Answer: \(\langle 4,4\rangle\) with magnitude \(5.66\).
8. Walking Path (component addition)
Problem: Walk \(6~\text{km}\) northeast, then \(6~\text{km}\) southeast. Find total displacement.
Solution:
Use \(45^\circ\):
\[
\text{NE}=\langle 6\cos45^\circ,\,6\sin45^\circ\rangle=\langle 4.24,\,4.24\rangle,
\]
\[
\text{SE}=\langle 6\cos45^\circ,\,-6\sin45^\circ\rangle=\langle 4.24,\,-4.24\rangle.
\]
Sum:
\[
\vec{R}=\langle 8.48,\,0\rangle \ \Rightarrow\ |\vec{R}|=8.48~\text{km}~\text{due east}.
\]
Answer: \(8.48~\text{km}\) due east.
9. Vector Addition (airplane with crosswind)
Problem: Airspeed \(300~\text{km h}^{-1}\) north; crosswind \(100~\text{km h}^{-1}\) from west. Find ground speed and direction.
Solution:
\[
|\vec{v}_g|=\sqrt{300^{2}+100^{2}}=\sqrt{100000}=316.2~\text{km h}^{-1}.
\]
\[
\theta=\tan^{-1}\!\left(\frac{100}{300}\right)\approx 18.4^\circ~\text{east of north}.
\]
Answer: \(316.2~\text{km h}^{-1}\) at \(18.4^\circ\) east of north.
10. Round-trip Displacement (grid city)
Problem: A taxi goes 5 blocks east, 3 north, 5 west, 3 south. What is the final displacement?
Solution:
Net east–west: \(5-5=0\). Net north–south: \(3-3=0\). So \(\vec{R}=\vec{0}\).
Answer: \(0\) (returns to the start).
📝 MORE EXERCISES
25 Learning-Check Questions & Answers (try first, then peek)
(5 from each subsection of “Forces & Moments”)
1. Types of Forces
- Q: What contact force acts perpendicular to a surface?
A: Normal reaction (acts ⟂ to the surface, balancing compression). - Q: Which force always opposes relative motion between two surfaces?
A: Friction \(f\) (static or kinetic), acts tangentially opposite motion/impending motion. - Q: Name the force that pulls on a mass hanging from a string.
A: Tension \(T\) (same magnitude along an ideal massless rope). - Q: What non-contact force acts downward on masses near Earth’s surface?
A: Weight \(W=mg\). - Q: Identify a viscous-drag example.
A: Air drag on a car, or water drag on a swimmer; often \(F_\text{drag}\propto v\) (low Re) or \(\propto v^{2}\) (high Re).
2. Hooke’s Law and Elastic Forces
- Q: State Hooke’s law.
A: \(F=kx\) (restoring force proportional to extension \(x\) within elastic limit). - Q: A spring stretches \(0.10~\text{m}\) under \(5~\text{N}\). Find \(k\).
A: \(k=F/x=5/0.10=50~\text{N m}^{-1}\). - Q: True/false: Hooke’s law holds for any extension.
A: False—only for small deformations (linear elastic region, below proportional limit). - Q: If \(k=200~\text{N m}^{-1}\), force to compress \(0.02~\text{m}\)?
A: \(F=kx=200\times0.02=4~\text{N}\). - Q: A spring has \(k=150~\text{N m}^{-1}\). Extension under \(3~\text{N}\)?
A: \(x=F/k=3/150=0.020~\text{m}\).
3. Moment and Torque
- Q: Define the moment of a force about a pivot.
A: \(M=F d_\perp\) where \(d_\perp\) is ⟂ distance from pivot to line of action. - Q: SI unit of moment?
A: Newton-metre (N·m). - Q: \(12~\text{N}\) applied at \(0.25~\text{m}\) from a hinge → moment?
A: \(M=12\times0.25=3~\text{N·m}\). - Q: Need \(10~\text{N·m}\) torque; you can apply \(20~\text{N}\). Lever arm?
A: \(d=M/F=10/20=0.50~\text{m}\). - Q: True/false: torque and moment are the same concept.
A: True (torque is a moment causing rotation; vector \( \boldsymbol{\tau}=\mathbf{r}\times\mathbf{F} \)).
4. Couples & Principle of Moments
- Q: What is a pure couple?
A: Two equal, opposite, parallel forces with separated lines of action → net force 0, net moment \(M=F s\) (with arm \(s\)). - Q: Couple from two \(15~\text{N}\) forces \(0.40~\text{m}\) apart?
A: \(M=15\times0.40=6.0~\text{N·m}\). - Q: State the principle of moments for rotational equilibrium.
A: \(\sum M_\text{clockwise}=\sum M_\text{anticlockwise}\) about any point. - Q: A \(20~\text{N}\) weight at \(1.5~\text{m}\) must be balanced at \(1.0~\text{m}\). Force?
A: \(20\times1.5=F\times1.0\Rightarrow F=30~\text{N}\). - Q: True/false: a couple produces translation.
A: False—pure rotation only.
5. Equilibrium Conditions
- Q: Two equilibrium conditions for a rigid body?
A: \(\sum \mathbf{F}=\mathbf{0}\) and \(\sum \mathbf{M}=\mathbf{0}\). - Q: A box at rest on a table: what is \(\sum F_y\)?
A: Zero (normal \(N\) equals weight \(mg\)). - Q: Name the diagram listing all forces on an object.
A: Free-body diagram (FBD). - Q: True/false: in static equilibrium, objects may rotate with constant angular speed.
A: False—static means no translation and no rotation. - Q: A beam in 2D equilibrium under three forces; how many equations?
A: Three: \(\sum F_x=0\), \(\sum F_y=0\), \(\sum M=0\).
20 Problems & Detailed Solutions (covering all five sections)
- Identify forces on a hanging mass
Problem: A \(5~\text{kg}\) mass hangs from a rope. List/draw forces.
Solution: Weight \(W=mg=5\times9.8=49~\text{N}\) downward; tension \(T=49~\text{N}\) upward for rest. (Net force \(=0\)). - Friction on a sliding block
Problem: \(m=2~\text{kg}\) on horizontal surface with \(\mu_k=0.30\). Friction?
Solution: Normal \(N=mg=19.6~\text{N}\). Kinetic friction \(f_k=\mu_k N=0.30\times19.6=5.88~\text{N}\) opposite motion. - Spring extension
Problem: \(k=100~\text{N m}^{-1}\) supports \(4~\text{kg}\). Extension?
Solution: At rest, \(kx=mg\Rightarrow x=mg/k=39.2/100=0.392~\text{m}\). - Stokes’ drag
Problem: Small sphere: \(v=0.10~\text{m s}^{-1}\), \(r=0.010~\text{m}\), \(\eta=0.50~\text{Pa·s}\). Drag?
Solution: \(F_d=6\pi\eta r v=6\pi(0.5)(0.01)(0.10)\approx9.42\times10^{-3}~\text{N}\). - Moment of a force
Problem: \(15~\text{N}\) ⟂ at \(0.20~\text{m}\). Moment?
Solution: \(M=F d=15\times0.20=3.0~\text{N·m}\). - Torque vector (2D)
Problem: \(\mathbf{F}=(0,20)\,\text{N}\) at \(\mathbf{r}=(0.5,0)\,\text{m}\). Torque about origin?
Solution: \(\tau_z=xF_y-yF_x=0.5\times20-0=10~\text{N·m}\) (into page by RH rule). - Balancing a couple
Problem: Two opposite \(10~\text{N}\) forces, arm \(0.50~\text{m}\). Moment?
Solution: \(M=F s=10\times0.50=5.0~\text{N·m}\). - Lever balance
Problem: \(50~\text{N}\) at \(2~\text{m}\) left; force at \(1~\text{m}\) right. Find \(F\).
Solution: \(\sum M=0:\ 50\times2=F\times1\Rightarrow F=100~\text{N}\). - Support reactions (uniform beam)
Problem: Uniform \(4~\text{m}\) beam, weight \(200~\text{N}\), supports at ends. Reactions?
Solution: Symmetry → \(R_A=R_B=100~\text{N}\) (weight acts at mid-span). - Atwood-like pulley
Problem: Masses \(3~\text{kg}\) and \(5~\text{kg}\) over frictionless pulley. \(a\) and \(T\)?
Solution: \(a=\frac{(5-3)g}{5+3}=2.45~\text{m s}^{-2}\). For light side: \(T=m(g+a)=3(9.8+2.45)=36.75~\text{N}\). - Spring–weight equilibrium
Problem: \(m=1~\text{kg}\), \(k=200~\text{N m}^{-1}\). Extension?
Solution: \(x=mg/k=9.8/200=0.049~\text{m}\). - Max static incline angle
Problem: \(\mu_s=0.40\). Largest \(\theta\) before sliding?
Solution: Threshold \(mg\sin\theta=\mu_s mg\cos\theta\Rightarrow \tan\theta=\mu_s\Rightarrow \theta\approx21.8^\circ\). - Will it slide?
Problem: \(m=2~\text{kg}\) on \(30^\circ\), \(\mu=0.20\).
Solution: Downslope \(=mg\sin30=9.8~\text{N}\). Normal \(=mg\cos30=16.97~\text{N}\). Max friction \(=0.2\times16.97=3.39~\text{N}\). Since \(9.8>3.39\) → it slides. - Centre of mass on a line
Problem: Masses: \(2~\text{kg}@0\), \(3~\text{kg}@2\), \(5~\text{kg}@5\) m. \(x_\text{CM}\)?
Solution: \(x_\text{CM}=\frac{2\cdot0+3\cdot2+5\cdot5}{2+3+5}=\frac{31}{10}=3.10~\text{m}\). - Simply supported beam with point load
Problem: Span \(6~\text{m}\); \(300~\text{N}\) at \(2~\text{m}\) from A. Reactions?
Solution: Moments about A: \(R_B\cdot6=300\cdot2\Rightarrow R_B=100~\text{N}\). Then \(R_A=300-100=200~\text{N}\). - Torque with an angle
Problem: \(F=50~\text{N}\) at \(30^\circ\) to a \(0.40~\text{m}\) arm. \(\tau\)?
Solution: \(\tau=rF\sin\theta=0.40\times50\times\sin30^\circ=10~\text{N·m}\). - Couple vs single force
Problem: Two \(20~\text{N}\) forces at \(\pm1~\text{m}\) (opposite directions). Show it’s a couple. Moment?
Solution: Net force \(=0\); net moment \(M=20\times(1-(-1))=40~\text{N·m}\). - Buoyant force
Problem: Cube side \(0.10~\text{m}\) fully submerged in water \(\rho=1000~\text{kg m}^{-3}\). \(F_b\)?
Solution: \(V=0.10^{3}=10^{-3}~\text{m}^{3}\). \(F_b=\rho g V=1000\cdot9.8\cdot10^{-3}=9.8~\text{N}\). - Magnetic force on a wire
Problem: \(I=0.50~\text{A}\), \(L=0.20~\text{m}\), \(B=0.30~\text{T}\) (⟂). Force?
Solution: \(F=ILB=0.50\times0.20\times0.30=0.030~\text{N}\). - Concurrent forces → equilibrium
Problem: Forces \(30~\text{N}\) at \(0^\circ\) and \(40~\text{N}\) at \(90^\circ\). Third force for equilibrium?
Solution: Resultant \(\vec{R}=\langle30,40\rangle\). Required \(\vec{F}_3=-\vec{R}=\langle-30,-40\rangle\). Magnitude \(=\sqrt{30^{2}+40^{2}}=50~\text{N}\). Direction \(=\tan^{-1}(40/30)\) below \(-x\) (i.e., \(216.9^\circ\) from +x).
Have feedback or questions? We’d love to hear from you!
Course: Prep4Uni Physics 1
Chapter 1: Quantities and Measurement
Chapter 2: Forces and Moments
Chapter 3: Motion and Forces
Chapter 4: Energy and Fields
Chapter 5: Projectile Motion
