Prepare for University Studies & Career Advancement

Pressure

Chapter 1: Pressure

Course: Prep4Uni Fluid Mechanics 1

Chapter 1: Pressure
Chapter 2: Variation of Pressure with Depth
Chapter 3: Pressure Measurement
Chapter 4: Buoyant Forces & Archimedes’ Principle
Chapter 5: Fluid Dynamics
Chapter 6: Bernoulli’s Equation
Chapter 7: Applications of Fluid Dynamics

🚁Overview

Pressure is the force applied perpendicular to a surface per unit area. In fluids, pressure at a point is exerted equally in all directions (isotropic).

📖Contents

  1. Definition
  2. SI Unit
  3. Gauge Vs Absolute Pressure
  4. Characteristics of Pressure in Fluids
  5. Example Calculation
  6. Key Formula Recap

🎯Learning Outcomes

  • Define pressure and express it mathematically as p = F/A, where F is the normal force and A is the area.
  • State the SI unit of pressure (pascal, Pa) and convert between Pa, kPa, bar, and atm.
  • Distinguish gauge vs. absolute pressure, and use pabs = pgauge + patm to relate them.
  • Describe the characteristics of pressure in fluids:
    • Acts perpendicular to any surface
    • Is uniform in all directions at a given depth
    • Increases with depth according to p = p₀ + ρ g h
  • Perform example calculations to compute pressure given force and area, and to convert between gauge and absolute pressures.
  • Recall and apply key formulas for pressure in problem-solving contexts.

Table of Contents

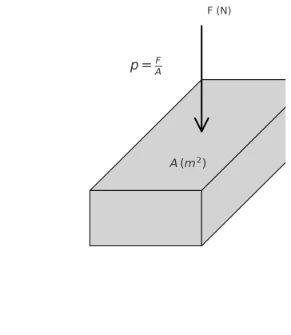
1.1 Definition

Pressure (p) is defined as:

p = F / A

where:

  • F = normal force (N)
  • A = area over which the force acts (m²)
Pressure = F / A
Pressure = F / A

1.2 SI Unit

The SI unit of pressure is the Pascal (Pa):

1 Pa = 1 N/m²

Common derived units:

  • kilopascal: 1 kPa = 10³ Pa
  • bar: 1 bar = 10⁵ Pa
  • atmosphere: 1 atm ≈ 1.013 × 10⁵ Pa

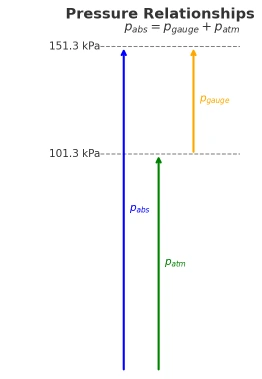
1.3 Gauge vs. Absolute Pressure

  • Absolute pressure (p_abs): measured relative to a perfect vacuum.
  • Gauge pressure (p_gauge): measured relative to ambient atmospheric pressure.

The relation between them is:

p_abs = p_gauge + p_atm

where p_atm ≈ 1.013 × 10⁵ Pa at sea level.

The diagram below shows the absolute pressure when the gauge pressure is 50 kPa

Gauge Pressure Verses Absolute Pressure
Gauge Pressure Verses Absolute Pressure

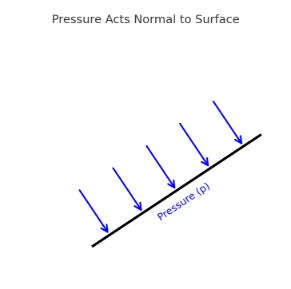
1.4 Characteristics of Pressure in Fluids

  • Pressure acts normal (perpendicular) to any surface.
Pressure acting normally on a surface
Pressure acting normally on a surface
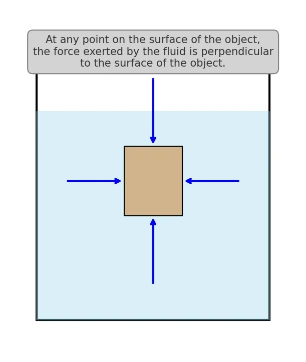
Pressure by liquid acting normally on the surface
Pressure by liquid acting normally on the surface
  • At a given depth in a static fluid, pressure is uniform in all directions.
Uniform Pressure at Same Depth
Uniform Pressure at Same Depth
Pressure Increases with Depth
Pressure Increases with Depth

1.5 Example Calculations

  1. Example 1: A force of 200 N is applied uniformly to a piston of area 0.02 m². What is the pressure?

    Solution:
    p = F / A = 200 N / 0.02 m² = 10 000 Pa = 10 kPa

  2. Example 2: A tire gauge reads 220 kPa (gauge). What is the absolute pressure inside the tire? (Take p_atm = 101 kPa)

    Solution:
    p_abs = p_gauge + p_atm = 220 kPa + 101 kPa = 321 kPa

1.6 Key Formula Recap

FormulaMeaning
p = F / APressure = force per unit area
1 Pa = 1 N/m²SI unit of pressure
p_abs = p_gauge + p_atmRelation between absolute and gauge pressure

Proceed to: Chapter 2: Variation of Pressure with Depth

Return to: Prep4Uni Fluid Mechanics 1

📝EXERCISES

20 Questions & Answers

1. What is pressure?

Pressure is the force applied perpendicular to a surface per unit area, given by p = F/A.

2. What is the SI unit of pressure?

The SI unit of pressure is the pascal (Pa), where 1 Pa = 1 N/m².

3. How many pascals are in 1 bar?

1 bar = 105 Pa.

4. Define gauge pressure.

Gauge pressure is measured relative to the ambient atmospheric pressure.

5. Define absolute pressure.

Absolute pressure is measured relative to a perfect vacuum.

6. State the relation between absolute and gauge pressure.

They are related by pabs = pgauge + patm, where patm ≈ 1.013 × 105 Pa.

7. What typical value does atmospheric pressure have at sea level?

About 1.013 × 105 Pa (≈ 101.3 kPa).

8. True or False: Pressure is a vector quantity.

False. Pressure is a scalar quantity.

9. True or False: In a fluid at rest, pressure acts equally in all directions at the same depth.

True.

10. How does pressure change if the same force is applied over a smaller area?

Pressure increases, since p = F/A and A decreases.

11. How does pressure change if the force doubles but area stays the same?

Pressure doubles, since p = F/A and F doubles.

12. Which instrument measures absolute pressure?

A sealed absolute pressure sensor or aneroid barometer.

13. Which device measures gauge pressure?

A tire-pressure gauge or Bourdon gauge.

14. What is vacuum pressure?

Vacuum pressure is gauge pressure below atmospheric, often expressed as a negative gauge reading.

15. Convert 50 kPa to Pa.

50 kPa = 50 000 Pa.

16. Convert 750 mmHg to pascals. (ρHg=13 600 kg/m³, g=9.81 m/s²)

p = ρgh = 13 600×9.81×0.75 ≈ 100 116 Pa.

17. Why is pressure in a fluid at rest isotropic?

Because fluid molecules transmit force equally in all directions at a point when at equilibrium.

18. What happens to pressure with increasing depth in a liquid?

Pressure increases linearly with depth according to p = p₀ + ρgh.

19. Explain why pressure units must balance dimensionally in equations.

Dimensional homogeneity requires both sides of an equation to have the same units, ensuring physical validity.

20. What is the pressure under 10 m of freshwater? (ρ=1000 kg/m³, g=9.81 m/s²)

p = 1000×9.81×10 ≈ 9.81×104 Pa (≈ 98.1 kPa) above surface pressure.

 

10 Problems & Solutions

  1. Problem 1: A piston of area 0.02 m² supports a load of 500 N. What pressure does it exert?

    Solution:
    p = F/A = 500 N / 0.02 m² = 25 000 Pa.

  2. Problem 2: To produce 10 kPa of pressure, what area must a 200 N force act on?

    Solution:
    A = F/p = 200 N / 10 000 Pa = 0.02 m².

  3. Problem 3: A tire gauge reads 220 kPa (gauge). What is the absolute pressure inside the tire? (p_atm=101 kPa)

    Solution:
    p_abs = p_gauge + p_atm = 220 kPa + 101 kPa = 321 kPa.

  4. Problem 4: A boiler shows 2 bar gauge. Find its absolute pressure in pascals.

    Solution:
    2 bar = 2×105 Pa; p_abs = 200 000 + 101 300 ≈ 301 300 Pa.

  5. Problem 5: Convert 1 atm to pascals and to mmHg.

    Solution:
    1 atm = 1.013×105 Pa ≈ 760 mmHg.

  6. Problem 6: A hydraulic ram has piston area 0.1 m² and gauge pressure 3 MPa. What force does it exert?

    Solution:
    F = p×A = 3×106 Pa × 0.1 m² = 3×105 N.

  7. Problem 7: Atmospheric pressure acts on a 2 m² roof. Calculate the total force. (p_atm=1.013×105 Pa)

    Solution:
    F = p×A = 1.013×105 Pa × 2 m² ≈ 2.026×105 N.

  8. Problem 8: Find the gauge pressure at 10 m depth in water. (ρ=1000 kg/m³, g=9.81 m/s²)

    Solution:
    p = ρ g h = 1000×9.81×10 ≈ 9.81×104 Pa (≈ 98.1 kPa).

  9. Problem 9: In a U-tube manometer, mercury (ρ=13 600 kg/m³) shows a 0.1 m difference. Find gauge pressure.

    Solution:
    p_gauge = ρ g h = 13 600×9.81×0.1 ≈ 13 340 Pa.

  10. Problem 10: A vacuum pump reads −80 kPa (gauge). What is the absolute pressure?

    Solution:
    p_abs = p_gauge + p_atm = −80 kPa + 101 kPa = 21 kPa.