Buoyant Forces and Archimedes' Principle - Student Guide

Chapter 4: Buoyant Forces & Archimedes’ Principle

Chapter 1: Pressure
Chapter 2: Variation of Pressure with Depth
Chapter 3: Pressure Measurement
Chapter 4: Buoyant Forces & Archimedes’ Principle
Chapter 5: Fluid Dynamics
Chapter 6: Bernoulli’s Equation
Chapter 7: Applications of Fluid Dynamics

🚁Overview

Any object submerged in (or floating on) a fluid experiences an upward buoyant force equal to the weight of the fluid it displaces. In this chapter you will:

State and apply Archimedes’ principle.
Calculate buoyant forces on fully and partially submerged bodies.
Determine the conditions for flotation and assess stability of floating objects.

📖Contents

Archimedes’ Principle
Buoyant Force Calculations
Flotation & Stability

🎯Learning Outcomes

In this chapter you will:

State and apply Archimedes’ principle.
Calculate buoyant forces on fully and partially submerged bodies.
Determine the conditions for flotation and assess stability of floating objects.

4.1 Archimedes’ Principle

Archimedes’ principle:
A body immersed in a fluid is buoyed up by a force equal to the weight of the fluid displaced: \( F_b = \rho_{\mathrm{fluid}} \, g \, V_{\mathrm{disp}} \).

Archimedes’ Principle: Verifying a Crown’s Purity

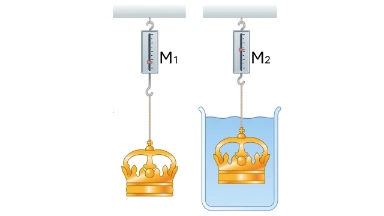
When an object is weighed in air and then again while fully submerged in water, the apparent loss of weight \( M_{\mathrm{air}} – M_{\mathrm{water}} \) is the buoyant force. Since the crown is fully submerged, the displaced-water volume equals the crown’s volume.

Given: \( M_{\mathrm{air}}=7.84~\mathrm{N} \), \( M_{\mathrm{water}}=6.84~\mathrm{N} \).

Buoyant force: \( F_b = M_{\mathrm{air}}-M_{\mathrm{water}}=1.00~\mathrm{N} \).

Mass of the crown: \( m_{\mathrm{crown}}=\frac{M_{\mathrm{air}}}{g} =\frac{7.84}{9.81}\,\mathrm{kg}\approx 0.800~\mathrm{kg} \).

Mass of displaced water: \( m_{\mathrm{water}}=\frac{F_b}{g} =\frac{1.00}{9.81}\,\mathrm{kg}\approx 0.102~\mathrm{kg} \).

Volume of displaced water (crown’s volume): \( V=\frac{m_{\mathrm{water}}}{\rho_{\mathrm{water}}} =\frac{0.102}{1000}\,\mathrm{m}^3 \approx 1.02\times 10^{-4}\,\mathrm{m}^3 \).

Density of the crown: \( \rho_{\mathrm{crown}}=\frac{m_{\mathrm{crown}}}{V} \approx \frac{0.800}{1.02\times 10^{-4}} \,\mathrm{kg\,m^{-3}} \approx 7.84\times 10^{3}\,\mathrm{kg\,m^{-3}}. \)

Gold has \( \approx 1.932\times 10^{4}\,\mathrm{kg\,m^{-3}} \), so the crown is not pure gold.

4.2 Buoyant Force Calculations

Fully submerged: \( F_b=\rho_f g V_{\mathrm{obj}} \).
Floating (partially submerged): \( \rho_f g V_{\mathrm{disp}} = m_{\mathrm{obj}} g \Rightarrow F_b=W_{\mathrm{obj}} \).
Net force: \( F_{\mathrm{net}} = F_b – W = \rho_f g V_{\mathrm{disp}} – \rho_{\mathrm{obj}} g V_{\mathrm{obj}} \).

4.3 Flotation & Equilibrium

Condition for flotation: \( \rho_f V_{\mathrm{disp}}=\rho_{\mathrm{obj}} V_{\mathrm{obj}} \).
Equilibrium (no net moment): the line of action of \( F_b \) through the center of buoyancy \( B \) should pass through the center of gravity \( G \).

4.4 Stability of Floating Bodies

For a small heel, the buoyant-force line meets the vertical through \( G \) at the metacenter \( M \). The metacentric height is \( GM \):

\( BM=\frac{I}{V_{\mathrm{disp}}} \) (waterplane second moment \( I \) about the heel axis).
\( GM=BM-BG \).
Stable: \( GM>0 \) → righting moment. Unstable: \( GM<0 \) → overturning moment.

Example: For a rectangular barge with beam \( b \), length \( L \): \( I=\frac{b^{3}L}{12} \). Use this to compute \( BM \) and compare with \( BG \).

4.5 Partially Submerged Objects

How Much of an Iceberg Is Hidden?

\( \rho_{\mathrm{ice}}=917\,\mathrm{kg\,m^{-3}} \)
\( \rho_{\mathrm{water}}=1025\,\mathrm{kg\,m^{-3}} \)

Floating equilibrium gives \( \rho_{\mathrm{water}} V_{\mathrm{disp}} = \rho_{\mathrm{ice}} V_{\mathrm{ice}} \). Hence the fraction submerged is \[ \frac{V_{\mathrm{disp}}}{V_{\mathrm{ice}}} = \frac{\rho_{\mathrm{ice}}}{\rho_{\mathrm{water}}} = \frac{917}{1025} \approx 0.8946 \ (89.46\%). \] So about \(10.5\%\) is above the surface.

4.6 Worked Examples

Example 1: Metal cube \(a=0.1~\mathrm{m}\), \( \rho_{\mathrm{obj}}=7800 \), water \( \rho_f=1000 \).
\( V=a^{3}=1.0\times 10^{-3}\ \mathrm{m^{3}} \).
\( F_b=\rho_f g V\approx 9.81~\mathrm{N} \).
\( W=\rho_{\mathrm{obj}} g V\approx 76.5~\mathrm{N} \).
\( F_{\mathrm{net}}=F_b-W\approx -66.7~\mathrm{N} \) (downward).
Example 2: Wooden block \( \rho_{\mathrm{obj}}=600 \), \( V=0.02~\mathrm{m^{3}} \) in water.
Flotation: \( \frac{V_{\mathrm{disp}}}{V_{\mathrm{obj}}}=\frac{\rho_{\mathrm{obj}}}{\rho_f}=0.6 \Rightarrow 60\% \) submerged.

4.7 Example Problems & Solutions

Problem 1: Sphere \( r=0.2~\mathrm{m} \) in oil \( \rho=850 \). Find \( F_b \).
Solution: \( V=\frac{4}{3}\pi r^{3}=\frac{4}{3}\pi(0.2)^{3}\approx 3.351\times 10^{-2}\ \mathrm{m^{3}} \).
\( F_b=\rho g V\approx 2.79\times 10^{2}\ \mathrm{N}. \)
Problem 2: Log \( r=0.05~\mathrm{m}, L=1~\mathrm{m}, \rho=700 \) in freshwater.
Solution: \( V_{\mathrm{obj}}=\pi r^{2}L\approx 7.85\times 10^{-3}\ \mathrm{m^{3}} \).
Fraction submerged \( = \rho_{\mathrm{obj}}/\rho_f = 0.7 \).
\( V_{\mathrm{disp}}=0.7 V_{\mathrm{obj}}\approx 5.50\times 10^{-3}\ \mathrm{m^{3}} \).
\( h=\frac{V_{\mathrm{disp}}}{\pi r^{2}}\approx 0.70~\mathrm{m}. \)
Problem 3: Explain effect of metacentric height \( GM \) on stability.
Solution: \( GM>0 \Rightarrow \) righting moment (stable). \( GM<0 \Rightarrow \) overturning moment (unstable).
Problem 4: Barge with waterplane inertia \( I=3\,\mathrm{m^{4}} \), displaced volume \( V=20\,\mathrm{m^{3}} \), and \( BG=0.3\,\mathrm{m} \). Find \( GM \).
Solution: \( BM=\frac{I}{V}=0.15\,\mathrm{m} \), hence \( GM=BM-BG=0.15-0.30=-0.15\,\mathrm{m}<0 \) → unstable.

4.8 Key Formula Recap

Formula	Description
\( F_b = \rho_f \, g \, V_{\mathrm{disp}} \)	Buoyant force = weight of displaced fluid
\( \frac{V_{\mathrm{disp}}}{V_{\mathrm{obj}}} = \frac{\rho_{\mathrm{obj}}}{\rho_f} \)	Fraction submerged for floating bodies
\( F_{\mathrm{net}} = F_b – \rho_{\mathrm{obj}}\, g \, V_{\mathrm{obj}} \)	Net force on a (fully) submerged object
\( GM = BM – BG \)	Metacentric height for stability analysis

Proceed to: Chapter 5: Fluid Dynamics

Return to: Prep4Uni Fluid Mechanics 1

📝EXERCISES

20 Questions & Answers

1. What is the buoyant force?
The buoyant force is the net upward force a fluid exerts on an immersed body. Its magnitude equals the weight of the displaced fluid: \( F_b=\rho_{\text{fluid}}\,g\,V_{\text{disp}} \).
2. State Archimedes’ principle.
A body wholly or partially immersed in a fluid experiences an upward force equal to the weight of the fluid it displaces: \( F_b=\rho_{\text{fluid}}\,g\,V_{\text{disp}} \).
3. Write the formula for buoyant force.
\( F_b=\rho_{\text{fluid}}\,g\,V_{\text{disp}} \), where \( \rho_{\text{fluid}} \) is fluid density, \( g \) gravitational acceleration, and \( V_{\text{disp}} \) displaced volume.
4. What is the unit of buoyant force?
Newton, \( \mathrm{N}=\mathrm{kg\,m\,s^{-2}} \).
5. How do you compute the displaced volume of a floating object?
Force balance at equilibrium: \( F_b=W \Rightarrow \rho_f g V_{\text{disp}} = m_{\text{obj}} g \). Hence \( V_{\text{disp}}=\frac{m_{\text{obj}}}{\rho_f}=\frac{\rho_{\text{obj}}V_{\text{obj}}}{\rho_f} \).
6. What fraction of a floating body is submerged?
\( \frac{V_{\text{disp}}}{V_{\text{obj}}}=\frac{\rho_{\text{obj}}}{\rho_{\text{fluid}}} \).
7. Under what condition does an object sink?
If \( \rho_{\text{obj}}>\rho_f \) so that \( \rho_f g V_{\text{obj}} < \rho_{\text{obj}} g V_{\text{obj}} \), it sinks.
8. Define center of buoyancy.
The point \( B \) at the centroid of the displaced-fluid volume; the buoyant force acts through \( B \).
9. What is metacentric height?
\( GM \) is the distance between center of gravity \( G \) and metacenter \( M \) for small heel angles.
10. What is the condition for stable flotation?
\( GM>0 \Rightarrow \) righting moment (stable). \( GM<0 \Rightarrow \) overturning moment (unstable).
11. How does density affect flotation?
\( \frac{V_{\text{disp}}}{V_{\text{obj}}}=\frac{\rho_{\text{obj}}}{\rho_f} \): denser objects submerge more.
12. Why can an object have no net force if weightless?
Without gravity there is no hydrostatic gradient; integrated pressure forces cancel so net \( F_b=0 \).
13. How do you find the submerged depth of a floating cylinder?
\( V_{\text{disp}}=\pi r^{2} h_{\text{sub}} \) and \( \rho_f g (\pi r^{2} h_{\text{sub}})=\rho_{\text{obj}} g (\pi r^{2} H) \Rightarrow h_{\text{sub}}=H\,\frac{\rho_{\text{obj}}}{\rho_f} \).
14. What happens to buoyant force if fluid density doubles?
\( F_b\propto \rho_f \); doubling \( \rho_f \) doubles \( F_b \) for the same \( V_{\text{disp}} \).
15. Can Archimedes’ principle be applied to gases?
Yes: \( F_b=\rho_{\text{air}} g V \) (e.g., hot-air balloons).
16. In what direction does the buoyant force act?
Upward, along the vertical through \( B \), opposite to gravity.
17. How do you compute net force on a submerged object?
\( F_{\text{net}}=F_b-W =(\rho_f-\rho_{\text{obj}})gV_{\text{obj}} \).
18. What is the weight of displaced fluid for a floating wood log?
\( \rho_f g V_{\text{disp}}=\rho_{\text{log}} g V_{\text{log}}=m_{\text{log}} g \).
19. Why does a steel ship float?
The average density \( \bar{\rho}=\frac{m_{\text{steel}}+m_{\text{air}}}{V_{\text{hull}}} \) is below \( \rho_{\text{water}} \), so a displaced volume exists with \( F_b=W \).
20. How is the displaced volume measured in a laboratory?
Submerge the object and read the volume rise \( \Delta V \) in a graduated vessel; \( \Delta V=V_{\text{disp}} \).

20 Problems & Solutions

Problem 1: A cube of side \(0.2~\mathrm{m}\) and density \(600~\mathrm{kg\,m^{-3}}\) floats in water. What fraction of its height is submerged?
Solution: \( \frac{V_{\text{disp}}}{V_{\text{obj}}}=\frac{600}{1000}=0.6 \). Height submerged \(=0.6\times 0.2=0.12~\mathrm{m}\).
Problem 2: A sphere of radius \(0.1~\mathrm{m}\) is fully submerged in oil (\(\rho=850~\mathrm{kg\,m^{-3}}\)). Calculate the buoyant force.
Solution: \( V=\frac{4}{3}\pi(0.1)^3=4.19\times 10^{-3}\ \mathrm{m^3} \).
\( F_b=\rho g V=850\times 9.81\times 4.19\times 10^{-3}\approx 34.9~\mathrm{N} \).
Problem 3: A solid cylinder (\(r=0.05~\mathrm{m},\, L=1~\mathrm{m},\, \rho=700~\mathrm{kg\,m^{-3}}\)) floats in freshwater. Find the submerged length.
Solution: \( V_{\text{obj}}=\pi r^{2}L=\pi(0.05)^2(1)=7.85\times 10^{-3}\ \mathrm{m^3} \).
Submerged fraction \(=\rho_{\text{obj}}/\rho_f=0.7 \Rightarrow h_{\text{sub}}=0.7L=0.70~\mathrm{m} \).
Problem 4: A block of wood \((0.5\times 0.3\times 0.2~\mathrm{m})\), \( \rho=600~\mathrm{kg\,m^{-3}} \), in water. Determine \( F_b \).
Solution: \( V_{\text{obj}}=0.5\cdot 0.3\cdot 0.2=0.03~\mathrm{m^3} \).
\( V_{\text{disp}}=(\rho_{\text{obj}}/\rho_w)V_{\text{obj}}=0.6\times 0.03=0.018~\mathrm{m^3} \).
\( F_b=1000\cdot 9.81\cdot 0.018\approx 1.77\times 10^{2}~\mathrm{N} \).
Problem 5: A steel ship displaces \(2000~\mathrm{m^3}\) of water. Find its buoyant force.
Solution: \( F_b=1000\cdot 9.81\cdot 2000=1.962\times 10^{7}\ \mathrm{N} \).
Problem 6: A metal cube (\(\rho=7800~\mathrm{kg\,m^{-3}}\), side \(0.1~\mathrm{m}\)) is fully submerged. Calculate the net force.
Solution: \( V=1.0\times 10^{-3}\ \mathrm{m^3} \). \( F_b=1000\cdot 9.81\cdot 10^{-3}=9.81~\mathrm{N} \).
\( W=7800\cdot 9.81\cdot 10^{-3}=76.5~\mathrm{N} \).
\( F_{\text{net}}=F_b-W\approx -66.7~\mathrm{N} \) (downward).
Problem 7: A submerged object weighs \(50~\mathrm{N}\) in air and \(30~\mathrm{N}\) in water. Find \( F_b \) and its volume.
Solution: \( F_b=50-30=20~\mathrm{N} \). \( V=\frac{F_b}{\rho_w g}=\frac{20}{1000\cdot 9.81}=2.04\times 10^{-3}\ \mathrm{m^3} \).
Problem 8: A hot-air balloon displaces \(500~\mathrm{m^3}\) of air (\(\rho=1.2~\mathrm{kg\,m^{-3}}\)). Find its buoyant lift.
Solution: \( F_b=1.2\cdot 9.81\cdot 500\approx 5.89\times 10^{3}\ \mathrm{N} \).
Problem 9: A boat has \( G \) above \( B \). What does this imply?
Solution: If \( M \) remains above \( G \) so that \( GM>0 \), the boat is stable with a righting moment; if \( GM<0 \), it is unstable.
Problem 10: Derive the condition for neutral buoyancy.
Solution: \( F_b=W \Rightarrow \rho_f g V=\rho_{\text{obj}} g V \Rightarrow \rho_{\text{obj}}=\rho_f \).
Problem 11: A wooden plank (\(\rho=600~\mathrm{kg\,m^{-3}}\)) floats with half its volume submerged. Verify.
Solution: Required fraction \(=\rho_{\text{obj}}/\rho_w=0.6\neq 0.5\). So the claim is false; \(60\%\) should be submerged.
Problem 12: A cube floats with \(0.4~\mathrm{m}\) submerged; side \(0.5~\mathrm{m}\). Find its density.
Solution: Fraction \(=0.4/0.5=0.8 \Rightarrow \rho_{\text{obj}}=0.8\,\rho_w=800~\mathrm{kg\,m^{-3}} \).
Problem 13: A cylinder sinks with net force \(100~\mathrm{N}\) downward. What is \( F_b \) if \( W=300~\mathrm{N} \)?
Solution: \( F_{\text{net}}=W-F_b \Rightarrow 100=300-F_b \Rightarrow F_b=200~\mathrm{N} \).
Problem 14: A floating object displaces \(0.02~\mathrm{m^3}\) of water. What mass does it support?
Solution: \( m=\rho_w V=1000\times 0.02=20~\mathrm{kg} \).
Problem 15: Show that two objects with the same volume but different densities have different submerged depths.
Solution: For a prismatic float of height \( H \): \( \frac{h_{\text{sub}}}{H}=\frac{\rho_{\text{obj}}}{\rho_f} \).
Problem 16: A submerged cube experiences \( F_b=50~\mathrm{N} \). What is \( \rho_f \) if \( V=5\times 10^{-3}~\mathrm{m^3} \)?
Solution: \( \rho_f=\frac{F_b}{gV}=\frac{50}{9.81\cdot 5\times 10^{-3}}\approx 1.02\times 10^{3}\ \mathrm{kg\,m^{-3}} \).
Problem 17: A submarine adjusts its buoyancy by pumping water. Explain.
Solution: Taking in water raises average density so \( W>F_b \) (descend); expelling water lowers it so \( W
Problem 18: Why is Archimedes’ principle valid for irregular shapes?
Solution: Hydrostatic pressure depends only on depth; integrating over the surface gives \( F_b=\rho_f g V_{\text{disp}} \) independent of shape.
Problem 19: Estimate \( GM \) for a barge if the center of buoyancy shifts laterally by \(0.1~\mathrm{m}\) at a heel of \(5^\circ\).
Solution: For small angles, \( BM\approx \frac{\Delta x}{\tan\theta} \approx \frac{0.1}{\tan(5^\circ)}\approx 1.15~\mathrm{m} \). Then \( GM=BM-BG \) once \( BG \) is specified.
Problem 20: A material of density \(500~\mathrm{kg\,m^{-3}}\) is placed in liquid of \( \rho=1200~\mathrm{kg\,m^{-3}} \). Will it float?
Solution: Yes. Submerged fraction \(=\frac{\rho_{\text{obj}}}{\rho_f}=\frac{500}{1200}=0.417 \) (about \(41.7\%\)).

Buoyant Forces and Archimedes’ Principle