Chapter 6: Bernoulli’s Equation
Course: Prep4Uni Fluid Mechanics 1
Chapter 1: Pressure
Chapter 2: Variation of Pressure with Depth
Chapter 3: Pressure Measurement
Chapter 4: Buoyant Forces & Archimedes’ Principle
Chapter 5: Fluid Dynamics
Chapter 6: Bernoulli’s Equation
Chapter 7: Applications of Fluid Dynamics
🚁Overview of Bernoulli’s Equation
From the mechanical-energy balance for an inviscid, incompressible, steady flow (with no pumps/turbines or heat transfer between two points), we obtain Bernoulli’s equation along a streamline:
\[ p + \frac{1}{2}\rho v^{2} + \rho g h = \text{constant (along a streamline)}. \]Two very useful forms are:
- Head form (divide by \(\rho g\)): \[\frac{p}{\rho g} + \frac{v^{2}}{2g} + h = \text{constant}.\]
- Stagnation pressure (Pitot tube): \[ p_{0} = p + \frac{1}{2}\rho v^{2}, \] where \(p_{0}\) is measured at the stagnation port (\(v \to 0\)).
Typical applications: Pitot tubes (velocity from \(p_{0}-p\)), Venturi meters (flow rate using \(A_{1}v_{1}=A_{2}v_{2}\) and \[ p_{1}-p_{2}=\frac{1}{2}\rho\!\left(v_{2}^{2}-v_{1}^{2}\right), \] ), and free-surface flows with elevation change.
Assumptions and limitations:
- Steady and incompressible flow; density \(\rho\) is constant.
- Inviscid along the streamline (friction/head losses negligible) and no shaft work between points.
- Valid strictly along a single streamline (for irrotational flow, it can hold everywhere).
- When losses are important, use the extended form with a head-loss term \(h_f\): \[\frac{p_{1}}{\rho g} + \frac{v_{1}^{2}}{2g} + h_{1} = \frac{p_{2}}{\rho g} + \frac{v_{2}^{2}}{2g} + h_{2} + h_{f}.\]
- Derive \(\;p + \frac{1}{2}\rho v^{2} + \rho g h = \text{constant}\;\) along a streamline from energy conservation.
- Solve problems involving coupled changes in height, pressure, and velocity.
- Identify when assumptions (steady, inviscid, incompressible, no shaft work) are valid and when loss terms \(h_f\) are required.
📖Contents
- Derivation of Bernoulli’s Equation
- Applications of Bernoulli’s Equation
- Assumptions & Limitations of Bernoulli’s Equation
- Worked Examples on Bernoulli’s Equation
- Practice Problems on Bernoulli’s Equation
- Key Formula Recap
🎯Learning Outcomes
- Derive Bernoulli’s equation
p + ½ρv² + ρgh = constantfrom energy conservation along a streamline. - Identify and distinguish between static pressure, dynamic pressure (
½ρv²), and hydrostatic head (ρgh). - Apply Bernoulli’s equation to Pitot‐tube measurements to determine flow velocity from stagnation and static pressures.
- Use Bernoulli’s equation together with continuity to solve Venturi‐meter flow‐rate problems.
- Account for changes in elevation (
h) and velocity (v) when applying Bernoulli’s equation between two points. - Recognize the key assumptions (steady, inviscid, incompressible flow; no energy losses) and limitations of Bernoulli’s equation.
Table of Contents
6.1 Derivation of Bernoulli’s Equation
Energy conservation along a streamline (steady, incompressible, inviscid; no shaft work or heat transfer between stations).
Consider a fluid element of volume V that moves steadily from point 1 to point 2 along a streamline.
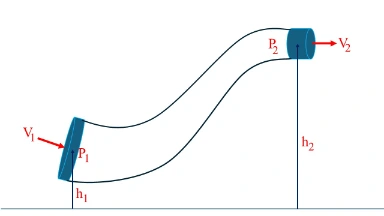
i) Work done by pressure forces
Upstream pressure does positive work \(p_{1}V\); downstream pressure does negative work \(-p_{2}V\).
Net work: \(W = V\,(p_{1}-p_{2})\).
ii) Change in kinetic energy
\(\Delta KE = \frac{1}{2}\,\rho V\,(v_{2}^{2}-v_{1}^{2})\).
iii) Change in potential energy
\(\Delta PE = \rho V g\,(h_{2}-h_{1})\).
iv) Mechanical energy balance
\(V\,(p_{1}-p_{2}) = \frac{1}{2}\rho V\,(v_{2}^{2}-v_{1}^{2}) + \rho V g\,(h_{2}-h_{1})\). Dividing by \(V\) and rearranging gives
Head form (divide by \(\rho g\)): \[ \frac{p}{\rho g} + \frac{v^{2}}{2g} + h = \text{constant}. \]
Assumptions
- Steady flow
- Incompressible fluid (constant density)
- Inviscid (negligible friction) and no shaft work or heat addition
- Applied along a single streamline (for irrotational flow, valid everywhere)
6.2 Applications of Bernoulli’s Equation
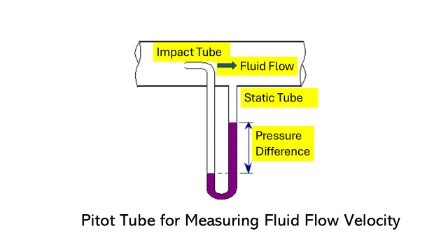
Pitot Tube
A Pitot tube measures stagnation pressure \(p_{0}\) where the local velocity is brought to zero. Applying Bernoulli between the free stream (1) and the stagnation point (0):
\[ p_{0} = p_{1} + \frac{1}{2}\rho v_{1}^{2} \quad\Rightarrow\quad v_{1} = \sqrt{\frac{2\,(p_{0}-p_{1})}{\rho}}. \]
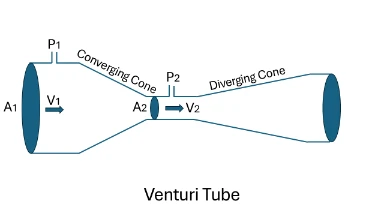
Venturi Meter
A Venturi contracts the flow from area \(A_{1}\) to \(A_{2}\), producing a pressure drop \(p_{1}-p_{2}\). Using continuity \(A_{1}v_{1}=A_{2}v_{2}\) and Bernoulli for a horizontal meter:
6.3 Assumptions & Limitations
- Inviscid: Viscous losses neglected; otherwise add head loss \(h_{f}\) to the right-hand side.
- Steady: Properties independent of time between measurements.
- Incompressible: Density constant (good for liquids; for gases, small Mach number).
- No external work/heat: No pumps/turbines/heat transfer between the two points.
6.4 Worked Examples
Example 1 (Pitot in air). Air with \(\rho=1.2~\text{kg m}^{-3}\) gives a stagnation rise of \(p_{0}-p=1200~\text{Pa}\).
Solution: \(v=\sqrt{\frac{2(1200)}{1.2}}\approx 44.7~\text{m s}^{-1}\).
Example 2 (Venturi in water). \(A_{1}=0.05~\text{m}^{2}\), \(A_{2}=0.02~\text{m}^{2}\), \(p_{1}-p_{2}=5000~\text{Pa}\), \(\rho=1000~\text{kg m}^{-3}\).
Solution: \[ Q = A_{2} \sqrt{\frac{2(5000)}{1000}\;\frac{0.05^{2}}{0.05^{2}-0.02^{2}}} \approx 5.8\times 10^{-2}~\text{m}^{3}\!/\text{s}. \]
6.5 Practice Problems
Problem 1. A Pitot tube in water (\(\rho=1000~\text{kg m}^{-3}\)) reads \(\Delta p=2500~\text{Pa}\). Find \(v\).
Solution: \(v=\sqrt{\frac{2\Delta p}{\rho}}=\sqrt{\frac{2(2500)}{1000}}\approx 2.24~\text{m s}^{-1}\).
Problem 2. Air (\(\rho=1.2~\text{kg m}^{-3}\)) flows from a duct of diameter \(0.30~\text{m}\) into a \(0.15~\text{m}\) nozzle. Static pressures are equal. Given \(v_{1}=5~\text{m s}^{-1}\), find \(v_{2}\).
Solution: \(v_{2}=v_{1}\left(\frac{D_{1}}{D_{2}}\right)^{2}=5\left(\frac{0.30}{0.15}\right)^{2}=20~\text{m s}^{-1}\).
Problem 3. Water descends a vertical pipe; neglect velocity change. What is \(\Delta p\) per meter of drop?
Solution: From \(p+\rho g h=\text{constant}\), \(\Delta p/\Delta h=-\rho g\approx -9.81\times10^{3}~\text{Pa m}^{-1}\).
6.6 Key Formula Recap
| Formula | Use |
|---|---|
| \(p + \frac{1}{2}\rho v^{2} + \rho g h = \text{constant}\) | Mechanical-energy balance along a streamline |
| \(v = \sqrt{\frac{2\,(p_{0}-p)}{\rho}}\) | Pitot-tube speed from dynamic pressure |
| \(Q = A_{2}\sqrt{\frac{2\,(p_{1}-p_{2})}{\rho}\;\frac{A_{1}^{2}}{A_{1}^{2}-A_{2}^{2}}}\) | Venturi meter flow rate (horizontal) |
Proceed to: Chapter 7: Applications of Fluid Dynamics
Return to: Prep4Uni Fluid Mechanics 1
📝EXERCISES
25 Questions & Answers on Bernoulli’s Equation
1. What is Bernoulli’s equation for steady incompressible flow?
Along a streamline for an inviscid, steady, incompressible flow: \[ p + \frac{1}{2}\rho v^{2} + \rho g h = \text{constant}. \]
2. What does the term \( \frac{1}{2}\rho v^{2} \) represent?
The dynamic pressure (kinetic energy per unit volume). It is the pressure rise obtained if the local velocity is isentropically reduced to zero.
3. What is the physical meaning of \( \rho g h \)?
The elevation (hydrostatic) term: gravitational potential energy per unit volume relative to a datum.
4. Under what assumptions is Bernoulli’s equation valid?
Steady, incompressible, inviscid flow; no shaft work or heat transfer between the two stations; applied along a single streamline (or everywhere if the flow is irrotational).
5. What is stagnation pressure?
The pressure when the fluid is brought to rest isentropically: \[ p_{0} = p + \frac{1}{2}\rho v^{2}. \]
6. How do you compute speed from a Pitot–static reading?
With measured difference \(p_{0}-p\): \[ v = \sqrt{\frac{2\,(p_{0}-p)}{\rho}}. \]
7. What is the Venturi effect?
A constriction accelerates the flow and lowers static pressure. For a horizontal Venturi: \[ p_{1} + \frac{1}{2}\rho v_{1}^{2} = p_{2} + \frac{1}{2}\rho v_{2}^{2}, \qquad v_{2} > v_{1}. \]
8. State the continuity equation for incompressible flow.
\[ A_{1}v_{1} = A_{2}v_{2}. \]
9. How does elevation difference enter Bernoulli’s equation?
Through \( \rho g h \). If elevation increases by \(\Delta h\) and speed is unchanged, static pressure drops by \( \rho g \Delta h \).
10. Why can viscous losses be neglected in the basic form?
The inviscid assumption removes shear work and dissipation. For real pipes add a head-loss term \(h_{f}\) to the right-hand side.
11. How do we include pump or turbine work?
In head form: \[ \frac{p_{1}}{\rho g} + \frac{v_{1}^{2}}{2g} + h_{1} + h_{\text{pump}} = \frac{p_{2}}{\rho g} + \frac{v_{2}^{2}}{2g} + h_{2} + h_{f} + h_{\text{turbine}}. \]
12. Why apply Bernoulli along a streamline?
The integration constant can vary between streamlines in rotational flows; along a single streamline the energy balance is unique.
13. How is Bernoulli modified for compressible flows?
Use the compressible form: \[ \int \frac{dp}{\rho} + \frac{1}{2}v^{2} + g h = \text{constant}. \]
14. What is dynamic head?
\( v^{2}/(2g) \). Its pressure equivalent is \( (1/2)\rho v^{2} \).
15. What is static head?
\( p/(\rho g) + h \): pressure head plus elevation head (potential energy terms).
16. How does a Pitot–static tube measure velocity?
Pitot port senses \(p_{0}\); side ports sense \(p\). The difference \(p_{0}-p\) gives \(v\) via Bernoulli.
17. What is total head?
\[ H = \frac{p}{\rho g} + \frac{v^{2}}{2g} + h, \] constant along a streamline for ideal flow (decreases by \(h_{f}\) in real pipes).
18. Why does pressure drop in a nozzle?
As area decreases, continuity raises \(v\); Bernoulli then requires \(p\) to fall so the sum \(p + (1/2)\rho v^{2}\) remains balanced (for constant \(h\)).
19. What happens if the assumptions are violated?
Predictions deviate. Include \(h_{f}\) for friction, unsteady terms for transient flow, or use the compressible integral for gases at higher Mach number.
20. How can Bernoulli help explain airfoil lift?
Higher speed over the upper surface implies lower pressure than below, producing a net upward force, in concert with curvature and circulation.
21. What is the role of potential energy?
The term \( \rho g h \) accounts for work against gravity; raising a streamline by \( \Delta h \) requires a reduction in \(p\) or \(v\).
22. How is Bernoulli obtained from work–energy?
Equate pressure work and weight work to the change in kinetic energy of a material element; divide by volume to obtain the per-unit-volume relation.
23. Why is Bernoulli not valid across a shock?
Shocks are irreversible and strongly compressible; dissipation converts mechanical energy to internal energy.
24. What is stagnation enthalpy?
\( h_{0} = h + v^{2}/2 \) (per unit mass). In adiabatic, no-work flow \(h_{0}\) is constant along a streamline.
25. How is Bernoulli used in Venturi measurement?
Measure \(p_{1}-p_{2}\) between inlet and throat, then use \[ Q = A_{2}\sqrt{ \frac{2\,(p_{1}-p_{2})}{\rho}\,\frac{A_{1}^{2}}{A_{1}^{2}-A_{2}^{2}} }, \] derived from Bernoulli plus \(A_{1}v_{1}=A_{2}v_{2}\).
25 Problems & Solutions on Bernoulli’s Equation
Problem 1. A Pitot tube in air (\(\rho=1.2~\text{kg m}^{-3}\)) records \(\Delta p=800~\text{Pa}\). Find \(v\).
Solution. \( v=\sqrt{\frac{2\Delta p}{\rho}}=\sqrt{\frac{2\times800}{1.2}} \approx 36.5~\text{m s}^{-1}. \)
Problem 2. Venturi with \(A_{1}/A_{2}=4\). If \(v_{2}=8~\text{m s}^{-1}\), find \(v_{1}\) and the predicted \(\Delta p\) (water).
Solution. \( v_{1}=(A_{2}/A_{1})v_{2}=2~\text{m s}^{-1}. \) Then \( \Delta p = p_{1}-p_{2} = \frac{1}{2}\rho\,(v_{2}^{2}-v_{1}^{2}) = \frac{1}{2}(1000)(64-4) = 3.0\times10^{4}~\text{Pa}. \)
Problem 3. Vertical pipe with constant velocity. Find \(\Delta p\) over \(\Delta h=5~\text{m}\) rise (water).
Solution. \( \Delta p = -\rho g \Delta h = -1000\times9.81\times5 = -4.91\times10^{4}~\text{Pa}. \)
Problem 4. Horizontal Venturi: \(A_{1}=0.10~\text{m}^{2}\), \(A_{2}=0.050~\text{m}^{2}\), \(p_{1}-p_{2}=2000~\text{Pa}\) (water). Find \(Q\).
Solution. \[ Q = A_{2}\sqrt{\frac{2\Delta p}{\rho}\frac{A_{1}^{2}}{A_{1}^{2}-A_{2}^{2}}} = 0.050\sqrt{\frac{2\times2000}{1000}\frac{0.10^{2}}{0.10^{2}-0.05^{2}}} \approx 1.15\times10^{-1}~\text{m}^{3}\!/\text{s}. \]
Problem 5. Air (\(\rho=1.18\)) at \(15~\text{m s}^{-1}\). Find dynamic pressure and stagnation rise.
Solution. \( q=\frac{1}{2}\rho v^{2}=0.5\times1.18\times15^{2}=132~\text{Pa}. \) Stagnation pressure \(=p+q\).
Problem 6. Water flows from diameter \(0.20~\text{m}\) into \(0.10~\text{m}\). If \(v_{1}=3~\text{m s}^{-1}\), find \(v_{2}\).
Solution. Area ratio \(=(0.20/0.10)^{2}=4\Rightarrow v_{2}=12~\text{m s}^{-1}\).
Problem 7. Pitot–static tube in water shows \(p_{0}-p=5000~\text{Pa}\). Find \(v\).
Solution. \( v=\sqrt{\frac{2\times5000}{1000}}=3.16~\text{m s}^{-1}. \)
Problem 8. Oil (\(\rho=850\)) in a Venturi gives \(\Delta p=1500~\text{Pa}\) with \(A_{1}/A_{2}=3\). Express \(Q\) in terms of \(A_{2}\).
Solution. \[ Q = A_{2}\sqrt{\frac{2\times1500}{850}\frac{3^{2}}{3^{2}-1}} \approx A_{2}\sqrt{3.529\times1.125}\approx 2.0\,A_{2}. \]
Problem 9. In a horizontal pipe, speed rises from \(4\) to \(6~\text{m s}^{-1}\) while \(\Delta p=800~\text{Pa}\). Is Bernoulli satisfied?
Solution. Required \(\Delta p=\frac{1}{2}\rho(6^{2}-4^{2})=10\,000~\text{Pa}\). Since \(800\ll10\,000\), there are significant losses or measurement error.
Problem 10. Orifice \(2~\text{m}\) below a free surface. Find \(v\).
Solution. \( v=\sqrt{2gh}=\sqrt{2\times9.81\times2}=6.26~\text{m s}^{-1}. \)
Problem 11. Water Venturi with \(A_{1}/A_{2}=4\) and \(\Delta p=2500~\text{Pa}\). Find \(v_{1}\).
Solution. \[ \Delta p=\frac{1}{2}\rho v_{1}^{2}\left[\left(\frac{A_{1}}{A_{2}}\right)^{2}-1\right] \Rightarrow v_{1}=\sqrt{\frac{2\times2500}{1000\,(16-1)}}=0.577~\text{m s}^{-1}. \]
Problem 12. Total pressure at 1 exceeds that at 2 by \(1000~\text{Pa}\). Find head loss \(h_{f}\) (water).
Solution. \( h_{f}=\Delta p/(\rho g)=1000/(1000\times9.81)=0.102~\text{m}. \)
Problem 13. Pipeline rises \(10~\text{m}\) with negligible velocity change. Compute \(\Delta p\) (water).
Solution. \( \Delta p=-\rho g \Delta h=-9.81\times10^{4}~\text{Pa}. \)
Problem 14. Air (\(\rho=1.20\)) at \(20~\text{m s}^{-1}\). Find dynamic pressure.
Solution. \( q=\frac{1}{2}\rho v^{2}=0.5\times1.20\times400=240~\text{Pa}. \)
Problem 15. Nozzle accelerates water from \(5\) to \(15~\text{m s}^{-1}\). What static pressure drop is needed (horizontal)?
Solution. \( \Delta p=\frac{1}{2}\rho(15^{2}-5^{2})=1.0\times10^{5}~\text{Pa}. \)
Problem 16. Why is Bernoulli not valid inside a boundary layer?
Solution. Strong viscous shear and dissipation violate the inviscid assumption; an \(h_{f}\) term is required.
Problem 17. Open-channel form with flow depth \(y\).
Solution. For a free surface \(p\approx p_{\text{atm}}\): \[ y + \frac{v^{2}}{2g} + \frac{p}{\rho g} = \text{constant}. \]
Problem 18. A tank discharges to atmosphere. At a point \(5~\text{m}\) below the free surface, what is the gauge pressure?
Solution. \( p=\rho g \Delta h = 1000\times9.81\times5 = 4.91\times10^{4}~\text{Pa}. \)
Problem 19. A meter shows static head \(10~\text{m}\) and stagnation head \(12~\text{m}\) (water). Find \(v\).
Solution. Velocity head \(=2~\text{m}\) ⇒ \( v=\sqrt{2g\times2}=6.26~\text{m s}^{-1}. \)
Problem 20. Include hydraulic losses in head form.
Solution. \[ \frac{p_{1}}{\rho g}+\frac{v_{1}^{2}}{2g}+h_{1} = \frac{p_{2}}{\rho g}+\frac{v_{2}^{2}}{2g}+h_{2} + h_{f}. \]
Problem 21. A jet exits vertically downward at \(5~\text{m s}^{-1}\) from height \(10~\text{m}\) above a plate. Estimate impact gauge pressure (neglect losses).
Solution. \( p=\rho g(10) + \frac{1}{2}\rho(5^{2}) \approx 9.81\times10^{4} + 1.25\times10^{3} \approx 1.00\times10^{5}~\text{Pa}. \)
Problem 22. Venturi with \(A_{2}=\frac{1}{2}A_{1}\). Express \(\Delta p\) in terms of \(v_{1}\) (horizontal liquid).
Solution. \( v_{2}=2v_{1} \Rightarrow \Delta p = \frac{1}{2}\rho(4v_{1}^{2}-v_{1}^{2}) = \frac{3}{2}\rho v_{1}^{2}. \)
Problem 23. Why must points lie on the same streamline for Bernoulli?
Solution. In rotational flow the energy constant differs across streamlines; mixing points from different streamlines gives an inconsistent balance.
Problem 24. Air at \(20^{\circ}\text{C}\) with \(\rho\approx1.204\) flows at \(10~\text{m s}^{-1}\). Find the dynamic pressure.
Solution. \( q=\frac{1}{2}\rho v^{2}=0.5\times1.204\times100=60.2~\text{Pa}. \)
Problem 25. Diffuser expands from \(D_{1}=0.05~\text{m}\) to \(D_{2}=0.10~\text{m}\). If \(p_{1}-p_{2}=1000~\text{Pa}\) (water), find \(v_{1}\) (horizontal).
Solution. Area ratio \(=(D_{1}/D_{2})^{2}=1/4\Rightarrow v_{2}=v_{1}/4\). Then \[ \Delta p=\frac{1}{2}\rho\left(v_{1}^{2}-\left(\frac{v_{1}}{4}\right)^{2}\right) = \frac{15}{32}\rho v_{1}^{2} \Rightarrow v_{1}=\sqrt{\frac{32\,\Delta p}{15\,\rho}} \approx 5.16~\text{m s}^{-1}. \]
