Prepare for University Studies & Career Advancement

Fluid Dynamics

In this chapter we begin the study of fluids in motion. We will introduce streamlines, define the volumetric flow rate Q and mass flow rate ṁ, derive the continuity equation for incompressible flow, and contrast laminar and turbulent regimes.

  • Define and compute volumetric and mass flow rates.
  • Use the continuity equation (ρAv = constant) to relate changes in cross-sectional area to velocity.
  • Distinguish between laminar and turbulent flow qualitatively and quantitatively.

Prep4Uni Fluid Mechanics 1 Central course portal coordinating core fluid dynamics modules, kinematic relationships, and syllabus pathways.

Chapter 1: Pressure Establishes core static definitions of normal force per unit area, pressure units, and gauge vs. absolute scales.

📖 Contents

  1. Volumetric & Mass Flow Rates
  2. Continuity Equation
  3. Laminar vs. Turbulent Flow
  4. Worked Examples
  5. Practice Problems
  6. Key Formula Recap
  7. Comprehensive Practice Exercises

🎯 Learning Outcomes

  • Define volumetric flow rate (Q = dV/dt) and mass flow rate (ṁ = ρQ).
  • Compute Q and ṁ given cross-sectional area and velocity (or vice versa).
  • Apply the continuity equation (ρAv = constant) to relate changes in pipe (or channel) area to fluid velocity.
  • Interpret streamlines and understand their significance for steady, incompressible flow.
  • Distinguish between laminar and turbulent flow regimes using the Reynolds number (Re = ρvD/μ).
  • Estimate whether a given flow is laminar or turbulent based on typical critical Re values.

5.1 Volumetric & Mass Flow Rates

Volumetric flow rate Q represents the volume of fluid passing through a given cross section per unit time:

Q = dV / dt = A · v

where A is the cross-sectional area and v is average flow velocity.

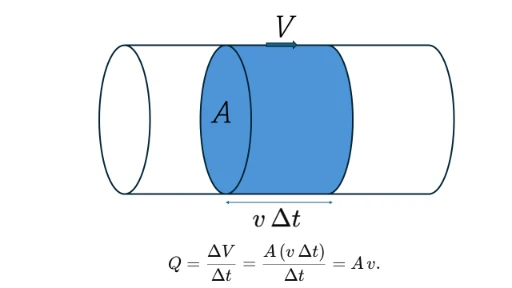
Volume Flow Rate
Volume Flow Rate

In time interval Δt, a fluid slug of length v · Δt sweeps past the cross section, producing displaced volume ΔV = A · (v · Δt), which simplifies directly to Q = ΔV / Δt = A · v.

Mass flow rate ṁ represents the total mass of fluid passing through the cross section per unit time:

ṁ = ρ · Q = ρ · A · v

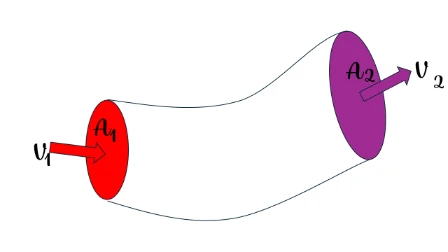
5.2 Continuity Equation

For steady, incompressible flow (constant density ρ), mass conservation dictates that volumetric flow rate Q remains uniform along any continuous streamline conduit:

A1 · v1 = A2 · v2

In general compressible flow systems, conservation of mass establishes the universal relation:

ρ · A · v = constant
Flow Through Varying Size Tube
Flow Through Varying Size Tube

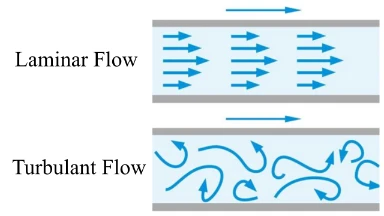
5.3 Laminar vs. Turbulent Flow

  • Laminar flow: Fluid moves smoothly in parallel layers or streamlines with minimal lateral mixing (low Reynolds number, Re < ≈ 2000 in internal pipe flow).
  • Turbulent flow: Highly chaotic, vortical motion characterized by rapid velocity fluctuations and strong momentum mixing (high Reynolds number, Re > ≈ 4000).
  • A transitional regime occurs between these two boundary limits (2000 ≤ Re ≤ 4000).
Laminar Flow and Turbulent Flow comparison
Laminar Flow and Turbulent Flow Comparison

5.4 Worked Examples

  1. Example 1: Water (ρ = 1000 kg/m3) flows through a pipe of diameter D = 0.10 m at average velocity v = 2 m/s. Compute volumetric and mass flow rates.
    Solution:
    A = π · (0.10 / 2)2 ≈ 7.854 × 10-3 m2.
    Q = A · v ≈ (7.854 × 10-3) × 2 = 1.571 × 10-2 m3/s (15.71 L/s).
    ṁ = ρ · Q = 1000 × (1.571 × 10-2) ≈ 15.71 kg/s.
  2. Example 2: The flow from Example 1 enters a pipe constriction of diameter D2 = 0.05 m. Find the new velocity.
    Solution:
    Applying continuity A1 · v1 = A2 · v2 ⇒ v2 = (A1 / A2) · v1 = (D1 / D2)2 · v1.
    v2 = (0.10 / 0.05)2 × 2 = (2)2 × 2 = 8.0 m/s.

5.5 Practice Problems

  1. Calculate Q and ṁ for oil (ρ = 850 kg/m3) flowing at 1.5 m/s in a 0.08 m diameter pipe.
    Solution:
    A = π · (0.08 / 2)2 ≈ 5.027 × 10-3 m2.
    Q = A · v = 5.027 × 10-3 × 1.5 ≈ 7.54 × 10-3 m3/s.
    ṁ = ρ · Q = 850 × 7.54 × 10-3 ≈ 6.41 kg/s.
  2. Water flows at 3 L/s through a nozzle; if exit diameter is 1 cm (0.01 m), find exit velocity.
    Solution:
    Q = 3 L/s = 0.003 m3/s.
    A = π · (0.01 / 2)2 ≈ 7.854 × 10-5 m2.
    v = Q / A = 0.003 / (7.854 × 10-5) ≈ 38.2 m/s.
  3. Estimate the Reynolds number for flow in Example 1 (water at 2 m/s in 0.10 m pipe, μ = 1.0 × 10-3 Pa·s) and determine the flow regime.
    Solution:
    Re = (ρ · v · D) / μ = (1000 × 2 × 0.10) / (1.0 × 10-3) = 200 000.
    Since Re = 200 000 >> 4000, the flow is fully turbulent.

5.6 Key Formula Recap

FormulaDescription
Q = A · vVolumetric flow rate equation
ṁ = ρ · Q = ρ · A · vMass flow rate equation
A1 · v1 = A2 · v2Incompressible flow continuity relationship
Re = (ρ · v · D) / μReynolds number evaluating flow regime transition

Interactive Continuity & Reynolds Number Simulator

Adjust inlet velocity (v1), inlet diameter (D1), constriction diameter (D2), and dynamic viscosity (μ) to observe flow acceleration and Reynolds number profile evolution across timeline steps.

Outlet Velocity (v2): 8.00 m/s
Reynolds Number (Re2): 400,000 (TURBULENT)

Interactive Fluid Kinematics Concept Toggles

Click each section below to toggle detailed explanations on flow field kinematics and continuity fundamentals.

Why does mass flow rate remain strictly constant along a closed conduit for steady flow?
By the Law of Conservation of Mass, fluid mass cannot accumulate or dissipate inside a rigid control volume under steady-state conditions. Consequently, the mass entering per second must equal the mass exiting per second (ṁ = ρ1A1v1 = ρ2A2v2).
What physical ratio does the dimensionless Reynolds number (Re = ρvD/μ) represent?
The Reynolds number represents the ratio of inertial fluid forces (ρv2) to internal viscous shearing forces (μv/D). High values indicate inertial dominance leading to turbulent mixing, whereas low values signify viscous dominance maintaining smooth laminar streamlines.
How do streamlines, streaklines, and pathlines differ in unsteady fluid motion?
In steady flow, streamlines, streaklines, and pathlines are completely identical. In unsteady flow: streamlines are instantaneous velocity tangent curves; pathlines trace the actual trajectory of a single particle over time; and streaklines join all particles that passed through a single injection point.

Frequently Asked Questions

Can fluid pass across a streamline in steady-state flow?

No. By definition, velocity vectors are everywhere tangent to streamlines, so there is zero normal velocity component across a streamline boundary.

Why does narrowing a garden hose nozzle increase water stream velocity?

By the incompressible continuity equation (v2 = v1 · A1 / A2), reducing nozzle exit area A2 forces water velocity v2 to increase proportionally to maintain volumetric flow rate.

What is the critical Reynolds number for internal pipe flow transition?

For smooth circular pipe flow, Re < 2000 is generally laminar, 2000 ≤ Re ≤ 4000 is transitional, and Re > 4000 is fully turbulent.

📝 Comprehensive Practice Module

Section 1: Foundational Core Assessment

  1. What is volumetric flow rate?
    Answer: The volume of fluid passing through a cross-sectional area per unit time: Q = A · v.
  2. What is mass flow rate?
    Answer: The mass of fluid passing through a cross section per unit time: ṁ = ρ · Q = ρ · A · v.
  3. State the continuity equation for incompressible fluid flow.
    Answer: A1 · v1 = A2 · v2 (or Q = constant along a streamline).
  4. How do streamlines represent fluid motion?
    Answer: Streamlines are continuous curves everywhere tangent to local velocity vectors in steady flow.
  5. How does fluid velocity change when conduit cross-sectional area decreases?
    Answer: Velocity increases inversely with area to maintain constant volumetric flow rate.
  6. Define laminar flow.
    Answer: Smooth, organized fluid motion moving in parallel layers with minimal lateral mixing (typically Re < 2000).
  7. Define turbulent flow.
    Answer: Chaotic fluid motion with cross-current velocity fluctuations, eddies, and rapid mixing (typically Re > 4000).
  8. Define the Reynolds number equation for internal pipe flow.
    Answer: Re = (ρ · v · D) / μ, where D is pipe hydraulic diameter and μ is dynamic viscosity.
  9. What does a pipe Reynolds number Re < 2000 indicate?
    Answer: Laminar flow regime.
  10. What does a pipe Reynolds number Re > 4000 indicate?
    Answer: Fully turbulent flow regime.

Section 2: Analytical & Conceptual Analysis

  1. What is the primary SI unit for volumetric flow rate Q?
    Answer: Cubic meters per second (m3/s).
  2. What is the primary SI unit for mass flow rate ṁ?
    Answer: Kilograms per second (kg/s).
  3. How is average velocity computed when volumetric flow rate Q and diameter D are known?
    Answer: v = Q / A = 4 · Q / (π · D2).
  4. Why is the product ρ · A · v constant along a closed conduit in steady flow?
    Answer: Mass conservation dictates that total fluid mass entering per second must equal total fluid mass exiting per second.
  5. What key characteristic distinguishes steady flow from unsteady flow?
    Answer: In steady flow, fluid properties (velocity, pressure, density) at any fixed point remain constant over time.
  6. Convert a volumetric flow rate of 10 L/min into m3/s.
    Answer: 10 L/min = (10 × 10-3 m3) / 60 s ≈ 1.667 × 10-4 m3/s.
  7. How does fluid density affect mass flow rate for a fixed volumetric flow rate?
    Answer: Mass flow rate scales directly with density (ṁ = ρ · Q); higher density increases ṁ.
  8. What is the physical significance of a streamtube in fluid kinematics?
    Answer: A streamtube is a tubular surface formed by a collection of streamlines through which zero fluid mass passes across the outer boundary wall.
  9. How is the continuity equation expressed for 3D compressible flow?
    Answer: ∂ρ / ∂t + ∇ · (ρv) = 0.

Section 3: Computational & Numerical Exercises

  1. Water (ρ = 1000 kg/m3) flows at 2 m/s in a 0.10 m diameter pipe. Calculate Q and ṁ.
    Solution:
    A = π · (0.10)2 / 4 ≈ 7.854 × 10-3 m2.
    Q = A · v = 7.854 × 10-3 × 2 ≈ 1.571 × 10-2 m3/s.
    ṁ = 1000 × 1.571 × 10-2 ≈ 15.71 kg/s.
  2. Oil (ρ = 850 kg/m3) flows at 1.5 m/s in a 0.08 m diameter pipe. Compute Q and ṁ.
    Solution:
    A = π · (0.08)2 / 4 ≈ 5.027 × 10-3 m2.
    Q = 5.027 × 10-3 × 1.5 ≈ 7.54 × 10-3 m3/s.
    ṁ = 850 × 7.54 × 10-3 ≈ 6.41 kg/s.
  3. A pipe tap delivers 10 L/min of water. If its nozzle diameter is 1 cm (0.01 m), find the exit velocity.
    Solution:
    Q = 10 × 10-3 / 60 ≈ 1.667 × 10-4 m3/s.
    A = π · (0.01)2 / 4 ≈ 7.854 × 10-5 m2.
    v = Q / A = 1.667 × 10-4 / (7.854 × 10-5) ≈ 2.122 m/s.
  4. Water flow in a pipe with cross-sectional area 0.02 m2 enters a constriction of area 0.005 m2. If initial velocity is 3 m/s, calculate the constriction velocity.
    Solution:
    v2 = (A1 / A2) · v1 = (0.02 / 0.005) × 3 = 4 × 3 = 12.0 m/s.
  5. A mass flow rate of 20 kg/s passes through a duct of cross-sectional area 0.1 m2 filled with air (ρ = 1.2 kg/m3). Find air velocity.
    Solution:
    Q = ṁ / ρ = 20 / 1.2 ≈ 16.67 m3/s.
    v = Q / A = 16.67 / 0.1 = 166.7 m/s.
  6. Compute average flow velocity when Q = 0.05 m3/s passes through a circular pipe of diameter 0.2 m.
    Solution:
    A = π · (0.2)2 / 4 ≈ 0.03142 m2.
    v = Q / A = 0.05 / 0.03142 ≈ 1.59 m/s.
  7. Find the Reynolds number for water (ρ = 1000 kg/m3, μ = 1.0 × 10-3 Pa·s) flowing at 1 m/s through a 0.05 m diameter pipe.
    Solution:
    Re = (ρ · v · D) / μ = (1000 × 1 × 0.05) / (1.0 × 10-3) = 50 000 (turbulent).
  8. A streamtube narrows from area 0.03 m2 to 0.01 m2. If Q is constant at 0.06 m3/s, determine velocity in both sections.
    Solution:
    v1 = Q / A1 = 0.06 / 0.03 = 2.0 m/s.
    v2 = Q / A2 = 0.06 / 0.01 = 6.0 m/s.
  9. If gasoline (ρ = 740 kg/m3) flows at 4 m/s in a 0.1 m2 conduit, calculate mass flow rate ṁ.
    Solution:
    Q = A · v = 0.1 × 4 = 0.4 m3/s.
    ṁ = ρ · Q = 740 × 0.4 = 296 kg/s.
  10. A pipe constriction reduces pipe diameter by half (D2 = 0.5 · D1). By what factor does fluid velocity increase?
    Solution:
    v2 / v1 = (D1 / D2)2 = (1 / 0.5)2 = 4. Velocity increases by a factor of 4.
  11. Convert a water flow rate of 500 L/min in a conduit into mass flow rate ṁ in kg/s (ρ = 1000 kg/m3).
    Solution:
    Q = 500 × 10-3 / 60 ≈ 8.333 × 10-3 m3/s.
    ṁ = 1000 × (8.333 × 10-3) ≈ 8.33 kg/s.
  12. A fluid with ρ = 950 kg/m3 flows at Q = 0.02 m3/s in a 0.1 m diameter pipe. Compute Re given dynamic viscosity μ = 1.5 × 10-3 Pa·s.
    Solution:
    A = π · (0.1)2 / 4 ≈ 7.854 × 10-3 m2.
    v = Q / A = 0.02 / (7.854 × 10-3) ≈ 2.546 m/s.
    Re = (950 × 2.546 × 0.1) / (1.5 × 10-3) ≈ 161 247 (turbulent).
Last updated: 05 Aug 2026