Chapter 2: Variation of Pressure with Depth

Course: Prep4Uni Fluid Mechanics 1

Chapter 1: Pressure
Chapter 2: Variation of Pressure with Depth
Chapter 3: Pressure Measurement
Chapter 4: Buoyant Forces & Archimedes’ Principle
Chapter 5: Fluid Dynamics
Chapter 6: Bernoulli’s Equation
Chapter 7: Applications of Fluid Dynamics

🚁Overview

Overview:
In a static (non‐moving) fluid of uniform density ρ, the pressure at a depth h below the free surface increases linearly with h. By performing a force‐balance on a fluid element, one arrives at the hydrostatic formula
p = p₀ + ρ g h,
where p₀ is the pressure at the free surface (often atmospheric).

📖Contents

Definition
SI Unit
Gauge Vs Absolute Pressure
Characteristics of Pressure in Fluids
Example Calculation
Key Formula Recap

🎯Learning Outcomes

Explain the concept of hydrostatic pressure and how it develops in a static fluid.
Derive the hydrostatic pressure equation p = p₀ + ρ g h using both a force‐balance on a fluid element and the differential form dp/dz = ρ g.
Apply the formula p = p₀ + ρ g h to compute absolute and gauge pressures at a given depth in fluids of uniform density.
Account for non‐atmospheric free‐surface pressure p₀ when calculating pressure in enclosed or pressurized containers.
Solve hydrostatic‐pressure problems, including finding the depth corresponding to a specified pressure and determining pressure differences between two depths.
Use the differential relation dp/dz = ρ g to generalize pressure variation in fluids with depth (including variable density cases).

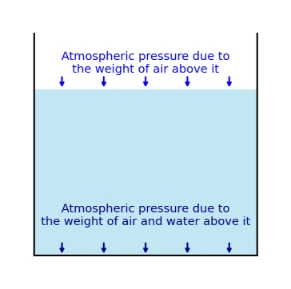
2.1 Concept of Hydrostatic Pressure

• In a fluid at rest, any small element feels force on its top and bottom faces due to the surrounding pressure, plus its own weight.
• Because pressure transmits equally in all directions at a point, a simple vertical slice (column) of fluid suffices to derive the depth‐dependence.

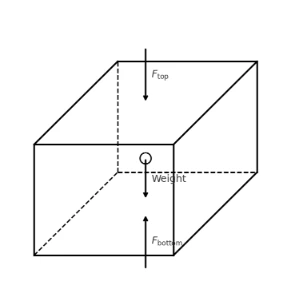
2.2 Derivation by Force Balance on a Fluid Element

Consider a right‐prism of fluid of cross‐sectional area A and height h:

Top face pressure: p₀ → downward force on prism: F_top = p₀ A
Bottom face pressure: p → upward reaction on prism: F_bottom = p A
Weight of fluid: W = ρ g A h acting downward

Static equilibrium ⇒ F_bottom – F_top – W = 0. Thus:

p A – p₀ A – ρ g A h = 0
⟹ p = p₀ + ρ g h

Fbottom=Ftop+Weight — F at bottom=F at top + Weight

2.3 Differential Derivation

Alternatively, consider an infinitesimal layer of thickness dz at depth z:
• Pressure on bottom: p(z + dz)
• Pressure on top: p(z)
• Weight of layer: dW = ρ g A dz

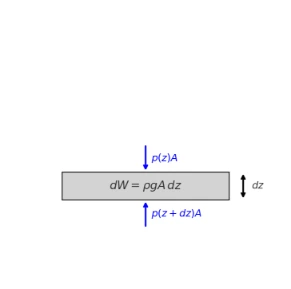
Force balance ⇒ p(z + dz) A – p(z) A – ρ g A dz = 0
Divide by A and take dz → 0:

dp/dz = ρ g
Integrate from surface (z = 0, p = p₀) to depth h:

∫ₚ_₀ᵖ dp = ∫₀ʰ ρ g dz → p – p₀ = ρ g h → p = p₀ + ρ g h

2.4 Free‐Surface vs. Gauge Pressure

Absolute pressure: p = p₀ + ρ g h, with p₀ = absolute free‐surface pressure (often 1 atm).
Gauge pressure: p_gauge ≡ p – p₀ = ρ g h.

In many applications, one only needs p_gauge = ρ g h, since p₀ is known or cancels out.

2.5 Worked Examples

Example 1: Depth = 5 m in fresh water (ρ=1000 kg/m³, g=9.81 m/s²). Find absolute pressure.

Solution:
p = 1.013×10⁵ Pa + (1000)(9.81)(5) ≈ 1.062×10⁵ Pa.

Example 2: Oil of density ρ=850 kg/m³ is used in a gauge of a hydraulic press. What gauge pressure corresponds to 3 m depth?

Solution:
p_gauge = ρ g h = 850 × 9.81 × 3 ≈ 2.50×10⁴ Pa (≈25 kPa).

2.6 Practice Problems & Solutions

Problem 1: Calculate the depth at which p_gauge = 150 kPa in seawater (ρ = 1025 kg/m³).

Solution:
Gauge pressure in a fluid: p_gauge = ρ g h
⇒ h = p_gauge / (ρ g) = (1.50×10⁵ Pa) / (1025 kg/m³ × 9.81 m/s²)
⇒ h ≈ 14.9 m

Problem 2: Find the absolute pressure 12 m below the surface if p₀ = 120 kPa (e.g. in a pressurized tank).

Solution:
Absolute pressure at depth: p = p₀ + ρ g h
Assuming water (ρ = 1000 kg/m³, g = 9.81 m/s²):
p = 1.20×10⁵ Pa + (1000×9.81×12) Pa = 1.20×10⁵ + 1.18×10⁵ Pa
⇒ p ≈ 2.38×10⁵ Pa

Problem 3: A dam wall at depth h experiences force F = p A. Express F as a function of h, ρ, and A.

Solution:
At depth h, absolute pressure is p = p₀ + ρ g h. If we take gauge force on the wall (ignoring atmospheric), then p = ρ g h. Thus
F = p A = (ρ g h) A.

Problem 4: Derive the pressure difference between two depths in a fluid with variable density ρ(z) by integrating dp/dz = ρ(z) g.

Solution:
Starting from the differential form:
dp = ρ(z) g dz.
Integrate from depth z₁ (pressure p₁) to z₂ (pressure p₂):

∫_p₁^p₂ dp = ∫_z₁^z₂ ρ(z) g dz
⇒ p₂ − p₁ = g ∫_z₁^z₂ ρ(z) dz.

2.7 Key Formula Recap

Formula	Description
`p – p₀ = ρ g h`	Increase in pressure below free surface
`p = p₀ + ρ g h`	Total (absolute) pressure at depth
`p_gauge = ρ g h`	Gauge pressure (relative to surface)
`dp/dz = ρ g`	Differential form for hydrostatic equilibrium

Proceed to: Chapter 3: Pressure Measurement

Return to: Prep4Uni Fluid Mechanics 1

📝EXERCISES

25 Questions & Answers

1. What is hydrostatic pressure?

Pressure exerted by a fluid at rest due to the weight of the fluid above; mathematically p = p₀ + ρ g h.

2. State the hydrostatic pressure equation.

p = p₀ + ρ g h, where p₀ is free‐surface pressure, ρ density, g gravity, h depth.

3. How is gauge pressure defined in a fluid?

Gauge pressure is the pressure above free‐surface pressure: p_gauge = ρ g h.

4. How is absolute pressure in a fluid expressed?

Absolute pressure includes atmospheric (or free‐surface) pressure: p_abs = p₀ + ρ g h.

5. What are the SI units of pressure?

The pascal (Pa), where 1 Pa = 1 N/m².

6. How does hydrostatic pressure vary with depth?

It increases linearly with depth: doubling h doubles ρ g h.

7. What is ρ in the hydrostatic equation?

The density of the fluid in kg/m³.

8. What is g in the hydrostatic equation?

The acceleration due to gravity, approximately 9.81 m/s² on Earth.

9. What does p₀ represent?

The pressure at the free surface (often atmospheric pressure).

10. What is the pressure at h = 0?

It equals the free‐surface pressure p₀.

11. Why is hydrostatic pressure isotropic?

Because in a static fluid pressure is transmitted equally in all directions at a point.

12. What differential equation describes hydrostatics?

dp/dz = ρ g, where z is depth coordinate.

13. How do you integrate the hydrostatic differential form?

Integrate dp = ρ g dz from 0 → h to obtain p – p₀ = ρ g h.

14. Does the formula apply to gases?

Only if gas density is effectively constant; otherwise one must account for variable ρ(z).

15. How is variable‐density fluid handled?

By integrating dp = ρ(z) g dz over the depth interval.

16. What is a manometer?

A device that measures pressure by the height difference of a liquid column.

17. How would you find depth for a given gauge pressure?

h = p_gauge / (ρ g).

18. At depth 10 m in water, what is gauge pressure?

ρ g h = 1000×9.81×10 ≈ 9.81×10⁴ Pa.

19. Why might p₀ be neglected?

When using gauge pressure, since p₀ is subtracted out.

20. How do you account for multiple fluid layers?

Sum contributions: p = p₀ + Σ ρ_i g h_i.

21. What is the significance of hydrostatic pressure in dam design?

It determines the force distribution on the dam wall as a function of depth.

22. How does temperature affect hydrostatic pressure?

Via density ρ(T); warmer fluid is less dense, reducing pressure gradient.

23. State Pascal’s law.

Pressure applied to an enclosed fluid is transmitted undiminished in all directions.

24. Why is hydrostatic pressure critical in submarine design?

To ensure hull strength withstands external pressure at operating depths.

25. What assumption underlies the simple hydrostatic equation?

That fluid density is uniform and g is constant over the depth considered.

25 Problems & Solutions

Problem 1: Calculate the gauge pressure at 8 m depth in fresh water (ρ=1000 kg/m³).
Solution:
p_gauge = ρ g h = 1000×9.81×8 ≈ 7.85×10⁴ Pa.
Problem 2: Find the depth at which gauge pressure is 200 kPa in oil (ρ=850 kg/m³).
Solution:
h = p_gauge/(ρ g) = 2.00×10⁵/(850×9.81) ≈ 24.0 m.
Problem 3: What is the absolute pressure 15 m below the surface if p₀=101 kPa?
Solution:
p = p₀ + ρ g h = 1.01×10⁵ + 1000×9.81×15 ≈ 2.57×10⁵ Pa.
Problem 4: A tank is pressurized at p₀=150 kPa. Find p at 5 m depth in water.
Solution:
p = 1.50×10⁵ + 1000×9.81×5 ≈ 1.99×10⁵ Pa.
Problem 5: In a U‐tube manometer with mercury (ρ=13 600 kg/m³), a fluid causes Δh=0.05 m. Find gauge pressure.
Solution:
p_gauge = ρ g Δh = 13600×9.81×0.05 ≈ 6.67×10³ Pa.
Problem 6: Two fluids, water (10 m) over oil (2 m, ρ=850 kg/m³). Find total p_gauge at bottom.
Solution:
p = 1000×9.81×10 + 850×9.81×2 ≈ 1.18×10⁵ + 1.67×10⁴ ≈ 1.35×10⁵ Pa.
Problem 7: Calculate depth of a column of mercury that corresponds to a pressure of 760 mm Hg column (ρ=13 600 kg/m³).
Solution:
Note: 760 mm Hg column = 1 atmospheric pressure = 101300 Pa
h = p_gauge/(ρ g) with p_gauge = 101300 Pa → h ≈ 0.76 m (by definition).
Problem 8: Pressure at 20 m in seawater (ρ=1025 kg/m³).
Solution:
p_gauge = 1025×9.81×20 ≈ 2.01×10⁵ Pa.
Problem 9: Find depth for p_gauge=50 kPa in mercury (ρ=13 600 kg/m³).
Solution:
h = 5.0×10⁴/(13600×9.81) ≈ 0.37 m.
Problem 10: Derive p difference between z₁=2 m and z₂=7 m in water.
Solution:
Δp = ρ g (z₂–z₁) = 1000×9.81×5 = 4.91×10⁴ Pa.
Problem 11: A dam face area A=2 m² at depth h. Express force F.
Solution:
F = p_gauge A = ρ g h A.
Problem 12: If p₀=120 kPa and ρ varies linearly 800→1000 kg/m³ over 5 m, approximate p at 5 m.
Solution:
Approx ρ_avg=900 kg/m³ → p ≈1.20×10⁵+900×9.81×5 ≈1.64×10⁵ Pa.
Problem 13: Compute pressure just below surface (h→0).?
Solution:
Gazе pressure→0; absolute p→p₀.
Problem 14: A column of oil (ρ=850 kg/m³) 3 m high rests on water (ρ=1000). Find p at interface.
Solution:
p =1000×9.81×3 +850×9.81×3 ≈5.89×10⁴ Pa.
Problem 15: Convert 5 m water head to equivalent mercury head (ρHg=13600).
Solution:
h_Hg = (1000/13600)×5 ≈0.37 m.
Problem 16: Gas density negligible. At 10 m water, find p_abs if p₀=95 kPa.
Solution:
p =9.5×10⁴+1000×9.81×10 ≈1.48×10⁵ Pa.
Problem 17: In a pressurized vessel p₀=300 kPa, find gauge pressure at h=4 m fluid (ρ=1200).
Solution:
p_gauge =1200×9.81×4 ≈4.71×10⁴ Pa.
Problem 18: Sea level p₀=101 kPa, find depth where p_abs=201 kPa in water.
Solution:
ρ g h =1.00×10⁵ → h ≈10.2 m.
Problem 19: How high must water rise in a pitot tube if flow pressure is 1200 Pa?
Solution:
h =1200/(1000×9.81) ≈0.12 m.
Problem 20: For variable ρ(z)=1000+z (kg/m³), find p₂–p₁ between z₁=0 and z₂=2 m.
Solution:
Δp =g∫₀²(1000+z)dz=9.81[1000z+½z²]₀² ≈9.81(2000+2)=1.96×10⁴ Pa.
Problem 21: A cistern area 1 m² filled to 3 m. Compute total force on bottom.
Solution:
p_avg=ρ g h/2=1000×9.81×1.5≈1.47×10⁴ Pa
F=p_avg×A≈1.47×10⁴ N.
Problem 22: A fluid of ρ=1400 kg/m³ -> find depth for p_gauge=100 kPa.
Solution:
h=100000/(1400×9.81)≈7.3 m.
Problem 23: Pressure difference between 4 m and 9 m in oil (ρ=850 kg/m³).
Solution:
Δp=850×9.81×5≈4.17×10⁴ Pa.
Problem 24: Show that dividing by A removes area from hydrostatic equation.
Solution:
(pA–p₀A–ρ g A h)/A=0→p–p₀–ρ g h=0.
Problem 25: Why is hydrostatic pressure independent of container shape?
Solution:
Because p=ρ g h depends only on depth, not volume or shape.

Prepare for University Studies & Career Advancement

Variation of Pressure with Depth